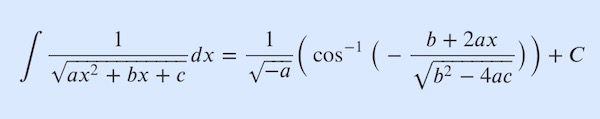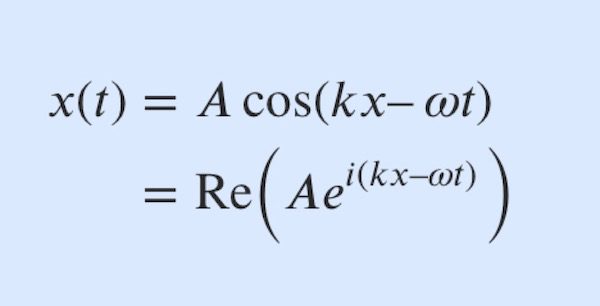BallPen.blog, 내 나이의 빛깔
BallPen 
벡터 미분 연산자를 이용한 일계 미분의 몇가지 곱셈 규칙을 알아 봐요. 일계 미분 곱셈 규칙 몇가지를 알아 봐요. 전자기학 등을 공부할 때 자주 등장하는 규칙들이에요. 참고로 몇가지 이계 미분 곱셈 규칙도 있으니 이것이 궁금하면 링크를 클릭하시기 바랍니다. 벡터 미분 연산자(또는 델연산자)가 사용된 일계 미분 곱셈 규칙은 다음과 같아요. 여기서 와 는 스칼라 함수이고 와 는 … Read more
역제곱 중심력이 작용할 때 행성 궤도가 갖는 에너지를 구해 봐요. 행성 궤도의 에너지 크기는 행성이 타원궤도를 갖는지 아니면 포물선궤도나 쌍곡선궤도를 갖는지에 따라 달라집니다. 그리고 행성 궤도를 알기 위해서는 이심율 을 구해야 하는데요. 이심율은 행성의 궤도 방정식으로도 구할 수 있지만 이 글에서 소개하는 궤도의 에너지 방정식을 통해 구할 수도 있어요. 궤도의 에너지 방정식은 다음과 같아요. 여기서 … Read more
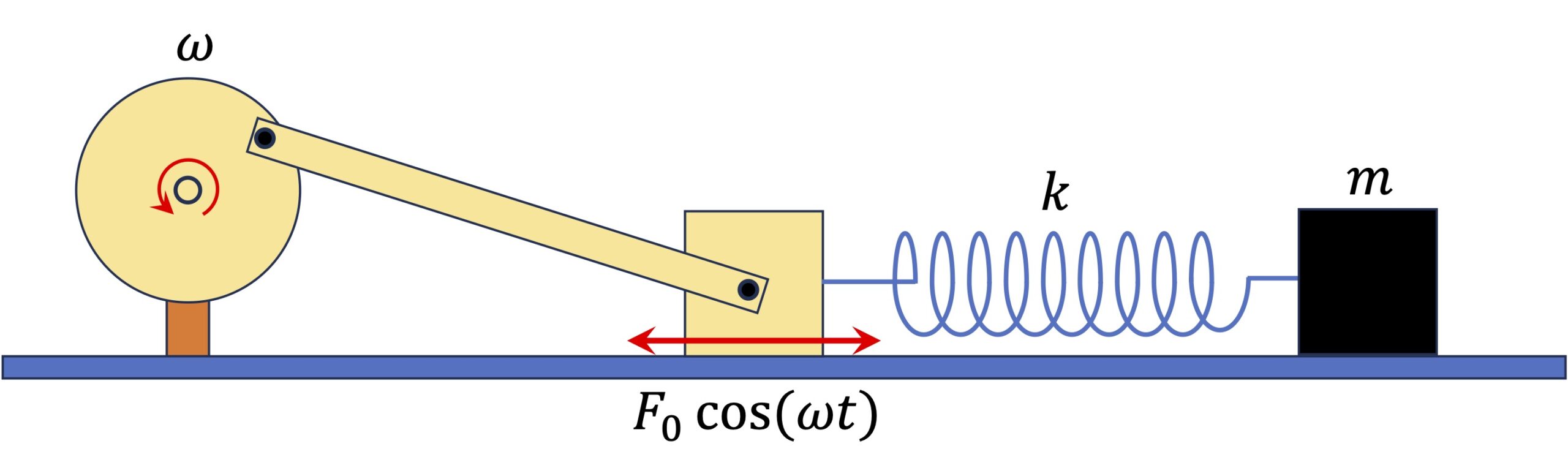
재미있는 적분 문제 하나를 풀어 보도록 해요. 과학을 하다보면 여러 적분 문제를 풀게 되는데요. 그중에서 아래 문제가 어떻게 풀어지게 되는지 구해보도록 해요. 이때 \(a<0\)으로 가정하겠습니다. \begin{align}\int{{1}\over{\sqrt{ax^2 + bx +c}}}dx = {1 \over{\sqrt{-a}}} \Big(\cos^{-1}\big(-{{b+2ax}\over{\sqrt{b^2 -4ac}}}\big)\Big) + C\end{align} 그리고 윗 식에서 대문자 \(C\)는 적분상수입니다. [풀이] \(P\)로 주어진 다음 적분을 풀어 봐요. \begin{align}\tag{1}P=\int{{1}\over{\sqrt{ax^2 + bx +c}}}dx\end{align} 먼저 위 … Read more
입자의 궤도방정식에 역제곱 중심력을 대입하면 타원궤도가 얻어짐을 알아 봐요. 케플러 제1법칙(Kepler’s 1st law of planetary motion)이란 태양을 한 초점으로 하는 타워궤도를 따라 행성이 공전한다는 법칙입니다. 따라서 이 법칙을 타원궤도의 법칙이라고도 불러요. 이 법칙은 입자의 궤도방정식에 역제곱 중심력을 대입하여 공전각도 \(\theta\)에 따른 입자의 궤도식을 구함으로써 명확이 입증할 수 있습니다. 그 결과는 다음 식으로 주어져요. \begin{align}\tag{D1}r = … Read more
중심력장 하에서 움직이는 입자의 궤도를 구하는 미분방정식을 알아 봐요. 입자의 궤도 방정식(differential equation of the orbit of a particle)이란 어떤 중심력(Central Force) 하에서 움직이는 입자가 무슨 궤도를 갖게 되는지를 구할 수 있는 미분방정식입니다. 이 방정식에 중심력을 대입하여 풀면 \(\theta\)의 함수로 원점으로부터 입자까지의 거리 \(r\)을 구할 수 있어요. 그래서 \(\theta\)의 범위에 따라 \(r\)의 값을 구한 후 … Read more
패러데이 법칙과 유도전기장에 대해 알아 봐요. 패러데이 법칙(Faraday’s law)이란 패러데이(Michael Faraday)가 발견한 전자기유도법칙으로 시간에 따라 변하는 자기장선속(magnetic flux)이 기전력을 생성한다는 법칙입니다. 이 법칙의 일반형은 다음과 같아요. \begin{align}\oint_c \vec E \cdot d \vec l = – {{d \Phi_B}\over{dt}}\end{align} 위 식에서 적분기호 밑의 \(c\)는 closed의 머리글자로 닫힌 경로를 뜻합니다. \(\Phi_B\)는 자기장 선속을 의미하고 이 자기장 선속이 시간에 … Read more
한번 흔들어진 진동자가 얼마나 오랫동안 진동을 유지할 수 있는가의 척도인 Q 인자에 대해 알아 봐요. Q 인자(quality factor)는 Q 인수, Q 값이라고도 불리는데요. 이 인자는 진동을 시작한 진동자가 얼마나 오랬동안 그 진동을 유지할 수 있는가의 척도입니다. 예를 들어, 공기 중 용수철에 매달린 물체를 당겼다가 놓으면 진동을 시작하는데요. 당연히 오랫동안 그대로 두면 공기저항력에 의해 진동이 멈추게 … Read more
사인과 코사인 곱을 한 주기에 걸쳐 적분해 봐요. 사인과 코사인 곱의 적분 계산을 위해서는 부분적분법을 사용하면 편리해요. 1. 부분적분법 부분적분법 공식은 다음과 같아요. \begin{align}\tag{1}\int_a^b u {v}’ d \theta = \Big[uv\Big]_a^b – \int_a^b u’ v d\theta \end{align} 2. 사인과 코사인 곱의 적분 이제 사인과 코사인 곱의 적분을 알아 봐요. 즉, 다음의 적분을 계산해 보자는 거에요. \begin{align}\tag{2}\int_0^{2\pi} … Read more
한 주기에 걸친 코사인 제곱 함수의 적분을 계산해 봐요. 코사인 제곱 함수 적분 방법을 알아 봐요. 즉, 다음의 적분을 계산해 보자는 거에요. \begin{align}\tag{1}\int_0^{2\pi} \cos^2 \theta d \theta\end{align} 이 계산을 위해서는 코사인 두배각 공식을 적용하는게 좋아요. 그 공식은 다음과 같아요. \begin{align}\tag{2}\cos 2 \theta = 2 \cos^2 \theta -1\end{align} 위 (2)식을 \(\cos^2 \theta\)에 대해 풀면 다음과 같아요. … Read more
한 주기에 걸친 사인 제곱 함수의 적분을 계산해 봐요. 사인 제곱 함수 적분 방법을 알아 봐요. 즉 다음의 적분을 계산해 보자는 거에요. \begin{align}\tag{1}\int_0^{2 \pi} \sin^2 \theta d\theta\end{align} 이 계산을 위해서는 코사인 두배각 공식을 이용하는게 좋아요. 코사인 두배각 공식은 다음과 같아요. \begin{align}\tag{2}\cos2\theta = 1- 2 \sin^2 \theta\end{align} 위 (2)식을 \(\sin^2 \theta\)에 대해 풀면 다음과 같아요. \begin{align}\tag{3}\sin^2 … Read more