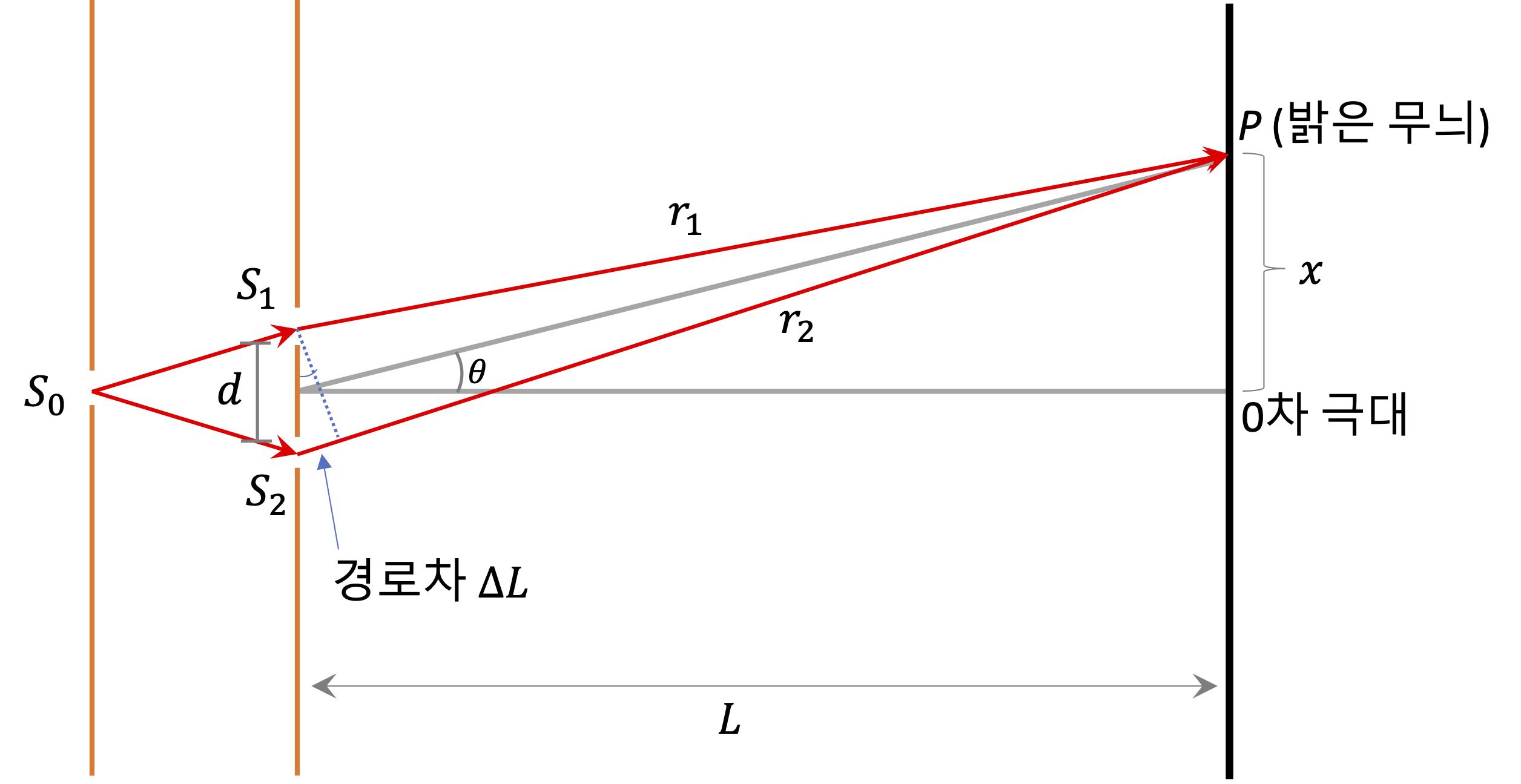
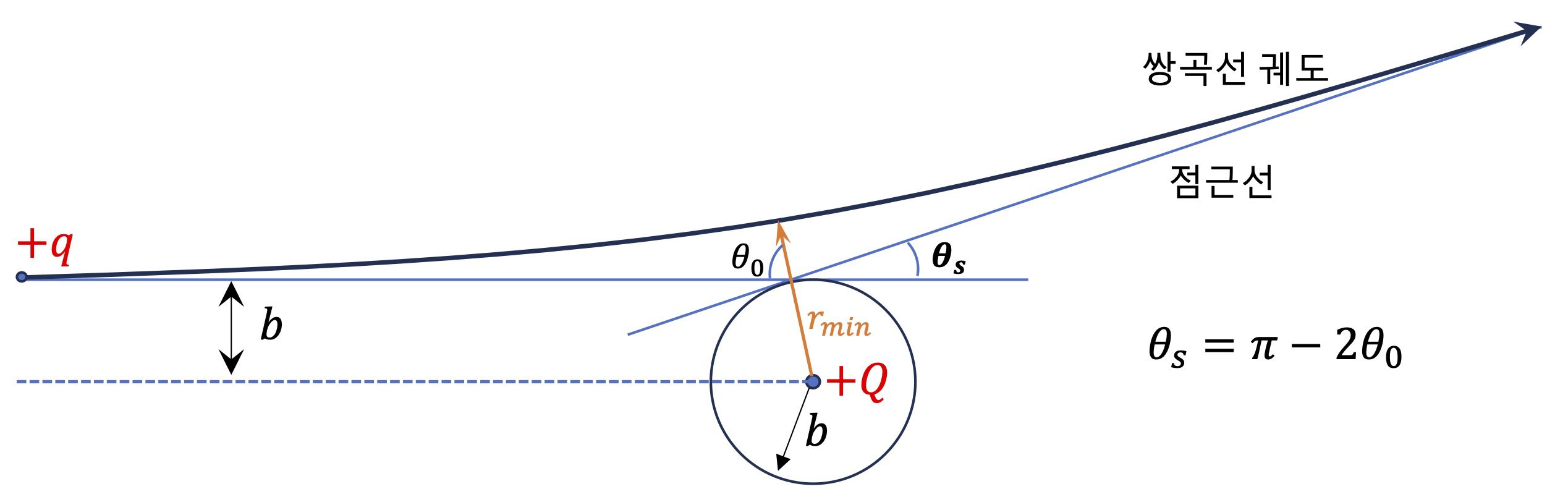
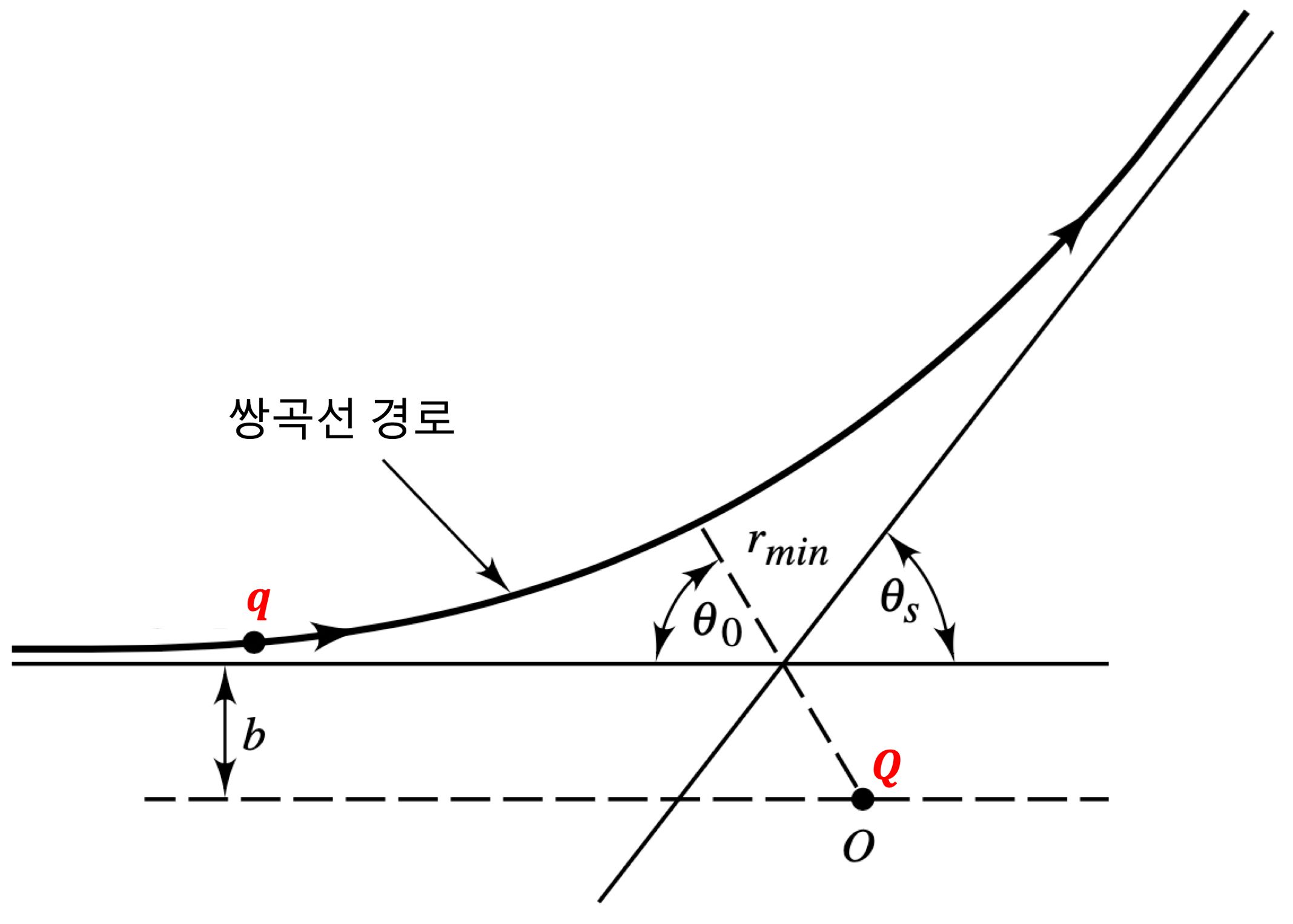
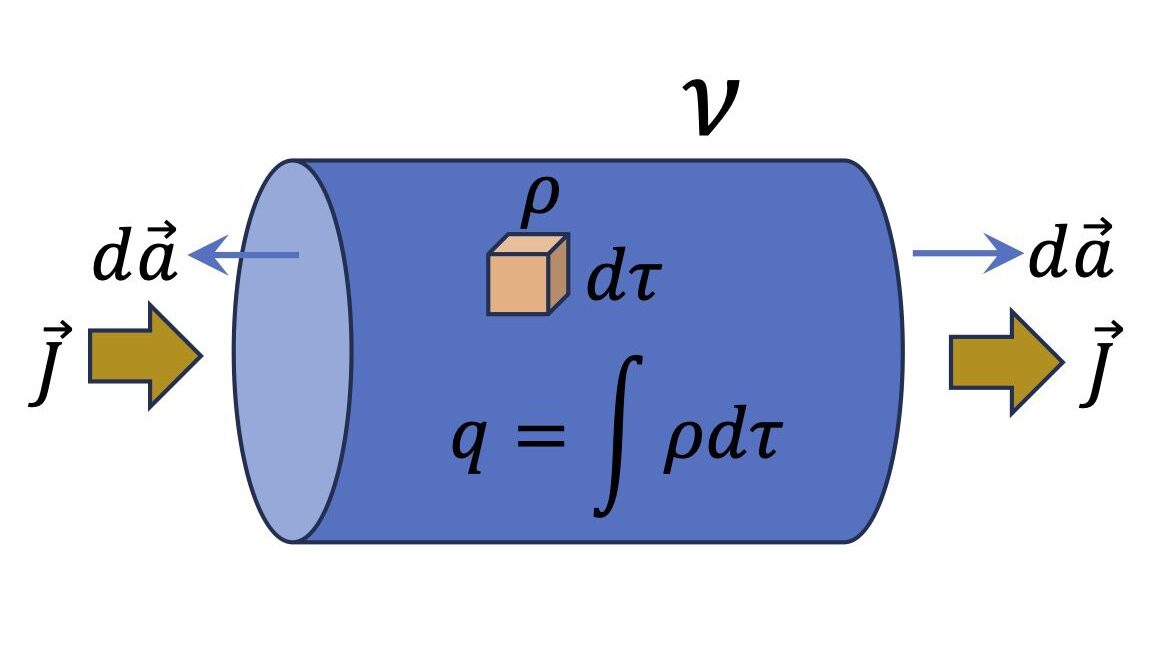
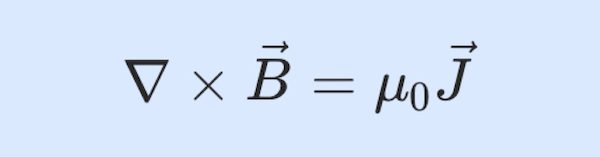간섭 무늬 : Young의 간섭 실험5 (1)
Young의 이중 슬릿 실험을 통해 간섭 무늬 생성 조건을 알아 봐요. 간섭 무늬 생성 원리를 이해하면 빛이 파동성을 갖는다는 성질을 이해할 수 있습니다. 고전적인 입장에서 빛이 만일 입자라면 서로 충돌하며 튕겨낼 뿐 서로 합쳐져 더 강해지거나 약해지는 것을 설명할 수 없기 때문이에요. 하지만 파동은 중첩(superposition) 현상을 통해 빛이 서로 만날 때 보강되거나 상쇄되는 현상을 만족스럽게 … Read more