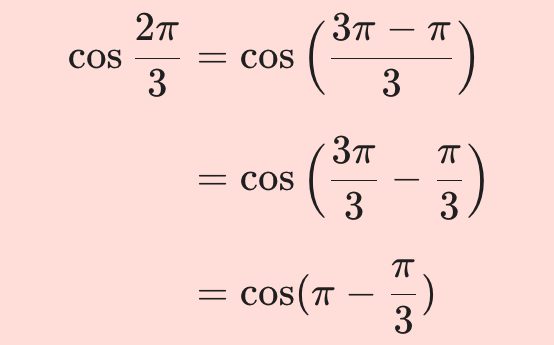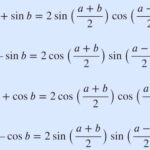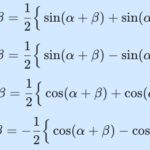cos 2pi/3 값 구하기

BallPen · 2024-01-21T11:43:23+09:00

cos 2pi/3 형식은 수학 공부를 하다보면 간혹 마주치는 문제 중 하나입니다. 이 문제의 값을 구하기 위해서는 특수각이 이용되는 삼각함수의 덧셈 형식이 되도록 식을 변형 한 후 삼각함수 합차 공식을 적용하여 구하면 됩니다.

Last Updated on 2024-01-21 by BallPen

cos 2pi/3, cos 4pi/3, sin 4pi/3 형식의 값을 구하는 방법입니다.

cos 2pi/3 형식은 삼각함수 공부를 하다보면 간혹 풀어야 하는 경우가 있어요. 이번 글에서는 이러한 형식으로 문제가 주어진 경우 그 값을 어떻게 구해야 하는지 설명드립니다.

우선 $\cos{{2 \pi}\over{3}}$ 를 아래의 방법으로 형태를 바꾸어 봐요.

\tag{1} \begin{align} \cos {{2 \pi}\over{3} } &= \cos\Big({{3\pi - \pi}\over3}\Big)\\[10pt] &= \cos\Big({{3\pi}\over{3}}-{\pi \over 3}\Big)\\[10pt] &=\cos(\pi - {{\pi}\over{3}}) \end{align}

그리고 삼각함수의 합차 공식을 적용합니다.

\tag{2} \begin{align} \cos (\pi - {{\pi}\over{3}}) &= \cos\pi\cos{{\pi}\over{3}} + \sin\pi\sin{{\pi}\over{3}}\\[10pt] &=-\cos{\pi \over 3}\\[10pt] &=-{1 \over 2} \end{align}

이 문제도 위의 문제와 동일한 방식으로 풀면 됩니다. 우선 식의 형태를 다음과 같이 바꿔보세요.

\tag{3} \begin{align} \cos {{4 \pi}\over{3} } &= \cos\Big({{3\pi + \pi}\over3}\Big)\\[10pt] &= \cos\Big({{3\pi}\over{3}}+{\pi \over 3}\Big)\\[10pt] &=\cos(\pi + {{\pi}\over{3}}) \end{align}

삼각함수의 합차 공식을 적용하세요.

\tag{4} \begin{align} \cos (\pi + {{\pi}\over{3}}) &= \cos\pi\cos{{\pi}\over{3}} - \sin\pi\sin{{\pi}\over{3}}\\[10pt] &=-\cos{\pi \over 3}\\[10pt] &=-{1 \over 2} \end{align}

유사 문제로써 이번에는 $\sin{{2 \pi}\over{3}}$ 를 풀어봐요. 푸는 요령은 위에서와 동일합니다.

먼저 식의 형태를 다음과 같이 바꿉니다.

\tag{5} \begin{align} \sin {{4 \pi}\over{3} } &= \sin\Big({{3\pi + \pi}\over3}\Big)\\[10pt] &= \sin\Big({{3\pi}\over{3}}+{\pi \over 3}\Big)\\[10pt] &=\sin(\pi + {{\pi}\over{3}}) \end{align}

이번에도 삼각함수 합차 공식을 적용하세요.

\tag{6} \begin{align} \sin (\pi + {{\pi}\over{3}}) &= \sin\pi\cos{{\pi}\over{3}} + \cos\pi\sin{{\pi}\over{3}}\\[10pt] &=-\sin{\pi \over 3}\\[10pt] &=-{\sqrt{3} \over 2} \end{align}

흥미롭고 도움이 되는 글이었나요? 리뷰를 부탁드립니다.

[Total: 1 Average: 5]