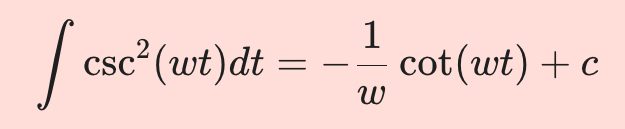(csc(wt))^2 적분

BallPen · 2024-02-16T00:35:11+09:00

(csc(wt))^2 적분 방법을 설명드립니다.

Last Updated on 2024-02-19 by BallPen

$\int \csc^2 (wt) dt$ 를 적분해 보겠습니다.

$(\csc(wt))^2$ 을 $t$ 에 대해 적분하면 다음과 같습니다. 여기서 $w$ 는 상수에요.

\tag{D1} \int \csc^2(wt)dt = - {1 \over w} \cot(wt)+c

위 (D1)식이 어떻게 유도되는지 함께 알아봐요.

우선 식을 다시 쓰면 다음과 같습니다.

\tag{1} \int \csc^2(wt)dt = \int {1 \over{\sin^2(wt)}}dt

(1)식의 우변에 ${{1}\over{\cos^2(wt)}}$ 을 분자와 분모에 곱합니다. 그러면 다음과 같아요.

\tag{2} \begin{align} \int \csc^2(wt)dt &= \int {1 \over{\sin^2(wt)}}dt\\[10pt] &=\int{{\color{blue}{1 \over{\cos^2(wt)}}} \over{\sin^2(wt)}{\color{blue}{{{\color{blue}{1}}} \over{\cos^2(wt)}}}}dt\\[10pt] &=\int{{\sec^2(wt)}\over{\tan^2(wt)}} dt \end{align}

그리고 (2)식의 분모에 있는 $\tan(wt)$ 를 $u$ 로 치환하겠습니다. 그리고 미분할게요.

\tag{3} \begin{align} &\color{blue}\tan(wt) = u\\[10pt] &w\sec^2(wt)dt = du\\[10pt] &\color{blue}\csc^2(wt)dt = {1 \over w} du \end{align}

(3)식의 첫번째와 마지막 줄을 (1)식에 대입하고 정리합니다.

\tag{4} \begin{align} \int \csc^2(wt)dt &= \int{1 \over u^2} {1 \over w} du\\[10pt] &={1 \over w} \int u^{-2} du\\[10pt] &={1 \over w} \Big( -u^{-1} +c\Big) \\[10pt] &=-{1 \over w} \Big({1 \over \tan(wt)}+c\Big)\\[10pt] &=-{1 \over w} \cot(wt) + c \end{align}

윗 식의 마지막 줄에서 $-{1 \over w}$ 과 적분상수 $c$ 의 곱을 상수 $c$ 로 나타내었어요. 어차피 상수와 상수의 곱은 다시 상수가 될 뿐입니다.

그 결과 (D1)식이 도출되었습니다.

흥미롭고 도움이 되는 글이었나요? 리뷰를 부탁드립니다.

[Total: 1 Average: 5]