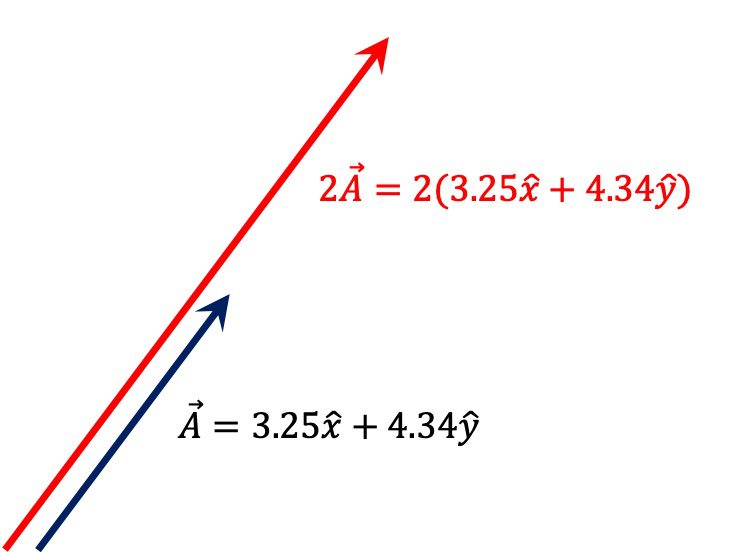
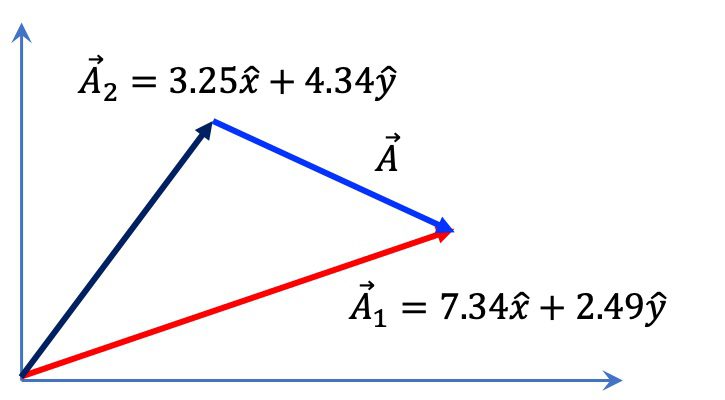
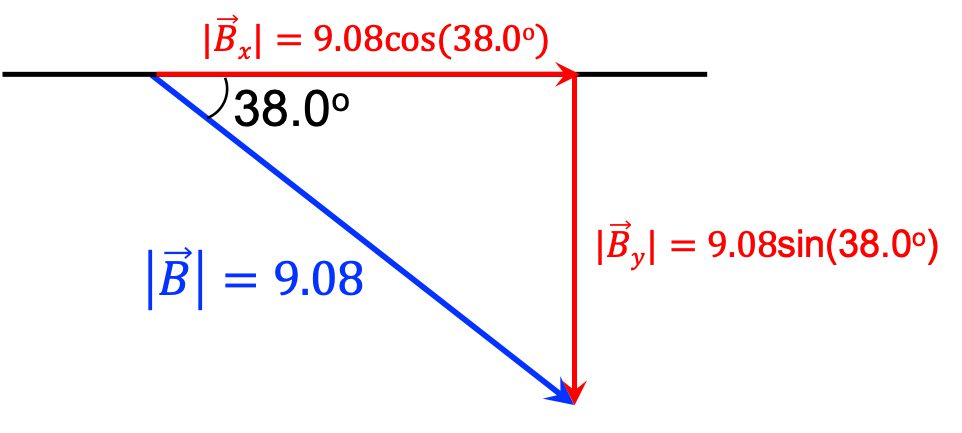
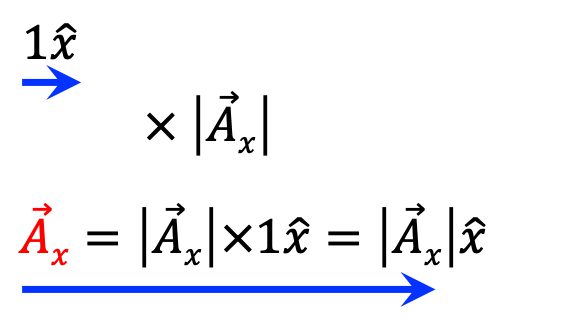벡터의 실수배 : 벡터에 스칼라를 곱하는 방법과 기하학적 의미3.7 (3)
벡터에 스칼라를 곱하여 벡터의 실수배를 연산하는 수학적 방법과 기하학적 의미를 소개합니다. 벡터의 실수배 연산에 대한 내용이 이번 글에서 다루어 집니다. 벡터와 관련된 다른 내용은 아래의 글들을 참고하시기 바랍니다. 순서대로 읽으면 벡터를 이해하는데 크게 도움을 받을 수 있어요. 아래는 이번 글의 목차입니다. Contents1. 벡터의 실수배 연산을 위한 수학적 방법1-1. 벡터와 스칼라의 차이1-2. 벡터의 양의 실수배1-3. 벡터의 … Read more