Last Updated on 2025-10-17 by BallPen
단위벡터 개념을 이해해야 벡터를 제대로 표기할 수 있습니다. 또한 벡터를 정규화하여 단위벡터를 만드는 방법을 설명드립니다.
단위벡터 (unit vector)는 크기가 1인 벡터를 말합니다. 과연 이러한 단위벡터는 왜 필요할까요? 또 벡터를 정규화한다고 하는데요. 정규화하는 방법과 공식을 알아보겠습니다.
우선 이전 글에서 다루었던 벡터의 작도, 벡터의 크기, 벡터의 성분에 대한 개괄적 내용이 궁금한 분은 여기를 누르세요.
이번 글의 목차입니다.
Contents
1. 단위벡터 의미
단위라고 하면 물리량을 표시할 때 크기를 나타내는 숫자 뒤에 어느 물리량인지를 알려주는 알파벳 기호가 우선 생각나실 것 같애요. 예를 들어 20 kg이라고 하면 kg이 단위이고 20은 질량의 크기라는 것을 알게 되죠.
그런데 단위벡터(unit vector)에서 단위는 그 계량 단위를 뜻하는 것이 아닙니다. 바로 상품의 한 개, 특정 임무를 하는 단체, 병원의 부서(과), 물질의 덩어리라는 측면에서의 단위로 보아야 합니다.
1-1. 단위길이와 단위질량
한가지 예를 들어 보겠습니다. 어느 물체의 길이가 10 m라고 해봐요. 그러면 10 m구나 하고 전체 길이를 하나로 생각하지 마시구요. 이렇게 생각해보세요.
10 m는 1 m의 길이가 10배되는 길이라고 생각해보세요. 이때 최소 덩어리가 되는 1 m를 단위길이라고 부르게 됩니다. 이것을 식으로 표현하면 아래와 같습니다.
\tag{1}
l = 10~\mathrm{m} = 10 \times1~\mathrm{m}이와 같은 방식으로 질량 3 kg은 단위질량 1 kg을 3배한 크기인 것이죠. 바로 아래 식과 같이 표현할 수 있습니다.
\tag{2}
m=3~\mathrm{kg} = 3 \times 1~\mathrm{kg}1-2. 단위벡터
이번에는 \vec{A} = 3 \hat{x} 라고 하는 벡터가 있다고 생각해 보세요. 이것도 위의 (1)과 (2)식처럼 생각하면 1\hat{x}을 3배한 크기가 \vec{A}가 되는 것으로 생각할 수 있습니다. 아래 식처럼요.
\tag{3}
\vec{A} = 3 \hat{x} = 3 \times 1\hat{x}이때 숫자 3은 지난 글에서 설명한 것처럼 벡터 \vec{A}의 방향이 없는 크기이고, 1\hat{x}는 크기가 1이고 x방향을 향하는 벡터, 즉 단위벡터를 나타냅니다.
결국 단위벡터를 알면 크기 만큼의 배수를 해줌으로써 벡터를 표기할 수 있게 되는 것이죠.
참고로 단위벡터 표기는 \hat{x}, ~\hat{y}, ~\hat{z} 또는 i, ~j, ~k의 단위벡터 기호를 사용하여 표기하는 것이 일반적입니다.
2. 단위벡터의 기하학적 의미
(3)식에서와 같이 벡터는 단위벡터를 어느 크기만큼 배수를 한 것으로 볼 수 있습니다.
그렇다면 x방향을 향하는 벡터, y방향을 향하는 벡터, 비스듬한 방향을 향하는 벡터에서 단위벡터는 기하학적으로 어떤 의미를 갖는지 각각 살펴보겠습니다.
2-1. 좌표축에 평행한 벡터의 단위벡터
아래 그림 상단에는 x방향으로 크기가 1인 단위벡터 1\hat{x}의 화살표가 그려져 있습니다. 이 단위벡터에 방향이 없는 크기를 곱하면 벡터가 된다고 말씀드렸는데요.
아래 그림에서 크기를 벡터 \vec{A_x}에 절대값 기호를 취한 |\vec{A_x}|로 나타내었습니다. 이것은 벡터 \vec{A_x}의 크기를 상징하는 기호로 보시면 됩니다.
그래서 단위벡터 1\hat{x}에 벡터의 크기 |\vec{A_x}|를 곱하여 얻어진 결과는 \vec{A_x} = |\vec{A_x}|\hat{x}로 쓸 수 있습니다.
\tag{4}
\begin{aligned}
\vec{A_x} &= 크기\times단위벡터\\[10pt]
&=|\vec{A_x}|~\hat{x}
\end{aligned}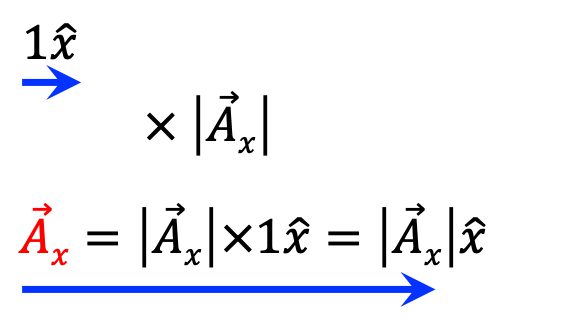
기하학적으로 벡터 \vec{A_x}의 화살표는 위 그림과 같이 단위벡터의 화살표 방향을 x방향으로 그대로 유지하면서 벡터의 크기 |\vec{A_x}|만큼 화살표의 길이를 배수 한 것으로 보시면 됩니다.
이와는 반대로 만일 \vec{A_x}가 주어질 때 단위벡터는 어떻게 구할 수 있을까요? 바로 (4)식의 양변을 |\vec{A_x}|로 나누어주면 됩니다. 아래 (5)식 처럼요.
\tag{5}
\hat{x} = {{\vec{A_x}}\over{|\vec{A_x}|}}기하학적으로는 \vec{A_x}의 방향은 그대로 유지하되 화살표의 길이를 크기 값 |\vec{A_x}|로 나누는 것으로 이해하시면 됩니다.
– 연습문제 1번, 2번
(문제1) 단위벡터가 x 방향을 향한다고 했을 때 크기가 15인 벡터 \vec{A_x}를 표기하여라.
(solution)
벡터는 단위벡터에 벡터의 크기를 곱하면 되므로 아래와 같이 표기한다.
\tag{6}
\begin{aligned}
\vec{A_x} &= |\vec{A_x}|\hat{x}\\[10pt]
&=15\hat{x}
\end{aligned}(문제2) 어느 벡터가 \vec{v_x} = 8~\hat{x}로 주어졌을 때 이 벡터의 단위벡터를 구하여라.
(solution)
벡터의 단위벡터를 구하기 위해서는 (5)식을 적용한다. 즉 벡터를 벡터의 크기로 나누면 된다.
\tag{7}
\begin{aligned}
\hat{x} &= {{\vec{v_x}}\over{|\vec{v_x}|}} \\[10pt]
&= {{8~\hat{x}}\over{8}}\\[10pt]
&=1\hat{x}
\end{aligned}이번에는 아래 그림처럼 y축 방향을 향하는 단위벡터 1\hat{y}가 왼쪽 하단에 화살표로 그려져 있습니다.
이 단위벡터에 벡터의 크기 |\vec{A_y}|를 곱하면 벡터 \vec{A_y}가 얻어집니다. 방향만 y축으로 달라졌을 뿐 (4)식과 동일한 개념입니다.
\tag{8}
\begin{aligned}
\vec{A_y} &= 크기\times단위벡터\\[10pt]
&=|\vec{A_y}|~\hat{y}
\end{aligned}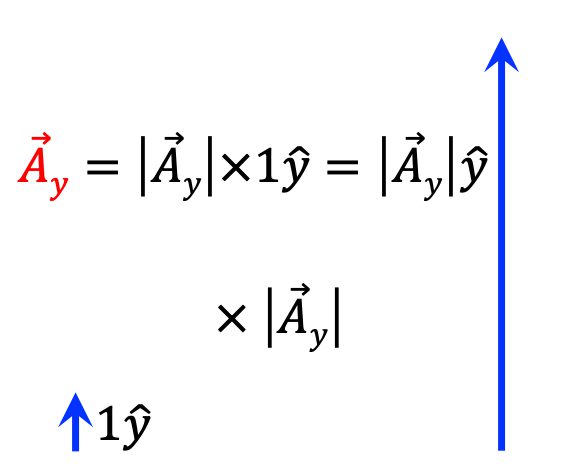
기하학적으로 \vec{A_y}는 위 그림과 같이 단위벡터 1\hat{y}에서 화살표의 방향은 그대로 유지하되 길이만 |\vec{A_y}|배로 화살표가 길어진 것입니다.
이와는 반대로 만일 \vec{A_y}가 주어질 때 단위벡터는 어떻게 구할 수 있을까요? 바로 (8)식의 양변을 |\vec{A_y}|로 나누어주면 됩니다. 아래 (9)식 처럼요.
\tag{9}
\hat{y} = {{\vec{A_y}}\over{|\vec{A_y}|}}기하학적으로 \vec{A_y}의 화살표 방향은 그대로 유지하되 화살표 길이를 크기 값 |\vec{A_y}|로 나누는 것으로 이해하시면 됩니다.
– 연습문제 3번, 4번
(문제3) 단위벡터가 y 방향을 향한다고 했을 때 크기가 15\sqrt{3}인 벡터 \vec{A_y}를 표기하여라.
(solution)
벡터는 단위벡터에 벡터의 크기를 곱하여 구한다. 그러므로 아래와 같이 표기한다.
\tag{10}
\begin{aligned}
\vec{A_y} &= |\vec{A_y}|~\hat{y}\\[10pt]
&=15\sqrt{3}\hat{y}
\end{aligned}(문제4) 어느 벡터가 \vec{v_y} = 10~\hat{y}로 주어졌을 때 이 벡터의 단위벡터를 구하여라.
(solution)
벡터의 단위벡터를 구하기 위해서는 (9)식을 적용하면 된다. 즉 벡터를 벡터의 크기로 나누어 준다.
\tag{11}
\begin{aligned}
\hat{y} &= {{\vec{v_y}}\over{|\vec{v_y}|}} \\[10pt]
&= {{10~\hat{y}}\over{10}}\\[10pt]
&=1\hat{y}
\end{aligned}2-2. 비스듬한 벡터의 단위벡터
이전 글에서 비스듬한 벡터는 x성분 벡터와 y성분 벡터로 분해할 수 있고, 각성분의 합으로 벡터를 표기한다고 설명드렸습니다. 이를 식으로 표현하면 아래와 같습니다.
\tag{12}
\begin{aligned}
\vec{A} &= x성분 벡터+y성분 벡터\\[10pt]
&=\vec{A_x} + \vec{A_y}\\[10pt]
&= |A_x|\hat{x} + |A_y|\hat{y}
\end{aligned}또한 벡터는 단위벡터를 이용해서도 표현할 수 있습니다. 아래 (13)식과 같이요. 다만 x와 y축에 평행하지 않고 비스듬하게 주어져 있는 벡터의 단위벡터를 어떻게 구하는지 아직 모르므로 그냥 ‘단위벡터’라고 표기하겠습니다.
\tag{13}
\begin{aligned}
\vec{A} &= 벡터의 크기\times단위벡터\\[10pt]
&=|\vec{A}|\times 단위벡터
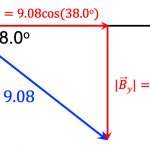
\end{aligned}기하학적으로는 아래 그림과 같이 이해할 수 있습니다. 그림에 가로축으로 부터 55.0^\circ 방향으로 그려진 파랑색 벡터 \vec{A}가 있습니다.
벡터 \vec{A}인 파랑색 벡터는 갈색으로 주어진 x성분의 벡터 \vec{A_x}와 y성분의 벡터 \vec{A_y}로 분해되어 표기될 수 있습니다.
또한 \vec{A}의 단위벡터를 알고 있다면 이 단위벡터를 |\vec{A}|배하여 벡터를 표현할 수도 있습니다.
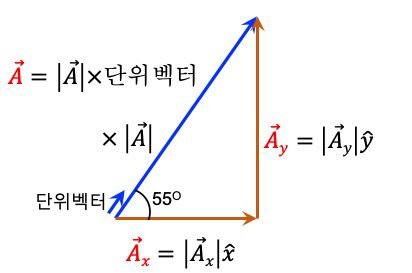
문제는 비스듬한 벡터의 단위벡터를 어떻게 구하느냐 인데요. 이를 구하기 위해서는 벡터 정규화를 알아야 합니다. 이에 대해서는 아래에서 별도로 다루겠습니다.
일단 (12)식을 적용하는 연습문제 하나만 풀어보고 계속 이어가겠습니다.
– 연습문제 5번
(문제5) 위 그림과 같이 가속도 벡터 \vec{A}가 55.0^\circ 위쪽 방향을 향하고 있다. 이 벡터의 크기는 8.70 m/s2이다. 이 벡터를 (12)식과 같은 형태로 표기하여라.
(solution)
(12)식의 형태로 벡터를 표기하기 위해서는 x와 y성분의 벡터 크기를 아래와 같이 각각 구해야 합니다.
\tag{14}
\begin{aligned}
|\vec{A_x}| &= 8.70\cos(55.0^\circ)\\[10pt]
&=4.99 ~\mathrm{m/s^2}\\[10pt]
|\vec{A_y}| &= 8.70 \sin(55^\circ)\\[10pt]
&=7.13~\mathrm{m/s^2}
\end{aligned}결국 가속도 벡터 \vec{A}는 아래와 같이 표현할 수 있습니다.
\tag{15}
\begin{aligned}
\vec{A} &= |A_x|\hat{x} + |A_y|\hat{y}\\[10pt]
&=(4.99\hat{x} + 7.13\hat{y})~\mathrm{m/s^2}
\end{aligned}3. 벡터 정규화로 구하는 단위벡터
벡터 정규화(vector normalize)를 한다는 것은 벡터의 단위벡터를 구한다는 말입니다. 그렇다면 주어진 벡터에서 단위벡터를 어떻게 구할 수 있을까요? 이미 앞에서 x과 y에 평행한 벡터의 단위벡터를 구하는 방법을 설명 드렸습니다.
바로 (5)식과 (9)식이 그것이죠. 벡터를 그 벡터의 크기로 나누면 크기가 1이고 방향을 가진 단위벡터가 구해지는데요. 이 과정을 정규화한다고 말하는 것입니다.
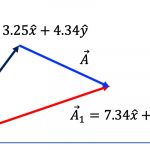
그렇다면 아래 그림처럼 비스듬한 벡터의 단위벡터를 어떻게 구할 수 있을까요? 이 단위벡터도 크기가 1이고 방향은 아래 그림에서와 같이 \vec{A}와 동일한 방향을 가져야 합니다. 구하는 방법은 벡터를 크기로 나누는 방법을 그대로 사용합니다.
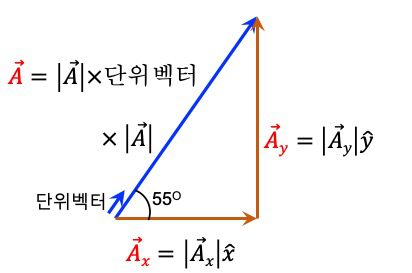
예를 들어 (12)식과 (13)식은 모두 벡터 \vec{A}를 나타내는 표현식입니다. 그러므로 두 표현식을 활용하여 단위벡터를 구하면 다음과 같은 벡터 정규화 공식을 얻을 수 있습니다.
\tag{16}
\begin{aligned}
|\vec{A}|\times 단위벡터 &=\vec{A} = |A_x|\hat{x} + |A_y|\hat{y}\\[10pt]
단위벡터 &= {{\vec{A}}\over{|\vec{A}|}}\\[10pt]
&={{|A_x|\hat{x} + |A_y|\hat{y}}\over{|\vec{A}|}}
\end{aligned}– 연습문제 6번
(문제6) 위 그림에 대한 벡터는 (15)식과 같이 주어진다고 가정하자. (a) 이 벡터의 크기를 구하여라. (b)벡터 정규화를 통해 벡터의 단위벡터를 구하여라. (c) 단위벡터를 활용하여 벡터를 (13)식의 형태로 표기하여라. (d) 단위벡터의 크기가 1이 되는지를 보여라.
(solution)
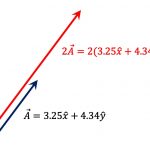
(a) 문제에서 주어진 벡터는 다음과 같다.
\tag{17}
\begin{align}
\vec{A} &=4.99\hat{x} + 7.13\hat{y}
\end{align}벡터의 크기는 피타고라스 정리(Pythagorean theorem)를 활용한다. (17)식에서 x방향의 크기가 4.99이고, y방향의 크기가 7.13이므로 빗변의 길이에 해당하는 벡터의 크기는 다음과 같이 8.70이 나온다.
\tag{18}
\begin{aligned}
|\vec{A}| &= \sqrt{4.99^2 + 7.13^2}\\[10pt]
&=8.70
\end{aligned}(b) 벡터 정규화는 (16)식과 같이 벡터를 벡터의 크기로 나눔으로써 단위벡터를 구하는 절차를 말한다. 그러므로 다음과 같이 단위벡터를 구할 수 있다.
\tag{19}
\begin{aligned}
단위벡터 &= {{\vec{A}}\over{|\vec{A}|}}\\[10pt]
&={{|A_x|\hat{x} + |A_y|\hat{y}}\over{|\vec{A}|}}\\[10pt]
&={{4.99\hat{x}+7.13\hat{y}}\over{8.70}}\\[10pt]
&=0.574\hat{x} + 0.820\hat{y}
\end{aligned}(c) 벡터 표기를 (13)식과 같이 표현하면 다음과 같다.
\tag{20}
\begin{aligned}
\vec{A} &= 벡터의 크기\times단위벡터\\[10pt]
&=|\vec{A}|\times 단위벡터\\[10pt]
&=8.70\times (0.574\hat{x} + 0.820\hat{y})\\[10pt]
&=8.70(0.574\hat{x} + 0.820\hat{y})\\
\end{aligned}(d) (19)식에서 구한 단위벡터의 크기가 정말 1이 나오는지를 확인하기 위해서는 다음과 같이 피타고라스 정리를 활용한다.
\tag{21}
\begin{aligned}
|단위벡터| &= \sqrt{0.574^2 + 0.820^2}\\[10pt]
&= 1.00
\end{aligned}벡터 정규화를 통해 구한 단위벡터의 크기가 1이 나왔다.
4. 단위벡터와 벡터 정규화 요약
- 단위벡터는 크기가 1이고 방향을 갖는 벡터를 말한다.
- 벡터란 단위벡터를 벡터의 크기만큼 배수한 것으로 볼 수 있다.
- 단위벡터는 벡터를 벡터의 크기로 나누는 벡터 정규화 공식을 통해 구할 수 있다.
5. 벡터 관련 추천 글
- 벡터, 벡터의 작도, 벡터의 크기, 벡터의 성분
- 단위벡터 의미와 벡터 정규화
- 벡터의 방향 표기를 정확하게 하는 방법
- 벡터의 덧셈 : 기하학적 표현과 수학적 처리
- 벡터의 뺄셈 : 벡터의 변화량을 구하는 도구



정성들인 문서네요. 내용도 훌륭하고요. 질문을 막 시작한 저에게는 아주 많은 도움이 되고 있습니다. 그리고 준비하는 것에도 많은 도움이 되고 있습니다. 감사합니다
방문해 주셔서 감사합니다. ^^