Last Updated on 2025-09-26 by BallPen
전기용량 리액턴스와 유도 리액턴스를 구하는 예제입니다.
리액턴스 예제 풀이입니다. 아래는 이번 글의 목차에요.
이 글에 사용된 그림 파일 원본은 아래에서 다운 받으세요. 키노트 파일이 원본이고 파워포인트 파일은 키노트 파일을 변환한거라 일부 호환성 문제가 있을 수 있어요. 편집해서 사용하시기 바랍니다.
맥 키노트 파일: reactance_examples.key
파워포인트 파일: reactance_examples.pptx
1. 전기용량 리액턴스 예제
[문제]
전기용량 8.00~\rm \mu F인 축전기가 실효 전압이 150 V이고 진동수가 60 Hz인 교류발전기 단자에 연결되었다. 전기용량 리액턴스와 회로를 통과하는 실효 전류를 각각 구하여라.
[풀이]
문제 상황을 그림으로 나타내면 다음과 같아요.
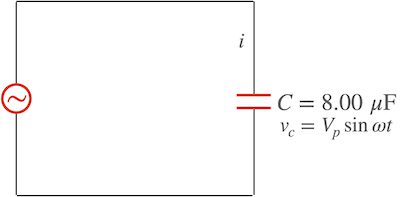
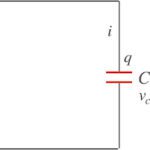
![[그림 1] 축전기가 교류전원과 연결되면 전기용량 리액턴스가 발생합니다.](https://ballpen.blog/wp-content/uploads/2024/06/example1-1024x505.jpg)
그림과 같이 축전기가 교류전원과 연결되어 있는데요. 회로에 축전기 하나 뿐이므로 축전기 양단의 전압 v_c는 교류전원 전압과 같아요.
전기용량 리액턴스 X_c는 공식을 활용해 구하면 다음과 같아요.
\tag{1-1}
\begin{aligned}
X_c = {1 \over {\omega C}} &= {1 \over {2 \pi fC}}\\[10pt]
&={1 \over {2 \pi \times 60~\rm Hz \times (8.00 \times 10^{-6}~\rm F})}\\[10pt]
&=3.32 \times10^2 ~\rm \Omega\\[10pt]
&=332 ~\rm \Omega
\end{aligned}즉, [그림 1] 회로의 전기용량 리액턴스는 332~\rm \Omega이에요.
자, 이번에는 회로를 통과하는 전류를 구해야 하는데요.
축전기에 걸린 실효 전압 V_{rms}이 문제에 주어져 있고, 리액턴스 X_c도 구했으므로 회로를 통과하는 실효전류 I_{rms}는 옴의 법칙을 적용하면 구할 수 있어요.
\tag{1-2}
\begin{aligned}
I_{rms} &= {{V_{rms}}\over{X_c}}\\[10pt]
&={{150~\rm V}\over{332 ~\Omega}}\\[10pt]
&=0.452~\rm A
\end{aligned}2. 유도 리액턴스 예제
[문제]
L = 2~\rm mH인 인덕터에 f=60~\rm kHz의 전원신호가 연결되었다. 유도 리액턴스를 구하여라. 그리고 인덕터에 실효치 전류 0.50~\rm mA가 흐를 때 인덕터 양단의 실효치 전압은 얼마가 되겠는가?
[풀이]
문제 상황을 그림으로 나타내면 다음과 같아요.
![[그림 2] 인덕터가 교류전원과 연결되면 유도 리액턴스가 발생합니다.](https://ballpen.blog/wp-content/uploads/2024/06/example2-1-1024x489.jpg)
여기서도 회로에 인덕터 하나 뿐이므로 인덕터 양단의 전압 v_L은 교류 전원전압과 같아요.
유리 리액턴스 X_L은 공식을 활용해 다음과 같이 구할 수 있어요.
\tag{2-1}
\begin{aligned}
X_L = \omega L &= 2 \pi f L \\[10pt]
&=2\pi \times (60 \times10^{3}~\rm Hz)\times(2\times10^{-3}~\rm H)\\[10pt]
&=754~\Omega
\end{aligned}즉, [그림 2] 회로의 유도 리액턴스는 754~\rm \Omega입니다.
회로를 통과하는 전류는 옴의 법칙을 적용하면 구할 수 있는데요. 문제에서 회로를 통과하는 실효치 전류 I_{rms}가 주어져 있으므로 인덕터 양단의 실효치 전압 V_{rms}는 다음과 같습니다.
\tag{2-2}
\begin{aligned}
V_{rms} &= I_{rms} X_L\\[10pt]
&=(0.50\times 10^{-3}~\rm A)(754~\Omega)\\[10pt]
&=0.38~\rm V
\end{aligned}