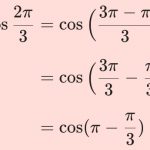코사인 법칙(law of cosines)

Last Updated on 2024-01-06 by BallPen

코사인 법칙을 유도해 보겠습니다.

코사인 법칙(law of cosines)이란 삼각형 두 변의 길이와 그 사이각을 알고 있을 때 나머지 한 변의 길이를 구할 수 있는 법칙을 말해요.

그런데 이 수식에 삼각함수의 cosine이 들어가 있어 코사인 법칙이라고 부릅니다.

코사인 법칙에 따르면 삼각형의 세변 길이를 a,~b, ~c라 하고 변 a의 맞은 편에 있는 각을 \alpha, 변 b의 맞은 편에 있는 각을 \beta, 변 c의 맞은 편에 있는 각을 \gamma라고 할 때 다음의 관계가 성립합니다.

\tag{D1}
\begin{align}
&a^2 = b^2 + c^2 - 2bc \cos\alpha\\
&b^2 = c^2 + a^2 - 2ca \cos\beta\\
&c^2 = a^2 + b^2 - 2ab \cos \gamma
\end{align}

그럼 이제부터 위 (D1)식이 어떻게 유도되는지 알아볼께요.

아래는 이번 글의 목차입니다.

1. 코사인 법칙 증명

코사인 법칙은 기하학적 해석과 벡터적 해석을 거쳐 증명될 수 있어요. 두 방법의 결과는 모두 동일해요. 하나씩 설명드릴게요.

1-1. 기하학적 해석

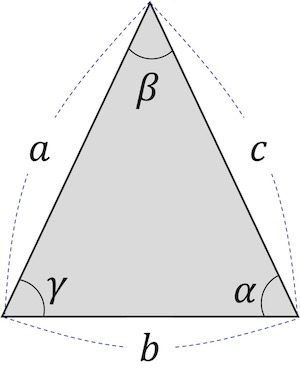
아래 [그림 1]에 삼각형이 하나 있는데요.

삼각형 각 변의 길이가 a, b, c이고 각 변에 대응하는 각도가 \alpha, \beta, \gamma입니다.

이때 [그림 2]의 빨강색 세로선과 같이 삼각형을 이등분하면 좌우로 직각삼각형이 만들어지는 것을 볼 수 있어요.

이때 각 \beta는 그림을 단순화하기 위해 그리지 않았어요.

[그림 2]에서 중앙의 빨강색 세로선을 기준으로 왼쪽에 있는 직각삼각형을 보세요.

그러면 그림에 표기한 것처럼 빨강색 세로선의 길이, 즉 직각삼각형의 높이는 a \sin \gamma가 되고, 밑변의 길이는 a \cos \gamma가 됩니다.

그러면 이번에는 오른쪽 직각삼각형의 빗변 c의 길이를 제곱한 c^2을 구한다고 한다면 어떻게 하면 될까요?

네 맞아요. 피타고라스 정리를 이용하면 되는데요. 직각삼각형의 높이와 밑변을 각각 제곱한 후 서로 합하면 빗변 길이의 제곱과 같아지게 되므로 다음과 같이 표현될 수 있어요.

\tag{1}
\begin{align}
c^2 = (a \sin \gamma)^2 + (b-a \cos \gamma)^2
\end{align}

자 그러면 (1)식을 더 정리해 보겠습니다.

\tag{2}
\begin{align}
c^2 &= (a^2 \sin^2 \gamma) + (b^2 - 2ab \cos \gamma +a^2 \cos^2 \gamma)\\
&=a^2(\sin^2 \gamma + \cos^2 \gamma) + b^2-2ab \cos \gamma\\
&=a^2 + b^2 - 2ab\cos \gamma\\
\end{align}

(2)식의 가장 마지막 줄은 코사인 법칙인 (D1)의 세번째 식과 동일합니다. 이와 같은 방식으로 a^2과 b^2도 구하면 코사인 법칙을 모두 유도할 수 있어요.

\tag{3}
\begin{align}
&a^2 = b^2 + c^2 - 2bc \cos\alpha\\
&b^2 = c^2 + a^2 - 2ca \cos\beta\\
&c^2 = a^2 + b^2 - 2ab \cos \gamma
\end{align}

1-2. 벡터적 해석

그러면 이번에는 벡터적 해석을 통해 코사인 법칙을 유도해 보겠습니다.

아래 [그림 3]은 [그림 1]과 그 형태가 같습니다만, 삼각형의 각 변이 벡터 화살표로 주어져 있어요. 또한 그림을 단순히 하고자 내각 \alpha와 \beta는 그림에 표기하지 않았습니다.

[그림 3]의 각 벡터는 벡터의 덧셈 규칙에 따라 다음 (4)식처럼 표현될 수 있습니다.

\tag{4}
\begin{align}
\vec c = \vec a + \vec b
\end{align}

그러면 이번에는 (4)식의 양변을 벡터 \vec c로 스칼라곱을 취해보겠습니다. 그러면 다음과 같습니다.

\tag{5}
\begin{align}
\vec c \cdot \vec c =c^2&= (\vec a + \vec b) \cdot \vec c\\
&=(\vec a + \vec b) \cdot (\vec a + \vec b)\\
&=\vec a \cdot \vec a + \vec a \cdot \vec b + \vec b \cdot \vec a + \vec b \cdot \vec b\\
&=a^2 + b^2 + 2 \color{blue}\vec a \cdot \vec b\\
\end{align}

(5)식의 가장 마지막 줄에 \vec a \cdot \vec b가 있어요.

이 스칼라곱의 크기를 구하기 위해서는 벡터 \vec a와 벡터 \vec b 사이의 각도가 필요한데요. 자칫 잘 못 생각하면 [그림 3]에서 \gamma로 착각할 수 있는데 그렇지 않아요.

벡터의 사이각을 구하기 위해서는 두 벡터의 꼬리를 서로 접촉시켰을 때의 각도를 말합니다. 그러므로 벡터 \vec a를 평행이동하여 벡터 \vec b의 꼬리와 접촉되게 만들면 아래 [그림 4]와 같아집니다.

바로 [그림 4]에서 \theta가 두 벡터의 사이각이 되는 거에요. 그리고 \theta는 \pi - \gamma와 같다는 것도 알 수 있습니다. 이러한 관계를 이용해 (5)식의 가장 마지막 줄을 다시 쓰면 아래와 같습니다.

\tag{6}
\begin{align}
c^2 &= a^2 + b^2 + 2\vec a \cdot \vec b\\
&=a^2 + b^2 + 2ab\cos \theta\\
&=a^2 + b^2 + 2ab \cos(\pi - \gamma)\\
&=a^2 + b^2 + 2ab(\cos \pi \cos \gamma + \sin \pi \sin \gamma)\\
&=a^2 + b^2 - 2ab \cos \gamma
\end{align}

결국 (6)식의 가장 마지막 줄은 (D1)식으로 주어진 코사인 법칙의 세번째 식과 동일함을 알 수 있어요.

이러한 방식으로 a^2과 b^2을 구하면 다음의 모든 관계를 구할 수 있습니다.

\tag{7}
\begin{align}
&a^2 = b^2 + c^2 - 2bc \cos\alpha\\
&b^2 = c^2 + a^2 - 2ca \cos\beta\\
&c^2 = a^2 + b^2 - 2ab \cos \gamma
\end{align}

3. 코사인 법칙 연습문제

(문제) 한변 a의 길이가 4.0 cm이고, 다른 한 변 b의 길이가 3.0 cm인 삼각형이 있다. 그리고 그 두 변이 끼고 있는 각도 \theta가 25^{\circ}라고 할 때 다른 한 변 c의 길이를 구하여라.

(풀이) 삼각형의 두변의 길이가 주어졌고, 그 두 변 사이의 각도가 주어져 있으므로 코사인 법칙을 적용합니다.

\tag{E1}
\begin{align}
c &= \sqrt{a^2 + b^2 - 2ab \cos \theta}\\
&=\sqrt{(4.0~ \mathrm{cm})^2 + (3.0~\mathrm{cm})^2 - 2(4.0~\mathrm{cm})(3.0~\mathrm{cm})\cos(25^{\circ})}\\
&\approx 1.8~\mathrm{cm}
\end{align}

다른 한 변의 길이는 1.8 cm 입니다.

Related posts.

청소년 가출 이유, 가장 큰 이유는 학업부담이 2위, 그렇다면 1위는? 다문화 신혼부부 출신 국적. 미국 남편, 중국 아내가 2위, 그럼 1위는? 강력범죄 피해자는 무엇을 하고 있었을까? 2위는 취침중, 그럼 1위는? 연금 월평균 수령액. 10년전 35만원, 그럼 지금은? 미세먼지 농도. 답답해! 해마다 줄어가는 건가, 늘어가는 건가? 청소년 알레르기 비염 – 청소년 10명중 3명 이상이 진단 받아 창업 기업 수에 대한 업종별 최근 통계를 확인해 보세요 미분방정식 예제1 : -ydx + xdy =0