등적 과정 (isochoric process)

Last Updated on 2022-07-03 by BallPen

열역학적 과정 중 등적 과정에 대한 이야기 입니다.

등적 과정(isochoric process) 또는 정적 과정은 대표적 열역학적 과정 중의 하나입니다. 열역학적 과정에는 등적 과정 뿐만 아니라 등온 과정, 단열 과정, 등압 과정 등이 있습니다.

이번 글에서는 기체의 분자 운동을 고려하여 등적 과정을 알아 봐요.

함께 시작해보겠습니다.

아래는 이번 글의 목차입니다.

1. 열역학 제1법칙

어떤 용기에 들어있는 기체 분자의 운동을 통해 등적 과정을 정확히 이해하기 위해서는 우선 열역학 제1법칙을 알아야 합니다. 아래에 몇개의 수식이 나오는데요. 거시적인 관계만 알면 되니, 구체적인 수식이 어떻게 유도되는가를 너무 고민하지 마세요.

열역학은 용기로 전달되는 열량(heat)과 기체분자가 한 일(work)사이의 관계를 설명하는 학문입니다. 사실 열량과 일이 서로 다른 개념인 것처럼 보이지만 두 개념의 단위는 에너지 단위 J로서 서로 같습니다. 결국 두 개념은 형태만 다를 뿐 모두 에너지인 것이죠.

이때 열량 Q와 일 W사이에는 다음 (1)식의 관계가 성립합니다. 그리고 이 관계를 열역학 제1법칙이라고 하죠.

\tag{1}
\Delta U = Q-W

1-1. 내부에너지

(1)식에서 \Delta U는 내부에너지라고 불리는 양의 변화량입니다. 내부에너지는 기체 분자들의 운동에너지와 분자들 간의 위치에너지 등 분자 자체에 저장되는 모든 에너지를 말합니다. 단원자 기체를 가정하면 내부에너지 U는 아래 (2)식과 같이 온도 T에 비례합니다.

\tag{2}
U= {3 \over 2}nRT

여기서 n은 기체의 몰수이며, R은 기체상수입니다. 또한 (2)식의 온도 T는 아래 (3)식과 같이 기체 분자의 전체 평균 운동에너지에 비례합니다.

\tag{3}
KE = N \Big( {1 \over 2} m \bar{v^2} \Big) ={3 \over 2} N k_B T

(3)식에서 N은 용기내에 있는 기체분자의 총 수, k_B는 볼츠만상수를 뜻합니다.

결국 (2)식과 (3)식을 종합하면 내부에너지 \Delta U는 다음의 관계가 성립합니다.

\tag{4}
\Delta U \propto \Delta T \propto\Delta{KE}

정리하면 어느 용기에 들어있는 기체의 내부에너지 변화량이라는 것은 기체분자의 온도 변화에 비례합니다. 또한 기체분자의 온도 변화는 분자의 운동에너지 변화량에 비례하는 것이죠.

바꾸어 말하면 기체분자의 운동에너지가 증가하면 분자의 온도가 상승한 것이고 이것은 곧 내부에너지가 증가한 것으로 간주하면 됩니다.

한번 더 강조하면 기체분자의 운동에너지, 즉 기체분자의 속력이 빨라지면 온도가 상승한 것이고 기체의 내부에너지가 증가한 것으로 보면 되요.

1-2. 열량

이번에는 (1)식의 열량 Q에 관한 이야기 입니다.

열량이란 온도차이에 의해 계로 전달되거나 나오는 에너지입니다. 여기서 중요한 것은 온도차이가 있어야 열량의 교환이 일어납니다. 이때 뜨거운 곳에서 차가운 곳으로 열량이 전달되죠.

[그림 1] 가스레인지의 뜨거운 불꽃으로부터 차가운 냄비로 열량이 전달됩니다.(사진은 Pixabay로부터 입수된 Steve Buissinne님의 이미지 입니다.)

[그림 1]을 보면 가스레인지 불꽃이 냄비를 가열하고 있어요. 그러면 뜨거운 불꽃에서 차가운 냄비로 열량이 전달됩니다. 열역학은 냄비와 같은 어떠한 계로 전달된 열량이 계 안에 있는 기체의 내부에너지로 바뀌거나 계가 주위로 일을 하게 되는 관계를 다루는 학문입니다.

정리하면 열량 Q란 뜨거운 물체에서 차가운 물체로 전달되는 에너지의 양입니다. 그렇다면 열량을 전달받은 계는 어떻게 될까요? 바로 (1)식의 열역학 제1법칙에 따라 기체의 내부에너지가 증가하거나 외부로 일을 하게 됩니다.

1-3. 일

계, 또는 기체가 일을 한다고 하는 것은 계의 부피, 즉 기체가 차지하고 있는 용기의 크기가 변하는 것을 말합니다. 예를 들어 공기가 들어있는 풍선이 있는데 풍선안의 공기 온도가 증가하면 풍선의 부피가 커지죠. 바로 이것이 기체가 일을 한 것입니다.

만일 풍선 내부의 압력 P가 일정한 상태에서 부피가 \Delta V만큼 변하면 풍선 내의 기체가 한 일은 다음 (5)식과 같이 정의됩니다.

\tag{5}
W = P \Delta V = P(V_f - V_i)

여기서 V_f는 풍선의 나중 부피이고 V_i는 처음 부피를 뜻합니다.

정리하면 계가 한 일 또는 기체가 한 일이 존재하기 위해서는 반드시 계의 부피가 변해야 합니다. 만일 부피가 변하지 않으면 한 일은 0입니다.

2. PV 도표

어떤 계의 열역학적 상태를 표현하기 위한 수단으로 PV 도표(또는 PV 다이어그램)가 활용됩니다.

이상기체의 상태방정식에 따르면 압력 P, 온도 T, 계의 부피 V사이에는 다음의 관계가 성립합니다.

\tag{6}
PV = nRT

이 식을 약간 정리하면 다음의 관계가 성립하죠.

\tag{7}
P \propto {T \over V}

아래 [그림 2]는 PV 도표를 나타냅니다.

[그림 2] PV 도표. PV도표를 사용하면 계의 압력, 부피, 온도에 대한 열역학적 상태를 하나의 점으로 표현할 수 있습니다. T_1에 비해 T_2의 온도가 더 높습니다.

(7)식에서와 같이 압력 P는 부피 V에 반비례하며 온도 T가 커질수록 원점으로부터 멀어지는 곡선이 그려집니다. 이러한 PV 도표를 사용하면 압력 P, 부피 V, 온도 T에 대한 열역학적 상태를 하나의 점으로 표현할 수 있습니다.

그렇다면 압력이란 무엇일까요? 마지막으로 압력 P에 대한 이야기를 하겠습니다.

이상기체가 들어있는 용기의 벽에 이상기체가 작용하는 압력은 다음과 같이 기술됩니다.

\tag{8}
P = {2 \over 3} \Big({N \over V} \Big) \Big( {1 \over 2} m \bar{v^2} \Big)

중요한 것은 압력 P는 분자의 평균운동에너지 KE에 비례하고 기체가 들어있는 용기의 부피 V에 반비례합니다.

\tag{9}
P \propto {KE \over V}

그래서 압력이 증가한다는 말은 부피 V가 일정할 때 분자의 운동에너지 KE가 증가하는 것을 뜻해요.

바꾸어 말하면 분자의 운동에너지 KE는 온도 T에 비례한다고 앞에서 설명드렸잖아요. 그래서 부피 V가 일정한 상태에서 용기의 온도 T가 상승하면 용기 내부 기체의 압력 P가 증가하게 됩니다.

또는 용기내 분자의 운동에너지 KE, 즉 용기의 온도 T가 일정하게 유지된다고 했을 때, 용기의 부피 V가 감소하면 압력 P는 증가하게 됩니다.

3. 등적 과정

등적 과정을 시작하기에 앞서 이것을 꼭 기억하세요.

첫째, 내부에너지가 증가한다는 말은 계의 온도가 증가하는 것을 말하며, 이것은 곧 기체 분자의 운동에너지가 증가되었음을 뜻한다.

둘째, 계의 압력이 증가한다는 말은 단위 부피당 기체의 운동에너지가 증가하는 것을 뜻한다.

셋째, 계 또는 기체분자가 일을 한다는 말은 계의 부피가 증가하는 것을 뜻한다.

이제 이번 글의 작성 목적인 등적과정에 대한 내용을 시작하겠습니다.

등적 과정 예시로는 부탄가스통이 뜨거운 불속에 놓여 있는 경우를 상상해 보세요. 물론 아주 위험한 상황이기는 한데요. 부탄가스통이 폭발하기 직전까지, 부피가 일정한 상태로 불꽃에서 가스통으로 열량이 계속 전달되고 있는 상황을 상상하면 됩니다.

3-1. 등적 과정에서의 분자운동

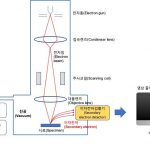
아래 [그림 3]은 온도가 T_1이며 부피가 고정된 용기내에 기체분자가 들어 있습니다. 그런데 이 용기가 온도 T_2인 열저장체와 접촉되었다고 생각해 보세요.

여기서 열저장체란 크기가 아주 커서 용기내의 기체 분자로 열량을 전달하더라도 온도가 떨어지지 않는 이상적인 물체를 말합니다. 보통의 경우 기체분자로 열량을 전달하면 열저장체의 온도가 하강하는 것이 보통입니다.

용기내의 온도가 T_1이므로 위에서 언급했듯이 온도에 비례하는 기체분자의 운동에너지는 KE_1으로 주어집니다.

운동에너지의 크기를 화살표 길이로 표기하면 훨씬 이해하기 쉬워요. 물론 운동에너지는 벡터량이 아니므로 화살표로 표기하는 것은 적절하지 않아요. 만일 이렇게 표현하는 것이 불편하다면 화살표를 분자의 속도벡터로 보아도 크게 상관 없어요.

[그림 3] 등적 과정. 기체가 들어 있는 용기의 부피 V는 고정되어 있습니다. 이때 차가운 온도 T_1의 기체분자가 들어 있는 용기가 뜨거운 온도 T_2와 열적으로 접촉되었습니다.

온도가 T_1인 수 많은 기체 분자중 어느 한개의 운동에너지를 화살표로 그린 것이 [그림 3]에서 용기내에 있는 왼쪽 화살표입니다. 그림과 같이 기체 분자는 열저장체를 향해 움직이고 화살표의 길이에 해당하는 운동에너지를 갖는 것으로 보아주세요.

그런데 이 기체 분자가 열저장체와 충돌하는 과정에서 뜨거운 열저장체로부터 열량 Q를 전달받아 온도가 충돌전 T_1에서 T_2로 상승하게 됩니다.

그러면 기체분자의 운동에너지는 [그림 3]의 오른쪽 화살표로 표현할 수 있어요.

충돌 전과 비교해 달라진 점은, 첫째 충돌 후에 운동방향이 반대로 바뀌었다는 것이고, 둘째 화살표의 길이, 즉 운동에너지의 크기가 더 길어졌어요. 즉 분자의 속력이 더 빨라진것이죠.

그러면 화살표의 길이는 얼마나 길어졌을까요? 그림과 같이 충돌과정에서 열저장체로부터 전달된 열량 Q만큼 화살표의 길이가 더 길어집니다.

그러므로 충분한 시간이 지난다면 용기내의 모든 기체 분자는 열저장체와 충돌을 계속하게 될거에요.

결국 용기내의 기체분자 온도는 T_1에서 모두 T_2로 바뀌게 되어 열저장체와 열평형상태가 될 것입니다.

등적과정은 바로 열저장체와 접촉한 후부터 열평형상태가 되기까지의 과정을 의미합니다.

3-2. 등적 과정에서의 열역학 제1법칙

그렇다면 이 등적과정에서 열역학 제1법칙은 어떻게 될까요?

우선 기체가 들어있는 용기를 열저장체와 접촉시긴 것은 우리가 행한 것이므로 열저장체로부터 용기를 향해 열량 Q가 계속 전달되고 있는 것은 확실합니다.

그렇다면 용기로 전달된 열량은 등적과정에서 어디에 사용될까요?

바로 [그림 3]과 같이 용기내의 기체분자가 열저장체와 충돌하는 과정중에 열량 Q를 전달 받아 자신의 운동에너지 KE를 상승시키는데 모두 사용됩니다. 즉, 전달된 열량은 기체분자의 운동에너지 KE를 증가시킵니다.

이것은 (4)식과 같이 기체 분자의 온도가 변한 것과 같고, 결과적으로 기체분자의 내부에너지 U가 변화되어 \Delta U가 0이 아님을 뜻합니다.

그렇다면 이번에는 기체분자가 한 일을 생각해 보겠습니다. 등적 과정은 기체분자가 들어있는 용기의 부피가 일정하게 유지되는 상태에서의 열역학적 과정입니다. 그러므로 부피가 전혀 변하지 않아요.

따라서 열량 Q를 받은 후의 부피와 받기 전의 부피가 동일하므로 (5)식에서 \Delta V가 0이 되어 한 일 W는 0이 됩니다.

결국 등적과정에서 전달된 열량 Q는 모두 기체 분자의 내부에너지 변화 \Delta U로 사용되므로 (1)식의 열역학 제1법칙은 다음의 관계를 갖습니다.

\tag{10}
\Delta U = Q

3-3. 등적 과정에서의 PV 도표

이번에는 등적 과정이 일어나는 동안 PV도표는 어떻게 달라지는지 보겠습니다.

아래 [그림 4]는 등적과정을 PV 도표에 그려낸 것입니다.

[그림 4] 등적 과정의 PV도표. A점이 B점으로 이동하는 것이 등적 과정입니다.

그림에서 A점이 B점으로 이동한 것이 등적과정을 나타냅니다. 즉 부피 V가 일정하게 유지된 상태에서 열저장체에 의해 기체분자의 온도가 T_1에서 T_2로 상승하여 A점이 B점으로 변화된 것이죠.

아울러 등적과정에서 y축의 압력이 상승하는 것을 볼 수 있는데요. 왜 용기내의 압력이 상승하게 될까요? 바로 (9)식을 참고하면 됩니다.

(9)식에 따르면 용기의 부피 V가 일정하게 유지된 상태에서 온도가 증가하면 기체분자들의 평균 운동에너지 KE가 증가하므로 압력 P가 증가하게 됩니다.

그래서 등적과정에서 압력이 증가할 수 밖에 없는 거에요.

이렇게 해서 등적과정에 대한 설명을 마칩니다. 등적과정이 일어나는 동안 압력, 부피, 온도의 상태변수(state variable)가 어떻게 변하는가를 설명드렸고, 열역학 제1법칙이 \Delta U = Q가 됨을 말씀드렸습니다. 다음 글에서는 등온과정을 다루겠습니다.

Related posts.

단위 변환 – 환산 인자만 알면 단위의 변환은 아주 쉬워 SEM 구조 – (2) 주사전자현미경의 전체적인 구조와 구성 주사 전자 현미경에서 ‘주사’란 무엇인가? 평균 – 산술, 기하, 조화 평균의 개념과 실생활 활용 등가소음도 연습 문제 차트 또는 그래프 만들때의 필수 구성 요소 두배각 공식 푸리에 급수 전개