Last Updated on 2024-01-06 by BallPen
미분방정식을 풀었을 때 나오는 해의 종류를 알아보겠습니다.
미분방정식 해(solution)의 종류에는 몇가지가 있을까요?
미분방정식을 공부하다 보면 다양한 해의 이름들이 나오는데요. 그 해의 특징들을 알아보겠습니다.
아래는 이번 글의 목차입니다.
Contents
참고로 말씀드리면 다양한 미분방정식 풀이 방법에 대한 글을 올리고 있습니다. 블로그 상단에 있는 검색창에 ‘미분방정식’이라고 입력해 보세요.
1. 미분방정식 해
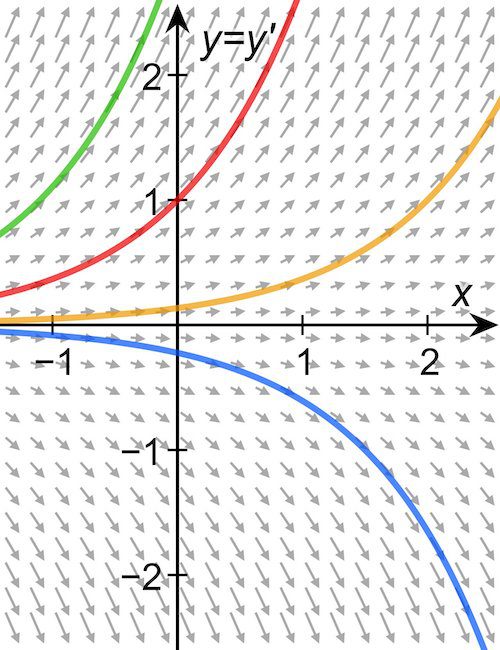
![[그림 1] <span class="katex-eq" data-katex-display="false">y=y^{\prime}={dy/dx}</span>의 미분방정식 해 <span class="katex-eq" data-katex-display="false">y=C \cdot e^{x}</span>에서 서로 다른 <span class="katex-eq" data-katex-display="false">C</span>값에 따른 곡선. <span class="katex-eq" data-katex-display="false">C</span>값이 무슨 값을 갖던 모두 미분방정식의 해가 됩니다. 이러한 해를 '일반해'라고 합니다. (그림 인용: wikimedia)](https://ballpen.blog/wp-content/uploads/2022/10/DGL_y-eq-dy-2.jpg)
함수 y=f(x)를 미분방정식에 대입했을 때, 그 방정식을 항등적으로 만족한다면 이 함수 y=f(x)를 ‘미분방정식의 해’라고 합니다.
또한 이러한 해를 구하는 과정을 ‘미분방정식을 푼다’라고 말합니다.
예를 들어 아래에 1계 1차 선형 상미분방정식이 있어요.
\tag{1}
\color{blue}{{dy}\over{dx}} = x이 방정식을 어떻게 풀어 내는지에 대한 방법은 나중에 고민하고요. 일단 아래 (2)식의 함수가 해가 될 수 있는지를 판정해보세요.
\tag{2}
\color{red}y = {1 \over 2} x^2판정을 위해서는 (2)식의 함수를 (1)식에 대입하여 우변과 항등관계가 성립하는지를 보면 됩니다.
\tag{3}
\begin{align}
{dy \over dx} &= {d \over dx}{\Big({1 \over 2} x^2 \Big)}\\
&= {1 \over \cancel2}(\cancel2x) \\
&= x
\end{align} 그 결과 (3)식과 같이 x가 도출되어 (1)식의 우변과 같은 값을 갖습니다. 따라서 (2)식은 (1)식의 해입니다.
그렇다면 아래의 (4)식도 (1)식에 주어진 미분방정식의 해일까요?
\tag{4}
\color{red}y = {1 \over 2} x^2 + 10같은 방법으로 (4)식을 (1)식에 대입하여 풀어보세요. 그 결과는 아래와 같습니다.
\tag{5}
\begin{align}
{dy \over dx} &= {d \over dx}{\Big({1 \over 2} x^2 + 10 \Big)}\\
&={d \over dx}\Big( {1 \over 2} x^2 \Big) + {d \over dx} (10)\\
&= {1 \over \cancel2}(\cancel2x) + 0\\
&= x
\end{align} 여기서도 x가 도출되어 (1)식의 우변과 같은 값을 갖습니다. 그러므로 (5)식의 함수도 (1)식의 해가 되는 것입니다.
이와 같이 미분방정식은 다양한 해가 존재할 수 있는데요. 이제부터 그 해의 종류에 대해 하나 하나 알아보겠습니다.
2. 미분방정식 해 종류
미분방정식의 해의 종류로는 일반해, 특수해, 특이해, 자명해로 구분할 수 있습니다.
2-1. 일반해 (general solution)
일반해는 미분방정식을 푸는 과정에서 도출된 상수 기호가 그대로 표시되어 있는 해를 말합니다. 따라서 상수에 어떠한 값이 들어가든 모두 해의 요건을 만족해요.
예를 들어 (1)식의 미분방정식을 풀면 다음의 해를 얻습니다. 여기서 이 해를 어떻게 구했는지는 당장 중요하지 않습니다. 나중에 다른 글에서 관련 내용을 기술하겠습니다.
아무튼 (1)식의 해는 다음 (6)식과 같이 도출됩니다.
\tag{6}
y= {1 \over 2} x^2 + C위 (6)식에서 C는 미분방정식을 푸는 과정에서 도입된 적분상수입니다. 말 그대로 상수이므로 어느 값이 들어가든 모두 미분방정식의 해가 될 수 있어요.
위에서 잠시 설명드렸던 (2)식은 C값이 0인 경우이고 (4)식은 10인 경우일 뿐입니다. 어떠한 값이 대입되어도 해가 됩니다.
이와 같이 적분상수가 표기되어 있는 해를 ‘일반해’라고 합니다.
결국 일반해는 상수 C가 무슨 값을 갖든 모두 성립하므로 (1)식의 미분방정식의 해는 무수히 존재할 수 있어요.
2-2. 특수해 (particular solution)
다시 말씀드리면 ‘일반해’란 미분방정식의 항등관계를 만족하는 상수조건을 갖는 어느 함수를 말합니다. 그래서 상수 조건에 따라 무수히 많은 해가 존재할 수 있어요.
따라서 그 수많은 해 가운데 무엇이 내가 구해야 할 해인지 궁금할 거에요. 수많은 해 중에 무엇이 진정한 해인지를 알기 위해서는 미분방정식을 푸는 사람이 ‘초기 조건(initial condition)’을 알아야 합니다.
여기서 초기 조건이란, 예를 들어 어떤 물체의 진동에 관한 미분방정식이 있다면 진동이 시작될 때 추가 어느 위치에 있었고 초기 속도는 얼마라고 하는 것들을 말합니다.
이러한 초기 조건을 일반해에 반영하면 수많은 해중 특수한 하나의 해를 도출할 수 있게 됩니다. 그리고 우리는 그것을 ‘특수해’라고 합니다.
예를 들어 보겠습니다.
\tag{7}
{dy \over dx} = 2x + 3(7)식의 미분방정식을 풀면 다음 (8)식의 일반해가 얻어집니다. 이때 이 미분방정식을 어떻게 풀었는지 궁금하겠지만 잠시만 미루어 두겠습니다. 일단 해의 종류에 대해서만 집중해서 보세요.
\tag{8}
y = x^2 + 3x + C(8)식에서 C는 상수로서 무슨 값이 들어가든 (7)식의 해가 됩니다. 이것을 ‘일반해’라고 이야기 했어요.
그러나 x가 1일때 y가 2가 된다는 y(1) = 2라는 초기 조건이 주어져 있다면 이 조건을 만족하는 특별한 해를 구할 수 있습니다. 바로 이 해가 ‘특수해’입니다.
이 초기 조건을 (8)식에 대입하면 상수 C의 특별한 값을 구할 수 있어요.
\tag{9}
\begin{align}
y(1) &= 2\\
y(1) &=1^2 + (3 \times 1) + C =2\\
C&=-2
\end{align}결국 y(1) = 2의 초기 조건을 만족하는 특별한 해, 즉 특수해는 다음과 같습니다.
\tag{10}
y= x^2 + 3x -2이러한 특수해는 자연과학 및 공학문제의 해를 구하는 과정에서 아주 중요하게 간주됩니다. 물론 일반해에서 나타나는 미지수 갯수 만큼의 초기 조건이 있어야 특수해를 구할 수 있습니다.
이와 같이 일반해를 구한 후 초기 조건을 적용하여 특수해를 구하는 것을 초기값 문제(initial value problem)라고 한답니다.
2-3. 특이해 (singular solution)
미분방정식을 풀면 일반해가 도출됩니다. 그리고 초기 조건을 적용하면 특수해를 구할 수 있어요.
그러나 어떤 미분방정식은 일반해와 특수해의 형태를 갖지 않는 특이한 해도 존재합니다. 이 해를 ‘특이해’라고 부릅니다.
예를 들어 아래의 미분방정식이 있다고 생각해봐요.
\tag{11}
\Big[\Big({dy \over dx}\Big)^2 - x \Big({dy \over dx} \Big) \Big] + y =0미분방정식을 푸는 표준화된 방법으로 (11)식의 해를 구하면 다음 (12)식의 일반해가 얻어집니다.
\tag{12}
y = cx -c^2이때 c 는 무슨 값이 들어가도 되는 상수입니다. 이 식이 해가 되는지의 여부는 (12)식을 (11)식에 대입하여 풀어보면 좌변이 0이 되어 우변의 0과 항등관계를 만족함을 알 수 있어요.
그런데 (11)식의 미분방정식은 다음 (13)식도 해가 됨을 알 수 있어요.
\tag{13}
y = {1 \over 4} x^2위 (13)식을 (11)식에 대입해서 풀어보세요.
\tag{14}
\begin{align}
\Big[\Big({dy \over dx}\Big)^2 - x \Big({dy \over dx} \Big) \Big] + y &=0\\
\Big( {1 \over 2}x\Big)^2 - x\Big({1 \over 2} x \Big) + {1 \over 4} x^2 &= 0 \\
0&=0
\end{align}그러면 (14)식의 좌변과 우변이 모두 0의 항등관계를 만족하므로 (13)식도 해가 됨을 알 수 있어요.
이와 같이 미분방정식 풀이로 얻어지는 일반해(또는 특수해)와는 다르게 특이하게 존재하는 해를 ‘특이해’라고 합니다.
2-4. 자명해 (trivial solution)
자명해는 특이해와 비슷한 성격을 갖습니다.
다만, 특이해는 직관적으로 파악하기 어려운 특이한 해이지만. 자명해는 누가 봐도 직관적으로 빠르게 알아낼 수 있는 해를 ‘자명해’라고 합니다.
아래의 미분방정식을 보아주세요.
\tag{15}
{d^2 y \over dx^2} -2 {dy \over dx} +y =0직관적으로 볼 때 해가 될 수 밖에 없는 해는 y=0입니다. y=0을 (15)식에 대입해보세요.
자명하게 0이 되는 것을 알 수 있어요. 이러한 해를 ‘자명해’라고 합니다.





7 thoughts on “미분방정식 해 종류 : 일반해, 특수해, 특이해, 자명해”