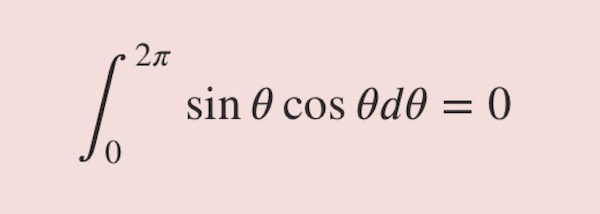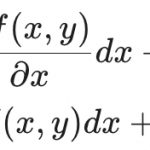Last Updated on 2025-08-06 by BallPen
사인과 코사인 곱을 한 주기에 걸쳐 적분해 봐요.
사인과 코사인 곱의 적분 계산을 위해서는 부분적분법을 사용하면 편리해요.
1. 부분적분법
부분적분법 공식은 다음과 같아요.
\begin{align}
\tag{1}
\int_a^b u {v}’ d \theta = \Big[uv\Big]_a^b – \int_a^b u’ v d\theta
\end{align}
2. 사인과 코사인 곱의 적분
이제 사인과 코사인 곱의 적분을 알아 봐요. 즉, 다음의 적분을 계산해 보자는 거에요.
\begin{align}
\tag{2}
\int_0^{2\pi} \sin \theta \cos \theta d \theta
\end{align}
(2)식을 적분하기 위해 부분적분법을 적용해봐요. 이를 위해 \(\sin \theta = u\)로 \(\cos \theta = v’\)으로 생각합니다. 그리고 (1)식을 적용하면 아래와 같아요.
\begin{align}
\tag{3}
\int_0^{2 \pi} \sin \theta \cos \theta d \theta = \Big[ \sin \theta \sin \theta \Big]_0^{2 \pi} – \int_0^{2 \pi} \cos \theta \sin \theta d \theta
\end{align}
윗 식에서 적분기호가 있는 항을 좌변으로 몰고 정리하면 다음과 같아요.
\begin{align}
\tag{4}
2 \int_0^{2 \pi} \sin \theta \cos \theta d \theta &= \sin^2(2 \pi) – \sin^2 (0)\\[8pt]
&=0
\end{align}
따라서 사인과 코사인 곱의 적분은 다음과 같다는 것을 알 수 있습니다.
\begin{align}
\tag{5}
\int_0^{2\pi} \sin \theta \cos \theta d\theta =0
\end{align}