Last Updated on 2024-01-15 by BallPen
벡터끼리 곱하는 한 방법으로 외적이 있습니다. 외적을 하면 그 결과 값은 벡터가 됩니다.
외적(Vector product, Cross product)은 내적(Scalar product, Dot product)과 같이 벡터와 벡터를 곱하는 또 하나의 방법입니다.
차이가 있다면 두 벡터를 내적하면 그 결과가 스칼라가 나오지만 외적하면 벡터가 나옵니다. 그래서 외적을 다른 말로 ‘벡터곱’이라고도 부릅니다.
의외로 계산 방법이 아주 재미있어요. 함께 알아봐요.
아래는 이번 글의 목차입니다.
Contents
1. 내적 복습
외적을 알아보기 전에 내적을 잠시만 복습하겠습니다. 그래야 내적과 외적의 차이를 쉽게 구분할 수 있을 거에요.
벡터 A와 벡터 B가 있을 때 그 두 벡터를 내적하면 다음과 같습니다.
\tag{1}
\begin{align}
\vec A \cdot \vec B = AB \cos \theta
\end{align}여기서 A와 B는 두 벡터의 크기입니다. 그리고 \theta는 두 벡터 사이의 사이각을 말하죠.
따라서 벡터 \vec A와 벡터 \vec B가 서로 평행하면 (1)식은 다음과 같이 표현될 수 있어요.
\tag{2}
\begin{align}
\vec A \cdot \vec B &= AB \cos \theta\\
&= AB \cos 0 ^\circ\\
&=AB
\end{align}반대로 두 벡터가 서로 수직하면 다음과 같이 표현됩니다.
\tag{3}
\begin{align}
\vec A \cdot \vec B &= AB \cos \theta\\
&= AB \cos 90 ^\circ\\
&=0
\end{align}이 성질을 이용해 어느 두 벡터가 수직한지의 여부를 알고 싶다면 두 벡터를 내적해봐서 0이 나오는지를 확인하면 됩니다.
성분법으로 내적을 표현하면 다음과 같습니다.
벡터 \vec A = A_x \hat x + A_y \hat y + A_z \hat z와 벡터 \vec B = B_x \hat x + B_y \hat y + B_z \hat z를 내적하는 예시입니다.
\tag{4}
\begin{align}
\vec{A} \cdot \vec{B} &= (A_x \hat x + A_y \hat y + A_z \hat z) \cdot (B_x \hat x + B_y \hat y + B_z \hat z)\\
&=A_x B_x + A_y B_y + A_z B_z
\end{align}또한 내적은 교환법칙과 분배법칙이 성립합니다.
마지막으로 내적이 사용되는 대표적 사례가 일정한 힘 \vec F가 작용하여 물체를 변위 \vec x만큼 이동시켰을 때 한 일 W를 표현하는데 사용될 수 있어요.
\tag{5}
\begin{align}
W = \vec F \cdot \vec x = Fx \cos \theta
\end{align}(5)식과 같이 내적을 이용해 일을 표현함으로써 \vec F와 \vec x가 주어지면 각도 \theta에 따라 한 일의 크기를 손쉽게 구할 수 있어요.
2. 외적 정의
2-1. 기하학적 의미
외적도 내적과 마찬가지로 벡터와 벡터를 곱하는 방법의 한 종류입니다.
외적의 결과는 벡터이기 때문에 ‘벡터곱’이라고도 하고, 외적 기호로서 \times가 사용되기 때문에 ‘크로스 곱’이라고도 불립니다.
내적은 한 벡터에 다른 벡터를 투영한 후 그 크기를 곱한다고 말씀드렸어요.
이에 비해 외적은 두 벡터가 만드는 평행사변형 면적이 외적의 크기가 되고, 외적의 방향은 평행사변형에 수직인 방향으로 정의합니다.
사실 이렇게 정의하는 이유는 자연계에서 나타나는 여러 물리 현상들이 외적의 규칙에 부합하는 것들이 존재하기 때문이에요.
이에 대한 예시는 아래쪽에 따로 설명 드리겠습니다.
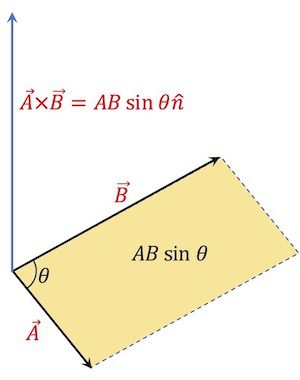
아래 [그림 1]은 두 벡터 \vec A와 \vec B를 외적했을 때 갖게 되는 크기와 방향을 보여주고 있어요.
![[그림 1] 벡터의 외적. 두 벡터를 외적하면 외적한 벡터의 크기는 평행사변형의 면적이 되고 방향은 평행사변형에 수직한 방향입니다.](https://ballpen.blog/wp-content/uploads/2022/12/Picture1-3-807x1024.jpg)
이를 식으로 표현하면 다음과 같습니다. 여기서 외적의 연산 기호 \times를 임의로 없애거나 \cdot으로 바꾸면 절대 안됩니다.
\tag{6}
\begin{align}
\vec A \times \vec B = AB \sin \theta~ \hat n
\end{align}(6)식에서 A와 B는 두 벡터의 크기이고, \theta는 두 벡터 사이의 각도입니다. 또한 \hat n은 두 벡터가 만드는 평면에 수직한 방향의 단위벡터입니다.
여기서 잘 보시면 AB \sin \theta는 평행사변형의 면적과 같아요.
만일 \theta가 90^{\circ}이면 직사각형 면적이되고, \theta가 0^{\circ}이면 면적이 0이 됩니다. 그래서 외적의 크기는 두 벡터가 만드는 평행사변형 면적과 같아요.
외적의 결과는 벡터이므로 크기와 방향을 모두 같습니다. 그렇다면 방향은 어느쪽일까요?
바로 [그림 1]에 표시한것처럼 방향은 두 벡터가 만드는 평면에 수직한 방향으로 잡습니다.
여기서 많은 분들이 왜 외적의 방향을 수직한 방향으로 잡았는지 궁금해하는 분들이 계셔요. 그 이유는 위에서 잠시 말씀드렸듯이 외적의 형식으로 나타나는 물리 현상들이 있어요.
그러한 현상들은 외적의 방향을 두벡터가 만드는 평면에 수직한 방향으로 설정해야 설명이 되기 때문입니다.
[외적 방향: 오른손 법칙]
아울러 평행사변형의 면적에 수직한 방향이 [그림 1]에 표시한 방향도 있지만 그 반대방향도 있다는 것을 알 수 있어요. 그래서 외적의 방향은 오른손 법칙을 따르는 것으로 정했어요.
오른손 법칙은 아래의 [그림 2]를 참고하세요. 우선 오른손 손바닥을 쫙 펴세요.
그리고 두번째 손가락(검지)부터 새끼 손가락(소지)까지를 서로 붙인 후 그 손가락들로 벡터 \vec A를 시작으로 벡터 \vec B를 감아쥔 후 엄지손가락을 위로 펴면 그 엄지손가락의 방향이 외적 \vec A \times \vec B의 방향이 됩니다.
![[그림 2] 외적 방향을 결정하는 오른손 법칙 (그림인용: Public Domain Pictures Net)](https://ballpen.blog/wp-content/uploads/2022/12/Picture11.jpg)
만일 벡터 \vec B를 시작으로 벡터 \vec A를 감은 후 엄지손가락을 펴면 그 엄지손가락의 방향은 [그림 2]와는 반대가 됩니다.
이때는 \vec B \times \vec A가 됩니다.
2-2. 수학적 계산
[성분법]
성분법으로 표기된 두 벡터를 수학적으로 외적하는 방법입니다. 기본적으로 (6)식의 개념을 그대로 적용하니 어렵지 않아요.
그렇지만 꼭 볼펜을 잡고 종이에 한번은 꼭 풀어보세요. 외울 필요는 전혀 없지만 한번은 해봐야 외적에 대한 자신감이 생겨요.
벡터 \vec A = A_x \hat x + A_y \hat y + A_z \hat z와 벡터 \vec B = B_x \hat x + B_y \hat y + B_z \hat z를 외적하면 다음과 같습니다.
\tag{7}
\begin{align}
\vec A \times \vec B &=(A_x \hat x + A_y \hat y + A_z \hat z) \times (B_x \hat x + B_y \hat y + B_z \hat z )\\
&= A_x B_x (\hat x \times \hat x) + A_x B_y (\hat x \times \hat y) + A_x B_z (\color{red}\hat x \times \hat z \color{black})\\
&~~~+A_y B_x (\color{red}\hat y \times \hat x \color{blackr}) + A_y B_y (\hat y \times \hat y) + A_y B_z (\hat y \times \hat z)\\
&~~~+A_z B_x (\hat z \times \hat x) + A_z B_y (\color{red}\hat z \times \hat y \color{black}) + A_z B_z (\hat z \times \hat z)\\
&=A_x B_x (1\cdot1 \cdot\sin 0^\circ) + A_x B_y (1 \cdot 1 \cdot \sin 90^\circ \hat z) + A_x B_z (1 \cdot1\cdot\sin(90^\circ)(\color{red}{-\hat y} \color{black} ))\\
&~~~+A_y B_x (1 \cdot1\cdot \sin 90^\circ (\color{red}- \hat z\color{black})) + A_y B_y (1 \cdot 1\cdot\sin0^\circ) + A_y B_z (1 \cdot 1 \cdot\sin90^\circ \hat x)\\
&~~~+A_z B_x (1 \cdot 1 \cdot \sin90^\circ \hat y) + A_z B_y (1 \cdot 1 \cdot \sin 90^\circ (\color{red}-\hat x \color{black})) + A_z B_z (1 \cdot 1 \cdot 0^\circ)\\
&=0+A_x B_y \hat z + A_x B_z(- \hat y) +A_y B_x (- \hat z) + 0 + A_y B_z \hat x +A_z B_x \hat y + A_z B_y (-\hat x) + 0\\
&=(A_y B_z - A_z B_y) \hat x + (A_z B_x - A_x B_z)\hat y + (A_x B_y - A_y B_x)\hat z
\end{align}식 (6)의 첫번째 줄을 전개하면 두번째 줄처럼 쓸수 있어요.
이때 벡터의 크기는 그냥 곱하면 됩니다. 다만 단위벡터끼리의 외적은 (6)식의 규칙을 적용합니다. 예를 들어 \hat x \times \hat x는 크기가 모두 1이고 방향이 x방향인 단위벡터의 외적입니다.
따라서 (6)식을 적용하면 1 \cdot 1 \cdot \sin 0^{\circ} = 0이 됩니다. 둘다 x방향으로 평행한 단위벡터끼리의 외적이므로 결과값은 0이될 뿐이에요.
\hat x \times \hat y는 어떨까요? (6)식과 [그림 2]를 적용하면 1 \cdot 1 \cdot \sin 90^{\circ} \hat z = \hat z가 됩니다.
그렇다면 \hat x \times \hat z는 어떨까요? (6)식과 [그림 2]를 적용하면 1 \cdot 1 \cdot \sin 90^{\circ} (-\hat y) = -\hat y이 됩니다. 이때 \hat y앞에 음수가 붙는 이유는 \hat z \times \hat x가 \hat y 인데 그것의 반대방향으로 주어지기 때문입니다.
꼭 [그림 2]와 같이 오른손을 움직여가며 방향을 찾는 연습을 해보세요. 아니면 아래 [그림 3]의 방법을 사용해도 됩니다.
![[그림 3] 단위벡터 외적 계산에서 방향 결정하는 법](https://ballpen.blog/wp-content/uploads/2022/12/Picture21.jpg)
[그림 3]의 왼쪽 그림은 \hat x , ~ \hat y, ~ \hat z가 반시계방향으로 서로 곱해질 때 외적 결과의 방향을 나타냅니다. 오른쪽 그림은 단위벡터가 시계방향으로 곱해질 때 외적 결과의 방향이 음수가 됨을 나타내고 있어요.
[그림 2]의 오른손 법칙으로도 외적 방향을 결정하는데 큰 문제는 없으나, 간혹 헷갈릴 때는 [그림 3]을 그려보며 외적 방향을 결정하면 좋아요.
[행렬 표현법]
앞의 (7)식에서 외적은 다음과 같이 계산된다는 것을 알았어요.
\tag{8}
\begin{align}
\vec A \times \vec B &=(A_y B_z - A_z B_y) \hat x + (A_z B_x - A_x B_z)\hat y + (A_x B_y - A_y B_x)\hat z
\end{align}그런데 (8)식의 우변과 같이 외적의 결과를 표현하니 너무 길고 쓰기가 번거로워요. 그리고 이것을 외우는 것도 쉬운 일이 아니에요.
그래서 외적을 행렬식의 형태로 간결하게 표현하기도 합니다. 이번에는 그 방법을 알아봐요.
확실한 것은 (8)식으로 표현하는 것보다 더 쉬워요. 요령만 안다면요.
벡터 \vec A = A_x \hat x + A_y \hat y + A_z \hat z와 벡터 \vec B = B_x \hat x + B_y \hat y + B_z \hat z의 외적을 행렬식의 형태로 표현하면 다음과 같습니다.
\tag{9}
\begin{align}
\vec A \times \vec B =
\begin{vmatrix}
\hat x & \hat y & \hat z\\
A_x & A_y & A_z \\
B_x & B_y & B_z
\end{vmatrix}
\end{align}어떠신가요? (9)식이 (8)식과 같아보이나요?
(9)식을 보시면 1행에 단위벡터를, 2행에 벡터 \vec A의 각 성분을, 3행에 벡터 \vec B의 각 성분을 순서대로 나열한 거에요.
(8)식과 (9)식이 많이 달라보이지만 외적을 공부한 사람은 두 식이 같다는 것을 알고 있습니다.
그렇다면 이 두 표현이 같기 위해서는 (9)식이 (8)식과 동일하게 표현되는 방법을 이해하면 될거에요.
이제부터 시작할께요. 아래 [그림 4]를 보아 주세요.
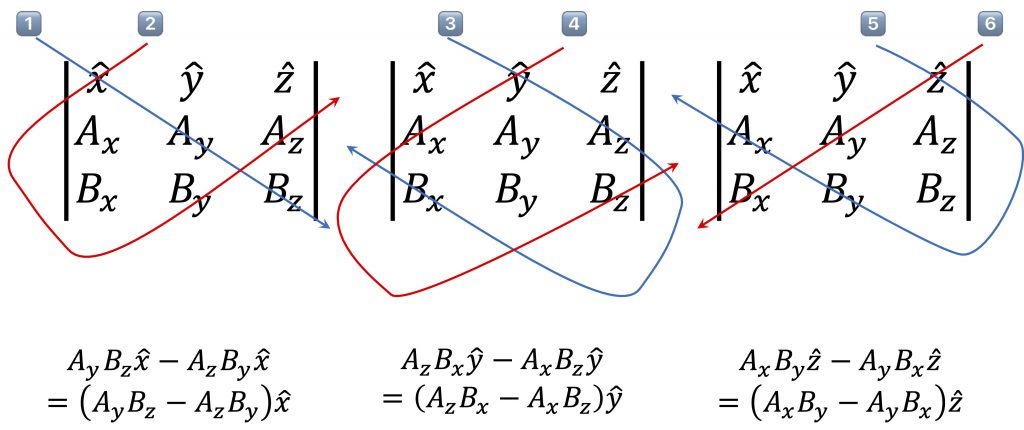
[그림 4]를 보시면 파랑색 선은 단위벡터 \hat x, \hat y, \hat z를 각각 출발해서 대각선 오른쪽 아래방향으로 총 3개의 성분씩 곱해지는 것을 나타내요.
비슷한 방법으로 빨강색 선은 단위벡터 \hat x, \hat y, \hat z를 각각 출발해서 대각선 왼쪽 아래방향으로 총 3개의 성분씩 곱해 집니다.
그리고 파랑색 선으로 곱해진 값에서 빨강색 선으로 곱해진 값을 빼면 [그림 4]의 아래쪽 수식이 만들어져요.
그리고 그 수식들을 모두 합하면 바로 (8)식으로 귀결되는 것을 알 수 있습니다.
다소 복잡해 보이지만 볼펜을 들고 직접 전개해보면 생각보다는 쉽게 할 수 있어요. 그리고 이 방법에 익숙해지면 (8)식을 외우지 않아도 외적에 관한 식을 언제든지 도출할수 있어요.
대부분의 사람들도 (8)식보다는 [그림 4]의 행렬식 표현법을 더 선호한답니다. 외울필요도 없고 간결하니까요.
3. 외적 예제 풀이
(예제) [그림 5]와 같이 사이각 \theta를 갖는 두 벡터 \vec A = A_x \hat x와 \vec B = B_x \hat x + B_y \hat y가 있다. 이 두 벡터의 외적 결과가 AB\sin \theta \hat z로 주어짐을 보여라.
![[그림 5] 외적 계산에 대한 예제](https://ballpen.blog/wp-content/uploads/2022/12/Picture81-1-1024x842.jpg)
(풀이) 문제에서 \vec A는 A_x \hat x로 주어져 있어요. 벡터 \vec B의 경우 B_x \hat x + B_y \hat y로 주어져 있습니다.
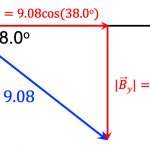
이때 [그림 5]를 보면 B_x는 B \cos \theta와 길이가 같고, B_y는 B \sin \theta와 같아요. 이를 반영하면 두 벡터는 다음과 같이 다시 쓸 수 있어요.
\tag{q-1}
\begin{align}
\vec A &= A_x \hat x = A \hat x + 0 \hat y + 0 \hat z\\
\vec B &= B_x \hat x + B_y \hat y = B \cos \theta \hat x + B \sin \theta \hat y + 0 \hat z
\end{align}(8)식이나 (9)식을 이용하여 이 두벡터를 외적하면 다음과 같습니다.
\tag{q-2}
\begin{align}
\vec A \times \vec B &=
\begin{vmatrix}
\hat x & \hat y & \hat z\\
A & 0 & 0\\
B\cos \theta & B\sin \theta & 0
\end{vmatrix}\\
&=(0-0)\hat x + (0-0)\hat y + (AB\sin \theta -0)\hat z\\
&=AB \sin \theta \hat z
\end{align}4. 외적의 성질
4-1. 교환법칙 불성립
외적은 위에서 설명드렸듯이 두 벡터를 서로 교환하여 곱하면 결과값이 달라집니다. 외적 결과 벡터의 크기는 같지만 방향이 반대가 되기 때문에 앞에 음의 부호가 붙게 됩니다.
이것을 꼭 명심해야 합니다.
\tag{10}
\begin{align}
\vec A \times \vec B &\ne \vec B \times \vec A\\
\vec A \times \vec B &= -(\vec B \times \vec A)\\
\end{align}4-2. 분배법칙 성립
외적에 대한 분배 법칙이 성립합니다.
\tag{11}
\vec A \times (\vec B + \vec C) = \vec A \times \vec B + \vec A \times \vec C4-3. 결합법칙 불성립
아래 (12)식처럼 외적에서 결합법칙은 성립하지 않습니다. 꼭 조심하셔야 해요.
이러한 관계를 벡터 삼중곱의 비결합성이라고도 말합니다.
\tag{12}
\vec A \times (\vec B \times \vec C) \ne (\vec A \times \vec B) \times \vec C4-4. 두 벡터가 수직하면 외적 벡터의 크기가 최대
두 벡터를 외적한 결과값이 최대가 되기 위해서는 두 벡터가 수직해야 합니다. 그 이유는 두 벡터의 사이각이 90^{\circ}가 되면 (6)식에서 \sin 90^{\circ} = 1이 되기 때문입니다.
4-5. 두 벡터가 평행하면 외적한 값은 0
두 벡터를 외적한 결과값이 0이 나오면 두 벡터는 평행하다는 의미입니다. 그 이유는 두 벡터의 사이각이 0^{\circ}가 되면 (6)식에서 \sin 0^{\circ} = 0이 되기 때문입니다.
5. 외적의 활용 사례 (외적을 하는 이유)
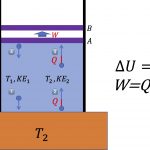
자기장 \vec B=2.50~\mathrm{T}내에서 속도 \vec v = 8.00 \times 10^6~ \mathrm{m/s}로 움직이는 양의 전하 +q = 1.60 \times 10^{-19}~\mathrm{C}가 받는 자기력 \vec F의 크기와 방향은 어떨까요? 이때 전하가 움직이는 방향과 자기장 사이의 각도는 60^{\circ}입니다.
![[그림 6] 자기력을 받는 움직이는 전하](https://ballpen.blog/wp-content/uploads/2022/12/Picture91-1006x1024.jpg)
실험에 의하면 이 경우 전하가 받는 힘은 \vec v의 방향도 아니고 \vec B의 방향도 아닙니다. 놀랍게도 \vec v와 \vec B가 만드는 평면에 수직한 방향으로 자기력이 작용합니다.
결국 전하가 받는 자기력의 크기는 qvB \sin \theta이고 방향은 \hat z입니다. 이를 식으로 쓰면 다음과 같아요.
\tag{13}
\begin{align}
\vec F_B = q (\vec v \times \vec B)=qvB\sin \theta \hat z
\end{align}(13)식에서 중요한 것은 외적이 사용되는 경우가 자연계에서 존재한다는 거에요. 그래서 외적 계산 방법을 알아야 합니다.
문제에 주어진 값들을 (13)식에 대입하면 자기력의 크기는 다음과 같습니다.
\tag{13}
\begin{align}
|\vec F_B| &= |q (\vec v \times \vec B)|\\
&= q vB \sin \theta\\
&=(1.60 \times 10^{-19}~\mathrm{C})(8.00 \times 10^6 ~\mathrm {m/s})(2.50~\mathrm{T})(\sin 60^{\circ})\\
&=2.77 \times 10^{-12}~\mathrm{N}
\end{align}

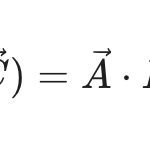
안녕하세요, 쓰신 글들 정말 큰 도움이 되었습니다!
그런데 궁금한것이, 식 (6)의 첫번째 줄에 (A벡터)+(B벡터)라 쓰여있는데, +가 아니라 X여야 하지 않나 싶어서요. 오타인지 아니면 제가 잘못 이해한 걸까요?
Yoon Lee님의 말씀이 맞습니다. 제가 틀렸어요.
해당 오타를 바로 수정하였습니다.
Yoon Lee님 처럼 큰 도움 주시는 분들이 계셔서 항상 감사한 마음 갖고 있습니다.
감사합니다.
아울러 수식 번호 일부가 중복된게 발견되어 수식 번호 순서도 수정하였습니다. 이에 따라 말씀하신 (6)식이 (7)식으로 변경되었습니다.
참고하세요.