Last Updated on 2025-09-10 by BallPen
자기에 대한 가우스 법칙으로 불리는 자기장의 발산에 대해 알아 봐요.
자기장의 발산 \nabla \cdot \vec B을 구해 보겠습니다. 이 개념은 자기장의 특성을 이해하는데 아주 중요합니다.
결론부터 말씀드리면 자기장의 발산은 0입니다.
\begin{align}
\tag{D1}
\nabla \cdot \vec B =0
\end{align}그리고 윗 식에 발산 정리를 적용하면 다음 식이 성립합니다. 즉 닫혀진 곡면에 대한 자기장 선속은 0입니다.
\begin{align}
\tag{D2}
\oint \vec B \cdot d \vec a = 0
\end{align}가우스 법칙으로 설명되는 전기장의 발산과 비교하면 재미있을 거에요. 전기장의 발산과 달리 자기장의 발산이 0이라는 것은 N극과 S극의 독립적 자기홀극이 존재하지 않음을 의미합니다.
1. 부피 전류에 대한 비오-사바르의 법칙
비오-사바르의 법칙은 정상전류가 흐를 때 자기장을 구하는 법칙인데요.
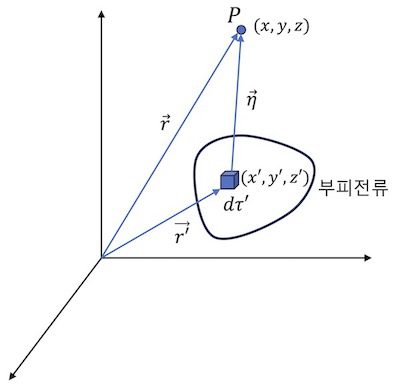
![[그림 1] 부피전류가 흐르는 미소 부피요소로부터 <span class="katex-eq" data-katex-display="false">\vec \eta</span>만큼 떨어진 지점이 <span class="katex-eq" data-katex-display="false">P</span>입니다.](https://ballpen.blog/wp-content/uploads/2025/09/Picture1-1-1024x994.jpg)
위 [그림 1]과 같이 부피 전류에 의한 P점에서의 자기장은 비오-사바르 법칙에 따라 다음 (1-1)식과 같이 주어집니다.
\begin{aligned}
\tag{1-1}
\vec B(\vec r) = {{\mu_0}\over{4 \pi}}\int {{\vec J(\vec {r^{\prime}})\times\hat \eta}\over{\eta^2}} d\tau^{\prime}
\end{aligned}여기서 \mu_0 = 4 \pi \times 10^{-7}~{\rm N / A^2}으로 진공중의 투자율이라고 합니다. 그리고 \vec J(\vec r^{\prime})은 전류밀도로서 단위면적당 흐르는 전류입니다.
한편 벡터 \vec \eta는 다음의 관계에 있습니다.
\begin{aligned}
\tag{1-2}
\vec \eta &= \vec r - \vec r^{\prime}\\[10pt]
&=(x\hat x + y\hat y + z\hat z) - (x^{\prime} \hat x + y^{\prime} \hat y+z^{\prime} \hat z)\\[10pt]
&=(x-x^{\prime}) \hat x+(y-y^{\prime}) \hat y+(z-z^{\prime}) \hat z
\end{aligned}그러므로 벡터 \vec \eta의 크기는 다음과 같아요.
\begin{align}
\tag{1-3}
\eta = \sqrt{(x-x^{\prime})^2+(y-y^\prime)^2+(z-z^{\prime})^2}
\end{align}2. 자기장의 발산
자기장의 발산을 구하기 위해 (1-1)식의 형태를 다음과 같이 바꾸어 봐요. \eta는 스칼라이므로 어느쪽에 곱해져도 상관없겠죠.
\begin{align}
\tag{2-1}
\vec B (\vec r) = {{\mu_0}\over{4 \pi}} \int \vec J (\vec r^{\prime}) \times {\color{blue}{{\hat \eta}\over{\eta^2}}} d \tau^{\prime}
\end{align}그러면 윗 식에서 파랑색 수식을 볼 수 있는데요. 이것은 아래 (2-2)식으로 표현되는 1/\eta의 기울기와 같다는 것을 알 수 있습니다.
\begin{align}
\tag{2-2}
\nabla \Big({1 \over {\eta}}\Big) = - {{\hat \eta}\over{\eta^2}} = - \nabla^{\prime} \Big({1 \over{\eta}}\Big)
\end{align}위 (2-2)식을 (2-1)식에 대입하면 다음과 같아진다는 것을 알 수 있어요. 이때 음의 부호는 제일 앞으로 빼냈습니다.
\begin{align}
\tag{2-3}
\vec B (\vec r) = -{{\mu_0}\over{4 \pi}} \int {\color{red}\vec J (\vec r^{\prime}) \times \nabla \Big({1\over{\eta}}\Big)} d \tau^{\prime}
\end{align}또한 윗 식에서 빨강색 수식 부분을 잘 보면 벡터 미분 연산자를 이용한 일계 미분 곱셈 규칙 중 다음 (2-5)식의 빨강색 부분과 같은 형태임을 알 수 있어요.
\begin{align}
\tag{2-4}
\nabla \times (f \vec v) = (\nabla f) \times \vec v + f(\nabla \times \vec v)
\end{align}\begin{align}
\tag{2-5}
\nabla \times (f \vec v) = (\nabla f) \times \vec v -{\color{red} (\vec v \times \nabla f)}
\end{align}참고로 (2-4)식에서 (2-5)식으로 넘어갈 때 외적은 교환법칙이 불성립하기 때문에 곱셈 순서를 바꾸면 음수가 붙습니다. 그리고 어떤 벡터 \vec v를 먼저 회전한 후 스칼라함수 f와 곱하던 , f의 기울기를 취한 후 벡터와 외적을 하던 결과는 같습니다.
(2-5)식의 관계를 (2-3)식에 반영하면 다음 식이 성립합니다.
\begin{aligned}
\tag{2-6}
\vec B (\vec r) &= -{{\mu_0}\over{4 \pi}} \int \Big({\nabla {1 \over \eta}}\times \vec J(r^{\prime})\Big)-\Big(\nabla \times{{\vec J(r^\prime)}\over{\eta}}\Big) d \tau^{\prime}\\[10pt]
&= -{{\mu_0}\over{4 \pi}} \int {1 \over \eta}{\Big(\color{blue}{\nabla }\times \vec J(r^{\prime})}\Big)-\Big(\nabla \times{{\vec J(r^\prime)}\over{\eta}}\Big) d \tau^{\prime}\\[10pt]
\end{aligned}이때 윗 식의 파랑색 부분은 0이 됩니다. 왜냐면 \vec J(r^\prime)은 r^{\prime}만의 함수인데 이를 r의 함수로 미분하기 때문입니다.
그래서 결국 (2-6)식은 다음과 같아져요.
\begin{aligned}
\tag{2-7}
\vec B (\vec r) &= {{\mu_0}\over{4 \pi}} \int \Big(\nabla \times{{\vec J(r^\prime)}\over{\eta}}\Big) d \tau^{\prime}\\[10pt]
\end{aligned}이때 적분은 프라임 좌표계에 대해서만 적분하면 되므로 비프라임 좌표계로 미분하는 \nabla는 적분 기호 밖으로 나올 수 있습니다.
\begin{aligned}
\tag{2-8}
\vec B (\vec r) &= {{\mu_0}\over{4 \pi}} \Big(\nabla \times\int {{\vec J(r^\prime)}\over{\eta}} d \tau^{\prime}\Big)\\[10pt]
\end{aligned}이제 이 글의 목적인 자기장의 발산을 구할 건데요. 위 식의 양변에 발산을 취해 봐요. 그러면 다음과 같습니다.
\begin{aligned}
\tag{2-9}
\nabla \cdot\vec B (\vec r) &= {{\mu_0}\over{4 \pi}}\nabla \cdot \Big(\nabla \times\int {{\vec J(r^\prime)}\over{\eta}} d \tau^{\prime}\Big)\\[10pt]
\end{aligned}그런데 여기서 윗 식의 우변 형태를 잘 보면 적분으로 구해지는 벡터가 있을텐데요. 그 벡터에 회전을 취하고 다시 발산을 구하는 연산임을 알 수 있습니다.
그런데 벡터 미분 연산자를 이용한 이계 미분 곱셈 규칙 중 아래 (2-10)식과 같이 회전의 발산 연산은 0이 되어 버립니다.
\begin{align}
\tag{2-10}
\nabla \cdot (\nabla \times \vec v) =0
\end{align}결국 이에 따라 (2-9)식의 우변도 0이 됩니다. 결국 자기장의 발산은 아래 (2-11)식과 같이 0입니다.
\begin{align}
\tag{2-11}
\nabla \cdot \vec B =0
\end{align}3. 자기장 선속
(2-11)식을 부피적분하고 발산정리를 적용하면 아래와 같아요.
\begin{align}
\tag{3-1}
\int_V (\nabla \cdot \vec B)d\tau = \oint\vec B \cdot d \vec a =0
\end{align}즉 닫힌 곡면에서 자기장 선속은 0이 되는데요. 이것을 자기에 대한 가우스법칙이라고 합니다.
이것은 자기장의 N극과 S극이 독립적으로 존재하는 자기홀극이 있을 수 없다는 것을 의미합니다. 반대로 말하면 자석은 N극와 S극이 항상 함께 존재함을 의미해요.
반면에 전기장의 발산은 0이 아닙니다. 그리고 전기장 선속도 0이 아니죠. 이것은 자석과 달리 전하는 양전하와 음전하가 독립적으로 존재할 수 있다는 것을 의미해요.
자기장은 전기장과는 다르다는 것을 알 수 있어요.





이 글 잘 읽었습니다. 벡터 미분 연산자와 발산 정리를 활용한 자기장 발산 구하는 과정이 매우 명확하게 설명되어 좋았습니다. 식 변환 과정도 순차적으로 표현되어 이해하기 쉬웠고, 특히 자기장의 발산이 0이 되는 부분이 핵심적이었습니다. 다만, 마지막 문단이 조금 더 구체적인 설명이 더 필요할 것 같기도 합니다.
방문해 주셔서 감사합니다. 그리고 마지막 문단의 내용은 나중에 다른 글에서 추가적으로 설명할 계획입니다. 의견 주셔서 고맙습니다.