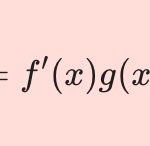제차 2계 선형 상미분 방정식 : 계수 낮추기(reduction of order)

BallPen · 2024-02-12T11:17:23+09:00

제차 2계 선형 상미분 방정식 해 중 하나를 알고 있을 때 1차 독립의 두번째 해를 구하는 방법입니다. 이 방법은 계수 낮추기(reduction of order) 방법으로써 이미 알고 해를 이용해 미분 방정식의 계수를 줄여 두번째 해를 구합니다.

Last Updated on 2024-02-12 by BallPen

제차 2계 선형 상미분 방정식의 한 해를 알 때 다른 해를 구하는 방법입니다.

제차 2계 선형 상미분 방정식 일반형은 다음과 같아요.

\tag{D1} y^{\prime \prime} + p(x) y^{\prime} + Q(x)y = 0

이 미분 방정식은 2계이므로 해가 2개 나와야 하는데요. 그중 하나의 해를 알고 있을 때 다른 해를 구하는 방법을 알아봐요.

결론부터 말씀드리면 하나의 해를 $y_1(x)$ 라고 할 때 다른 해 $y_2(x)$ 는 다음과 같이 주어집니다.

\tag{D1} \begin{align} y_2(x) = y_1 \int{{e^{-\int pdx}}\over{y_1^2}} dx \end{align}

이번 글에서는 위 (D1)식이 어떻게 도출되었는지 유도해 보고, 관련 예제도 풀어보겠습니다.

아래는 이번 글의 목차입니다.

Contents [hide]

1. 제차 선형 상미분 방정식 해의 특징
2. 제차 2계 선형 상미분 방정식 두번째 해
- 2-1. 첫번째 해
- 2-2. 1차 독립인 두번째 해
3. 제차 2계 선형 상미분 방정식 예제
- 3-1. 공식을 적용하지 않는 풀이
- 3-2. 공식을 적용하는 풀이

1. 제차 선형 상미분 방정식 해의 특징

제차 선형 상미분 방정식의 해는 두개의 특징을 갖는데요. 하나는 중첩의 원리(superposition principle)이고 다른 하나는 선형성(linearity)의 원리에요.

1-1. 중첩의 원리

두 함수 $y_1 (x)$ , $y_2 (x)$ 가 제차 선형 상미분 방정식 $F(x,y,y^{\prime}, y^{\prime\prime})=0$ 의 해이면 그 둘을 서로 합한 $y_1 (x)+ y_2 (x)$ 도 해입니다.

이것을 중첩의 원리라고 불러요.

1-2. 선형성의 원리

함수 $y_1 (x)$ 가 제차 선형 상미분 방정식 $F(x,y,y^{\prime}, y^{\prime\prime})=0$ 의 해이면 임의의 실수 $k$ 에 대해 $k y_1 (x)$ 도 해입니다.

이것을 선형성이라고 불러요.

1-3. 일차 결합과 1차 독립

중첩의 원리와 선형성의 원리에 따라 두 함수 $y_1 (x)$ , $y_2 (x)$ 가 제차 선형 상미분 방정식 $F(x,y,y^{\prime}, y^{\prime\prime})=0$ 의 해이면, 임의의 두 상수를 $c_1$ , $c_2$ 라 할 때 다음 식을 미분방정식의 일반해라고 합니다.

\tag{1-1} y = c_1 y_1 (x) + c_2 y_2 (x)

이러한 성질을 $y_1 (x)$ 와 $y_2 (x)$ 의 일차결합(linear combination)이라고 해요. 이때 $y_1 (x)$ 와 $y_2(x)$ 는 서로 1차 독립의 관계를 가져야 합니다.

만일 두 함수 $y_1 (x)$ 와 $y_2 (x)$ 가 적당한 상수 $c$ 에 대해 $y_2(x) = c y_1(x)$ 을 만족한다면 1차 종속이라고 해요. 그러나 이러한 상수 $c$ 가 존재하지 않으면 1차 독립(또는 선형 독립)이라고 합니다.

즉, 상수 $c_1$ , $c_2$ 에 대해 $c_1 y_1(x) + c_2 y_2(x)=0$ 을 만족하는 경우가 $c_1$ 과 $c_2$ 가 모두 0인 경우 밖에 없다면 두 함수는 1차 독립이 됩니다.

2. 제차 2계 선형 상미분 방정식 두번째 해

앞서 말씀드린것처럼 제차 2계 선형 상미분 방정식 일반형은 다음과 같아요.

\tag{2-1} y^{\prime \prime} + p(x) y^{\prime} + Q(x)y = 0

이 미분 방정식은 2계 미분방정식이므로 두 개의 해를 갖습니다. 그런데 그중 하나의 해를 이미 알고 있을 때 두번째 해를 구하는 방법을 설명드리는 것이 이번 글의 목적이에요.

2-1. 첫번째 해

첫번째 해는 이미 알고 있다고 가정해야 합니다. 이 상태에서 두번째 해를 어떻게 구하느냐 하는 것이니까요.

그래서 첫번째 해를 아래 (2-2)식처럼 정할께요.

\tag{2-2} y_1 (x)

자 이제부터 두번째 해 $y_2(x)$ 를 구해 봐요.

2-2. 1차 독립인 두번째 해

(2-1)식의 첫번째 해를 $y_1 (x)$ 로 정했으니 두번째 해의 모양을 정하면 좋겠는데요. 다음과 같이 일단 정해보겠습니다.

\tag{2-3} y_2 (x) = u(x) y_1(x)

그러면 제차 2계 선형 상미분방정식의 일반해는 (1-1)식에 따라 다음과 같이 쓸 수 있어요.

\tag{2-4} \begin{align} y &= c_1 y_1(x) + c_2 y_2(x)\\ &=c_1 y_1 (x) + c_2 u(x) y_1(x) \end{align}

이때 $u(x)$ 는 상수가 되면 안됩니다. 그 이유는 $y_1(x)$ 와 $y_2(x)$ 가 서로 1차 독립이어야 하기 때문이에요.

만일 $u(x)$ 가 상수 $u$ 가 된다면 $c_2 u$ 도 상수 $c$ 가 되므로 $y_2(x) = c y_1 (x)$ 의 관계가 성립합니다. 그러면 $y_2(x)$ 가 $y_1(x)$ 의 상수배로 주어지므로 1차 종속 관계가 성립하기 때문이에요.

한편, (2-3)식에 따라 우리가 구하고자 하는 $y_2(x)$ 에서 $y_1(x)$ 는 이미 알고 있으므로 $u(x)$ 만 구하면 된다는 것을 알 수 있어요.

이를 위해 (2-3)식에 주어진 해 $y_2(x)$ 를 한번 미분하고 또 한번 미분해봐요. 곱의 미분을 적용하면 됩니다. 그리고 식이 복잡하니 $x$ 의 함수임을 뜻하는 $(x)$ 의 기호를 이제부터 생략할게요.

\tag{2-5} \begin{align} &y^{\prime} = u^{\prime} y_1 + uy_1^{\prime}\\ &y^{\prime \prime} = u^{\prime \prime} y_1 + u^{\prime} y_1^{\prime }+u^{\prime} y_1^{\prime} + uy_1^{\prime\prime}\\ &~~~~=uy_1^{\prime \prime} + 2u^{\prime}y_1^{\prime} + u^{\prime\prime} y_1 \end{align}

이번에는 (2-5)식을 (2-1)식의 원래의 미분 방정식에 대입하세요.

\tag{2-6} \begin{align} &\Big( uy_1^{\prime \prime} + 2u^{\prime}y_1^{\prime} + u^{\prime\prime} y_1 \Big) + p\Big( u^{\prime} y_1 + uy_1 ^{\prime} \Big) + Q u y_1 = 0\\ \end{align}

그리고 윗식을 정리하면 다음과 같아요.

\tag{2-7} u\Big({\color{red}y_1^{\prime \prime} + p y_1^{\prime} + Qy_1} \Big) +{\color{blue} u^{\prime} \Big(2 y_1^{\prime} + p(x) y_1 \Big) + u^{\prime\prime} y_1 =0}

그런데 윗식에서 빨강색 부분은 원식인 (2-1)식에 의해 0이 됩니다. 그러므로 파랑색 부분만 더 정리해서 $u$ 를 구해봐요. 이를 위해 일단 $u^{\prime}$ 을 $w$ 로 치환하겠습니다.

그러면 아래와 같이 원식인 (2-1)식의 2계 선형 상미분방정식이 1계 선형 상미분방정식으로 계수가 낮아지게 됩니다. 그래서 이 풀이 방법을 계수 낮추기(reduction of order)라고 불러요.

\tag{2-8} \begin{align} &w\big(2 y_1^{\prime} + p y_1 \big) + w^{\prime}y_1 \\ &~~~~~~~~~=w\big(2 y_1^{\prime} + p y_1 \big) + {{dw}\over{dx}}y_1 =0 \end{align}

윗식의 두번째 줄에 대해 양변을 $\omega$ 로 나누고 ${{dx}\over{y_1}}$ 를 곱해주고 정리합니다.

\tag{2-9} \begin{align} {{dw}\over{w}} + 2{{y_1^{\prime}}\over{y_1}} dx + pdx =0\\[10pt] {{dw}\over{w}} + 2{{1}\over{y_1}}{{dy_1}\over{\cancel {dx}}} \cancel {dx} + pdx =0\\[10pt] {{dw}\over{w}} + 2{{dy_1}\over{y_1}} + pdx =0\\[10pt] \end{align}

이제 윗식 세번째 줄의 양변을 적분합니다.

\tag{2-10} \begin{align} &\int {{1}\over{\omega}}d \omega + \int 2 {{1}\over{y_1}}dy_1 + \int p dx = 0 \\ \end{align}

그러면 다음과 같아요.

\tag{2-11} \begin{align} &\ln|\omega| + \ln |y_1|^2 + \int pdx =0\\ &\ln|\omega y_1^2| = - \int p dx + c \end{align}

윗식의 양변에 exponential을 취하세요.

\tag{2-12} \begin{align} \omega y_1^2 &= \exp {\Big(-\int pdx + c\Big)}\\ &={\color{blue} \exp(c)}\exp \Big(-\int pdx\Big)\\ &={\color{blue}c_1}e^{-\int p dx} \end{align}

윗식에서 $e^{c}$ 는 상수이므로 $c_1$ 으로 나타냈어요. 그리고 아래와 같이 한번 더 정리합니다.

\tag{2-13} \begin{align} \omega = u^{\prime} = {{du}\over{dx}}&=c_1 {{e^{-\int pdx}}\over{y_1^2}}\\[5pt] du &= c_1 {{e^{-\int pdx}}\over{y_1^2}}dx\\ \end{align}

우리가 구하려고 하는 것은 $u$ 이므로 이번에는 윗식의 두번째 줄을 적분하세요.

\tag{2-14} u=c_1 \int{{e^{-\int pdx}}\over{y_1^2}} dx+c_2

이렇게 해서 우리가 구하려고 했던 $u(x)$ 를 구했습니다. (2-3)식에서 $y_2 (x) = u(x) y_1(x)$ 로 정했으므로 두번째 해인 $y_2(x)$ 를 구하면 다음과 같아요.

\tag{2-15} \begin{align} y_2(x) = c_1 y_1 \int{{e^{-\int pdx}}\over{y_1^2}} dx + \color {red}c_2y_1 \end{align}

이때 윗식의 빨강색은 일반해를 표현할 때 첫번째 해와 결합하게 됩니다(아래 예제 풀이 참고). 따라서 최종적으로 두번째 해는 다음과 같아요.

\tag{2-16} \begin{align} y_2(x) = y_1 \int{{e^{-\int pdx}}\over{y_1^2}} dx \end{align}

결국 (2-16)식을 이용하면 제차 2계 선형 상미분 방정식에서 하나의 해 $y_1(x)$ 를 알고 있을 때 두번째 해 $y_2(x)$ 를 구할 수 있게 됩니다.

3. 제차 2계 선형 상미분 방정식 예제

다음 미분방정식이 있습니다. 이 미분 방정식의 한 해를 $y_1 = x^2$ 으로 이미 알고 있을 때 두번째 해를 구해 보세요.

\tag{ex-1} x^2 y ^{\prime\prime} - 3xy^{\prime} + 5y =0

우선 위 식을 다음과 같이 정리해보니 제차 2계 선형 상미분 방정식 일반형의 모습이에요.

\tag{ex-2} y^{\prime\prime} - {3 \over x} y^{\prime} + {5 \over x^2} y =0

3-1. 공식을 적용하지 않는 풀이

두번째 해를 $y_2 = u y_1$ 로 가정합니다. 그리고 한번 미분하고, 두번 미분하여 정리하면 아래와 같습니다.

\tag{ex-3} \begin{align} &y_2 = u y_1\\ &y_2{^\prime} = u^{\prime} y_1 + uy_1^{\prime}\\ &y_2^{\prime\prime} = u^{\prime\prime} y_1 + 2 u^{\prime}y_1^{\prime} + u y_1^{\prime\prime} \end{align}

윗식을 원래 식인 (ex-1)식에 대입하고 다음과 같이 정리합니다.

\tag{ex-4} \begin{align} &x^2(u^{\prime\prime} y_1 + 2 u^{\prime}y_1^{\prime} + u y_1^{\prime\prime})-3x(u^{\prime} y_1 + uy_1^{\prime})+5uy_1 =0\\[5pt] &x^2y_1 u^{\prime\prime}+(2x^2 y_1^{\prime}-3xy_1)u^{\prime} + {\color{red}(x^2 y_1 ^{\prime\prime} - 3xy_1^{\prime} + 5y_1)}u=0 \end{align}

윗식에서 빨강색 부분은 원식과 같은 형태이므로 0이 됩니다.

한편 $y_1 = x^2$ , $y_1^{\prime}=2x$ , $y_1^{\prime\prime}=2$ 가 되므로 이 값들을 위 (ex-4)식의 두번째 줄에 대입하고 정리합니다.

\tag{ex-5} x^4 u^{\prime\prime} + x^3 u^{\prime} =0

그리고 $u^{\prime}$ 를 $\omega$ 로 치환합니다.

그러면 원식의 제차 2계 선형 상미분 방정식이 아래의 첫번째 줄과 같이 제차 1계 선형 상미분 방정식으로 계수가 낮아집니다. 정리해서 양변을 적분하세요.

\tag{ex-6} \begin{align} &x^4 {{d\omega}\over{dx}}+x^3 \omega =0\\[10pt] &{{dw}\over{\omega}} =-{{dx}\over{x}}\\[10pt] &\int{{dw}\over{\omega}} =-\int{{dx}\over{x}}\\[10pt] &\ln|\omega| = -\ln|x|+c\\[10pt] &\omega = c_1{1 \over x} \end{align}

윗식에서 $\omega$ 는 $u^{\prime}$ 이므로 이를 환원한 후 적분합니다.

\tag{ex-7} \begin{align} \omega = u^{\prime} = {{du}\over{dx}} = c_1{1 \over x} \end{align}

\tag{ex-8} \begin{align} u &=c_1 \int {1 \over x} dx\\ &=c_1 \ln|x|+c_2 \end{align}

따라서 두번째 해 $y_2$ 는 다음과 같습니다.

\tag{ex-9} \begin{align} y_2 = u y_1=(c_1 \ln|x|+c_2)x^2 \end{align}

결국 문제에 주어진 제차 2계 선형 상미분 방정식의 일반해는 다음과 같이 구해집니다.

\tag{ex-10} \begin{align} y &= c_3y_1 + c_4y_2\\ &=c_3x^2 + c_4 c_1x^2\ln|x|+c_4c_2 x^2\\ &=(c_3+c_4c_2)x^2 + c_4c_1 x^2\ln|x|\\ &=c_5x^2 + c_6x^2 \ln|x| \end{align}

3-2. 공식을 적용하는 풀이

제차 2계 선형 상미분 방정식 일반형으로 정리된 (ex-2)식을 참고하여 (2-16)식의 공식을 적용합니다.

\tag{ex-11} \begin{align} y_2 &= y_1 \int{{e^{-\int pdx}}\over{y_1^2}} dx\\[10pt] &=x^2\int{{e^{\int {3 \over x} dx}}\over{x^4}} dx\\[10pt] &=x^2 \int {{e^{\ln|x|^3}}\over{x^4}}dx \\[10pt] &=x^2 \int {1 \over x} dx\\[10pt] &=x^2 \ln |x| + \color{red}cx^2 \end{align}

이때 윗식에서 빨강색 부분은 일반해를 표현할 때 첫번째 해와 결합됩니다.

따라서 두번째 해 $y_2$ 는 다음과 같습니다.

\tag{ex-12} y_2 = x^2 \ln|x|

또한 두 해 $y_1(x)$ , $y_2(x)$ 에 대한 중첩의 원리와 선형성을 적용하면 일반해는 다음과 같습니다.

\tag{ex-13} \begin{align} y &= c_1 y_1 + c_2 y_2\\[10pt] &=c_1 x^2 + c_2 x^2 \ln|x| \end{align}

이 결과는 공식을 적용하지 않은 (ex-10)풀이 결과와 동일함을 알 수 있어요.

흥미롭고 도움이 되는 글이었나요? 리뷰를 부탁드립니다.

[Total: 1 Average: 5]

제차 2계 선형 상미분 방정식 : 계수 낮추기(reduction of order)