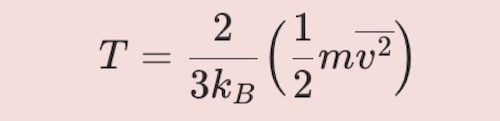Last Updated on 2025-12-16 by BallPen
기체 분자 운동론의 관점에서 기체의 온도를 생각해 봐요.
기체 분자 운동론에서의 온도 정의를 알아봐요.
결론부터 말씀드리면 기체 분자의 온도란 기체 분자의 평균 병진운동에너지와 직접적인 관련을 가져요. 따라서 기체의 온도가 높다라고 한다면 평균 병진 운동에너지의 크기가 크다는 뜻이에요.
1. 기체 분자 운동론에서의 압력
거시적 관점에서 압력 P는 단위면적 A당 작용하는 힘 F로서 다음과 같이 정의됩니다.
\tag{1}
\begin{align}
P= {F \over A}
\end{align}그런데 이 압력을 이상 기체에 대한 기체 분자의 운동 관점에서 미시적으로 설명할 수 있는데요.
기체 분자 운동론에서 압력은 단위부피 V당 분자 수 N과 분자의 평균 병진 운동에너지에 비례해요. 식으로 쓰면 다음과 같아요.
\tag{2}
\begin{align}
P = {2 \over 3} \Big( {N \over V} \Big) \Big( {1 \over 2} m \overline{v^2} \Big)
\end{align}2. 기체 분자 운동론에서의 온도
위 (2)식을 이용하면 기체의 온도를 분자의 운동 관점에서 설명할 수 있어요. 과연 기체의 온도는 분자의 운동에서 무엇에 대응할까요?
이를 알아보기 위해서는 우선 이상 기체 법칙에서 다음 관계가 성립하는 것을 상기해야 합니다.
\tag{3}
\begin{align}
PV = N k_B T
\end{align}여기서 k_B는 볼츠만상수(Boltzmann’s constant)이며 k_B = 1.38 \times 10^{-23} ~\rm{J/K}입니다. 그리고 T가 바로 온도에요.
그러면 (2)식을 (3)식의 형태로 최대한 대응시켜 보세요. 그러면 다음과 같아요.
\tag{4}
\begin{align}
PV = N k_B {\color {blue}{2 \over {3k_B}} \Big( {1 \over 2} m \overline{v^2} \Big) }
\end{align}이때 위 식에서 파랑색 수식 부분이 바로 온도 T에 대응하는 것을 알 수 있어요.
\tag{5}
\begin{align}
T= {2 \over {3k_B}} \Big( {1 \over 2} m \overline{v^2} \Big)
\end{align}즉, 기체의 온도는 분자의 평균 병진 운동에너지와 관련되어 있어요.
그래서 온도가 높으면 분자의 평균 병진운동에너지가 크고, (2)식에서처럼 용기의 부피와 기체의 양이 일정하다면 압력이 증가함을 이해할 수 있어요.