소리 세기 공식의 유도

BallPen · 2023-02-26T10:24:43+09:00

소리 세기 공식을 유도하여 압력 진폭 최대값과의 관계를 알아봅니다. 소리 세기란 단위 면적당 단위 시간당 전달되는 에너지의 평균값입니다. 이 관계를 도출한 후 적절히 수식을 변형하면 소리의 세기는 압력 진폭 최대값의 제곱에 비례함을 알 수 있습니다.

Last Updated on 2023-03-07 by BallPen

소리 세기 공식을 유도하여, 소리 세기와 압력 진폭과의 관계를 알아봅니다.

소리 세기 (sound intensity, wave intensity, 음파 세기) 공식은 데시벨(dB)을 이용한 소음도 측정이나 소리와 관련된 물리 현상을 해석하는데 자주 사용됩니다.

특히 소리 세기와 소리의 압력 진폭 사이의 관계식이 유용하게 사용됩니다.

함께 알아봐요.

아래는 이번 글의 목차입니다.

Contents

1. 기본 개념
- 1-1. 유체속 소리의 속력
- 1-2. 소리의 변위와 압력
2. 소리 세기 공식 유도
3. 소리 세기 – 압력진폭 관계

1. 기본 개념

소리 세기 공식을 유도하기 위해서는 몇가지 기본 개념을 정리하는 것이 필요합니다.

1-1. 유체속 소리의 속력

공기와 같은 유체는 압력이 작용하면 그 유체의 부피가 변하게 됩니다. 예를 들어 압력이 증가하면 공기의 부피는 감소하고 압력이 감소하면 부피는 증가하죠.

이와 같이 압력이 계기압력(gauge pressure) $\Delta p$ 만큼 변할 때 유체의 부피 변형 $\Delta V / V_0$ 의 비율을 부피 탄성율(bulk modulus)이라고 부릅니다. 여기서 $V_0$ 는 원래의 부피입니다.

\tag{1} B={{부피~변형력}\over{부피~ 변형}} = -{{\Delta p}\over{\Delta V / V_0 }}

(1)식에서 분자의 압력변화량 $\Delta p$ 를 부피변형력이라는 용어로 사용했는데요. 그 이유는 압력이 단위면적당 작용하는 힘으로 부피 변형을 일으키는 원인이 되기 때문입니다.

또한 (1)식에서 음의 부호는 부피 탄성율을 항상 양의 값으로 만들기 위해 부여되었습니다. 즉 압력이 증가하여 $\Delta p$ 가 양의 값을 가지면 물체의 부피가 감소하여 $\Delta V$ 가 음의 부호를 갖게 됩니다. 그래서 공식에 처음부터 음의 부호를 붙여줌으로써 $B$ 를 양수로 만드는 것이죠.

한편 유체의 밀도를 $\sigma$ 라고 한다면 유체를 통과하는 음파의 전달 속력 $v$ 는 다음과 같이 유도됩니다.

\tag{2} v = \sqrt{B \over \sigma}

따라서 공기나 물과 같은 유체속을 통과하는 파동의 속력은 부피탄성율과 밀도에만 의존합니다.

1-2. 소리의 변위와 압력

[소리의 변위]

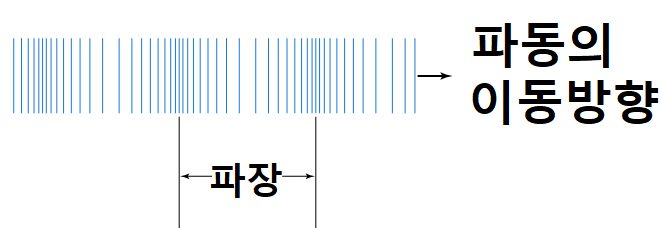
소리는 매질의 진동방향과 파동의 진행방향이 평행한 종파입니다. 따라서 소리가 만드는 파동, 즉 음파는 어느 순간 $t$ 에서 [그림 1]과 같이 공기분자의 변위에 따라 밀한 부분과 소한 부분으로 구분할 수 있죠.

[그림 1] 음파는 종파로써 밀한 부분과 소한 부분으로 구성됩니다. (그림 인용: 위키백과)

밀한 부분은 상대적으로 공기분자의 이동 변위가 작아 분자들이 모여있고, 소한 부분은 공기분자의 변위가 커 분자들이 멀리 흩어져 있을 것입니다. 이러한 상태에서 $+x$ 방향으로 소리가 전파해 갈 때 변위 $y$ 를 수학적으로 나타내면 다음과 같습니다.

\tag{3} y(x,t) = A \cos (kx - \omega t)

(3)식에서 종속변수인 변위를 $y$ 로 표기했습니다만 그 변위의 방향은 $x$ 방향이 됩니다. 왜냐면 위에서 말씀드렸듯이 음파는 종파이기 때문에 매질의 변위 방향과 파동의 진행방향이 평행하기 때문이에요.

단지 편의를 위해서 마치 종파를 횡파처럼 표현한 식으로 보시면 됩니다.

(3)식에서 $A$ 는 변위의 최대값이고, $k$ 는 파수(wave number)라고 부르며 $2 \pi /\lambda$ , $\omega$ 는 각진동수라고 부르며 $\omega = 2 \pi f = 2 \pi f \lambda / \lambda = vk$ 의 관계를 갖습니다.

[소리의 압력]

소리가 만드는 음파는 밀한 부분과 소한 부분으로 구분되고 이러한 파동이 공간상을 전파해 나갑니다.

그렇다면 왜 밀한 부분과 소한 부분으로 공기의 밀도가 변하게 될까요? 그 이유는 바로 음파가 공간상의 압력변화를 만들어내기 때문입니다.

따라서 압력이 작은 부분은 팽창하여 공기의 밀도가 작아지고, 압력이 큰 부분은 수축하여 공기의 밀도가 증가합니다. 이러한 방식으로 밀하고 소한 부분이 만들어지는 것을 상상하면 좋아요.

아래 [그림 2]는 어느 순간 $t$ 에서 (3)식으로 주어지는 음파의 변위를 나타낸 것입니다. 횡파처럼 그려져 있습니다만 엄밀하게는 매질의 진동방향이 파동의 진행방향과 평행한 종파임을 계속 기억해야 합니다.

그림을 보면 $x$ 와 $x+\Delta x$ 인 지점에서 각각의 공기분자의 변위가 $y_1$ 과 $y_2$ 임을 나타내고 있습니다.

이것을 공간 부피 변화 관계로 이해하며 다음과 같습니다.

[그림 3]에 단면적이 $S$ 인 음영이 있는 원기둥이 그려져 있습니다. 이 원기둥은 음파의 파동이 없을 때 공간상에 있는 공기의 부피를 의미해요.

그런데 음파의 파동이 이 공간을 지나게 되면 [그림 2]에 따라 원기둥의 왼쪽 끝인 $x$ 지점은 $y_1 = y(x,t)$ 만큼 변위되어 그림에서 보라색 원으로 표시된 부분까지 이동합니다.

동일한 방식으로 음영이 있는 원기둥의 오른쪽 끝인 $x+\Delta x$ 지점은 $y_2 = y(x+\Delta x,t)$ 만큼 변위되어 그림에서 가장 오른쪽에 보라색 원으로 표시된 부분까지 이동합니다.

결국 음영이 있는 원기둥의 원래 부피가 공기분자의 변위에 의해 보라색 원들 사이의 부피로 팽창한 것을 상상할 수 있을거에요. 이와 같이 공기의 부피가 팽창한다는 것은 압력의 변화가 있다는 것을 의미합니다.

이 압력의 변화를 수식으로 나타내 보겠습니다.

[소리의 압력 공식 유도]

소리가 만드는 압력 변화 $\Delta p$ 을 유도하기 위해서는 (1)식의 부피탄성율 공식을 사용합니다. 부피탄성율 $B$ 를 알고 있다면 $\Delta V / V_0$ 만 구하면 됩니다.

[그림 3]에서 원기둥의 부피 변화는 다음과 같습니다.

\tag{4} \begin{align} \Delta V &= {나중부피 - 처음부피}\\ &= S\Big( (\Delta x + y_2) - y_1 \Big) - S(\Delta x)\\ &= \cancel {S \Delta x} + S(y_2 - y_1) -\cancel{S(\Delta x)}\\ &=S(y_2 - y_1) \end{align}

(4)식을 변수관계를 보이기 위해 구체적으로 다시 쓰면 아래와 같습니다.

\tag{5} \Delta V = S\big[y(x+\Delta x, t) - y(x,t) \big]

만일 $\Delta x$ 가 0으로 가는 극한을 생각하고, (5)식을 원래의 부피 $V_0$ 로 나누면 다음과 같습니다.

\tag{6} {dV \over V_0} = \lim _{\Delta x \rightarrow 0} {{S\big[y(x+\Delta x, t) - y(x,t) \big]}\over{S \Delta x}}={{\partial y (x,t)}\over{\partial x}}

이제 (6)식을 (1)식에 대입하고 위치 $x$ 와 시간 $t$ 에서의 압력 $\Delta p(x,t)$ 는 아래와 같이 쓸 수 있어요.

\tag{7} \Delta p (x,t) = - B {{\partial y (x,t)}\over{\partial x}}

그러므로 (3)식에 주어진 변위 $y(x,t)$ 를 (7)식에 대입하고 정리하면 아래와 같습니다.

\tag{8} \begin{align} \Delta p (x,t) &= -B {{\partial}\over{\partial x}} (A \cos (kx - \omega t))\\ &= BkA \sin (kx - \omega t) \end{align}

(8)식에서 $BkA$ 는 상수들 끼리의 곱으로써 최대값을 나타내므로 이를 $\Delta p _{max}$ 로 치환하여 다시 쓰면 아래와 같습니다.

\tag{9} \Delta p (x, t) = \Delta p _{max} \sin(kx-\omega t)

바로 (9)식이 음파의 압력진폭 변화를 나타내는 식이 되겠습니다.

(3)식의 변위식과 (9)식의 압력식을 비교할 때 서로 간에 위상이 직각으로 어긋납니다. 즉 변위가 작은 밀한 곳이 압력이 높고, 변위가 큰 소한 곳이 압력이 낮다는 의미입니다.

2. 소리 세기 공식 유도

모든 파동은 한 공간에서 다른 공간으로 에너지를 전파합니다. 이때 단위 면적당, 단위시간당 전달되는 에너지를 파동의 세기(wave intensity)라고 하죠.

소리 세기, 즉 파동 세기의 단위는 $\mathrm{W/m^2}$ 입니다.

소리 세기를 수학적으로 표현하면 다음 (10)식과 같습니다. 이때 일률 $P$ 는 $P={E/t} = {F \cdot s/t} = F\cdot v$ 의 관계를 적용합니다. 또한 압력 $\Delta p$ 는 단위면적당 작용하는 힘으로써 $\Delta p=F/A$ 의 관계가 성립합니다.

\tag{10} I = {{E}\over{A \cdot t}} = {P \over A} = {{F \cdot v}\over{A}} = \Delta p\cdot v

(10)식을 적용하여 소리 세기 $I$ 를 구하기 위해서는 소리의 속력 $v$ 를 구한 후 (9)식에 유도한 $\Delta p$ 와 곱하면 됩니다.

우선 $v$ 는 (3)식의 변위식을 시간으로 미분하면 구할 수 있습니다.

\tag{11} v(x,t) = {{\partial y(x,t)}\over{\partial t}} = {{\partial}\over{\partial t}}(A \cos (kx - \omega t))=\omega A \sin(kx-\omega t)

결국,

\tag{12} \begin{align} I(x,t) &= \Delta p(x,t) \cdot v(x,t)\\ & = BkA \sin (kx - \omega t) \cdot \omega A \sin(kx-\omega t)\\ &=b\omega k A^2 \sin^2 (kx-\omega t) \end{align}

이 됩니다. 그런데 (12)식에 따르면 소리 세기는 싸인의 제곱 형태로 주어집니다. 이를 그래프로 그리면 아래 [그림 4]와 같습니다.

[그림 4] 소리 세기 곡선은 시간에 따라 일정하지 않습니다. 그래서 평균을 내면 하나의 대표 값으로 만들 수 있어요.

[그림 4]에서 빨강색으로 그려진 소리 세기 곡선은 일정하지 않습니다. 이 말은 소리가 전달하는 파동 에너지가 어느 순간에는 전달되었다가 어느 순간에는 0이 되는 현상이 반복된다는 말이죠.

에너지가 전달이 되기는 하는데 그것이 시간에 따라 변합니다. 이러한 경우 소리 세기의 평균을 사용한다면 하나의 대표적인 값으로 나타낼 수 있을거에요.

다시 말해 (12)식으로 주어진 함수의 평균값을 구하는 거에요. 평균 낼때 상수의 평균은 상수 그 자신이 될 뿐이에요. 그래서 사인 제곱 함수 부분만 평균을 내면 됩니다.

\tag{13} \bar I = b\omega k A^2 \overline{ \sin^2 (kx-\omega t)}

싸인 제곱 함수의 평균을 구하는 방법은 여기를 참고하세요. 결과적으로 그 값은 1/2이 나온답니다.

최종적으로, 소리 세기의 평균값은 다음과 같습니다.

\tag{14} \bar I = {1 \over 2} b \omega kA^2

여기에 (3)식에서 설명드린 $\omega = vk$ , (2)식의 $v^2 = B / \sigma$ 를 대입하면 아래와 같이 쓸 수 도 있습니다.

\tag{15} \begin{align} \bar I &= {1 \over 2} B \omega k A^2\\ &= {1 \over 2} B v k^2 A^2\\ &={1 \over 2} B \sqrt{{B}\over {\sigma}}k^2 A^2\\ &={1 \over 2} \sigma v^2 \sqrt{{B}\over{\sigma}}k^2 A^2\\ &={1 \over 2} \sqrt{\sigma B} v^2 k^2 A^2\\ &={1 \over 2} \sqrt{\sigma B} \omega^2 A^2 \end{align}

3. 소리 세기 – 압력진폭 관계

소리 세기 $\bar I$ 와 압력 진폭의 최대값 $\Delta p_{max}$ 사이의 관계를 유도하기 위해서는 $\omega = vk$ , (9)식의 $\Delta p_{max} = BkA$ 의 관계를 사용합니다.

이 관계들을 (15)식에 대입하고 정리해보면 다음과 같습니다.

\tag{16} \begin{align} \bar I &= {1 \over 2} \sqrt{\sigma B}\omega^2 A^2\\ &={1 \over 2} \sqrt{\sigma B} v^2 \cancel {k^2} {{\Delta p_{max}^2}\over{B^2 \cancel{k^2}}}\\ &={1 \over 2} \sqrt{\sigma B} {B \over \sigma} {{\Delta p_{max}^2}\over{B^2}}\\ &={1 \over 2} {{\Delta p_{max}^2}\over{\sqrt{\sigma B}}}\\ &={1 \over 2} {{\Delta p_{max}^2}\over{\sqrt{\sigma \sigma v^2}}}\\ &={{\Delta p_{max}^2}\over{2 \sigma v}} \end{align}

지금까지 소리 세기 공식을 유도한 후, 소리 세기 $\bar I$ 와 압력진폭의 최대값 $\Delta p_{max}$ 사이의 관계를 알아보았습니다.

위 내용과 연계하여 소음크기 데시벨 (dB)까지 알아보고 싶은 사람은 여기를 클릭하세요.

흥미롭고 도움이 되는 글이었나요? 리뷰를 부탁드립니다.

[Total: 7 Average: 3.9]

소리 세기 공식의 유도