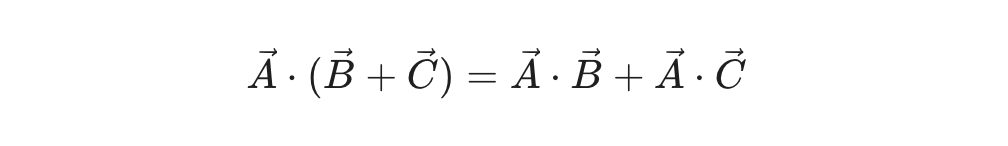Last Updated on 2023-12-04 by BallPen
내적 즉, 스칼라곱의 분배법칙 성립에 대한 증명입니다.
내적의 분배법칙 증명을 이번 글에서 다룹니다.
내적이 궁금한 분은 이전 글을 참조해 주세요.
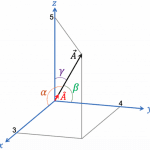
다음 세 개의 벡터가 있습니다.
\tag{1}
\vec A = A_x \hat{x} + A_y \hat{y} + A_z \hat{z}\tag{2}
\vec B = B_x \hat{x} + B_y \hat{y} + B_z \hat{z}\tag{3}
\vec C = C_x \hat{x} + C_y \hat{y} + C_z \hat{z}이 벡터들에 대해 \vec{A} \cdot ( \vec{B} + \vec{C} )를 구해 보겠습니다.
\tag{4}
\begin{align}
\vec{A} \cdot ( \vec{B} + \vec{C} ) &= \vec{A} \cdot \Big[(B_x + C_x)\hat{x} + (B_y + C_y)\hat{y} + (B_z + C_z) \hat{z} \Big]\\
&=(A_x \hat{x} + A_y \hat{y} + A_z \hat{z}) \cdot \\
&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\Big[(B_x + C_x)\hat{x} + (B_y + C_y)\hat{y} + (B_z + C_z) \hat{z} \Big]\\
&=A_x (B_x + C_x) + A_y(B_y + C_y) + A_z (B_z + C_z)\\
&=A_x B_x + A_x C_x + A_y B_y + A_y C_y + A_z B_z + A_z C_z\\
&=(A_x B_x + A_y B_y + A_z B_z) + (A_x C_x + A_y C_y + A_z C_z)\\
&=\vec{A} \cdot \vec{B} + \vec{A}\cdot \vec{C}
\end{align}결과적으로 다음 (5)식으로 주어지는 내적의 분배 법칙이 성립함을 알 수 있습니다.
\tag{5}
\vec A \cdot (\vec B + \vec C) = \vec A \cdot \vec B + \vec A \cdot \vec C흥미롭고 도움이 되는 글이었나요? 리뷰를 부탁드립니다.
[Total: 5 Average: 4]
1 thought on “내적의 분배법칙”