Last Updated on 2025-09-01 by BallPen
열역학적 과정 중 단열 과정에 대한 이야기입니다.
단열 과정 (adiabatic process)은 지난 글에서 설명드린 등적 과정, 등온 과정과 함께 열역학적 과정 중의 하나입니다. 물론 등압 과정도 있어요.
지난 글에 이어 이번 글에서도 기체의 분자 운동을 고려하여 단열 과정을 이해해 봐요.
시작하겠습니다. 아래는 이번 글의 목차입니다.
Contents
1. 열역학 주요 개념 복습
아래의 내용은 계로 유입된 열량 Q, 내부에너지 변화량 \Delta U, 계가 한 일 W, 계 내의 압력 P에 대한 주요 개념입니다.
만일 아래의 내용이 잘 이해가 안가시면 이전 글을 먼저 보고 오시면 좋습니다.
첫째, 열량 Q는 뜨거운 물체에서 차가운 물체로 전달되는 에너지입니다.
둘째, 내부에너지 U의 크기는 계 내에 있는 기체 분자의 온도 T에 비례하며, 기체분자의 온도는 기체분자가 갖는 운동에너지 KE에 비례합니다. 결국 기체분자가 상대적으로 빠르게 움직이면 운동에너지가 크고, 기체 분자의 온도가 높으며, 내부에너지도 큽니다.
\tag{1}
\color{blue}U \propto T \propto KE따라서 내부에너지 변화량 \Delta U는 다음의 관계를 갖습니다.
\tag{2}
\color{blue}\Delta U \propto \Delta T \propto \Delta KE즉 온도가 변한만큼, 운동에너지가 변한만큼에 비례해서 내부에너지 변화량이 결정됩니다.
셋째, 계가 한 일 W는 계의 부피가 변화한 량 \Delta V에 비례합니다. 만일 계의 부피가 변하지 않으면 계가 한 일은 0입니다. 압력이 일정할 때 계가 한 일의 공식은 아래 (3)식과 같습니다.
\tag{3}
\color{blue}W = P \Delta V넷째, 계 내부의 압력 P는 단위부피 V당 기체분자의 운동에너지 KE를 뜻합니다. 따라서 다음의 관계가 성립합니다.
\tag{4}
\color{blue}P \propto {T \over V} \propto {KE \over V}2. 단열 과정
단열 과정은 기체 분자가 들어 있는 계가 외부와 어떠한 열적 교환도 하지 않는 열역학적 과정을 말합니다. 이와 달리 등적 과정과 등온 과정에서는 계로 열량 Q가 유입되거나 유출되는 경우를 다루죠.
이와 같이 계가 외부와 열적으로 고립되었을 때 우리는 단열되었다라고 표현합니다. 예를 들어 겨울철 바깥의 차가운 공기가 집안으로 들어오지 못하도록 단열재를 잘 사용하잖아요. 바로 그 단열재가 실내를 외부와 단열하기 위해 사용되는 것입니다.
그래서 이 열역학적 과정을 단열 과정이라 부릅니다.
단열 과정이 일어나는 동안의 기체 분자 운동, 열역학 제1법칙, PV 도표가 어떻게 달라지는지 순서대로 알아보겠습니다.
2-1. 단열 과정에서의 분자 운동
아래 [그림 1]에는 실린더가 하나 있습니다. 이 실린더의 모든 벽은 외부와 열적으로 단열되어 열량 Q의 유입이나 유출이 전혀 없다고 생각해 보세요.
다만, 실린더 위쪽에 있는 피스톤은 실린더 내의 기체 분자와 충돌하여 밀려 올라갈 수 있어요. 이것을 단열 팽창이라고 합니다. 반대로 무엇인가가 피스톤을 아래쪽으로 밀어 내린다면 기체를 압축하게 되잖아요. 그것을 단열 압축이라고 해요.
이번 글에서는 단열 팽창만 고려하겠습니다. 단열 압축은 단열 팽창의 반대 개념을 상상하시면 쉽게 이해하실 수 있어요.
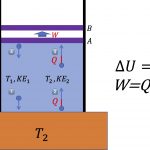
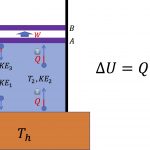
![[그림 1] 단열 과정. 실린더 내에 온도 <span class="katex-eq" data-katex-display="false">T_1</span>의 기체분자가 들어있으며, 외부와는 열적으로 단열되어 있습니다. 다만 실린더 위쪽에 있는 피스톤은 기체분자의 충돌에 의해 밀려 올라갈 수 있습니다.](https://ballpen.blog/wp-content/uploads/2022/07/Picture1-2-1024x675.jpg)
[그림 1]에는 기체 분자 4개가 그려져 있어요. 그 중 \textcircled{1}번의 기체분자는 T_1의 온도와 그에 대응하는 운동에너지 KE1을 갖고 있어요.
이 기체분자는 아래쪽 벽과 충돌하지만 아래쪽 벽은 단단히 고정되어 있고 탄성충돌을 가정하므로 온도와 운동에너지의 크기는 동일하게 유지되고 운동 방향만 바뀌게 됩니다.
충돌 후의 기체 분자를 표현한 것이 \textcircled{2}번 분자에요.
\textcircled{2}번 분자는 \textcircled{1}번 분자와 운동 방향만 바뀌었고 화살표의 길이인 운동에너지의 크기와 온도도 동일하게 유지되고 있어요.
\textcircled{2}번 분자는 계속 이동하여 그림의 \textcircled{3}번 분자처럼 실린더의 피스톤과 충돌하게 됩니다.
그런데 이 피스톤은 실린더의 다른 벽들과는 다르게 기체 분자와의 충돌에 의해 밀려 올라갈 수 있어요. 물론 수많은 기체분자들이 피스톤과 충돌하여 밀려 올라가는 것을 상상해야 합니다.
이에 따라 \textcircled{3}번 분자가 피스톤과 충돌하여 일을 하게 되고 그 결과 피스톤이 최초 위치 A위치에서 B위치로 움직이게 됩니다.
결국 기체가 들어있는 원통형 실린더의 내부 부피가 늘어나게 되어 팽창하게 되는 것이죠.
그렇다면 기체 분자가 피스톤과 충돌하면서 피스톤을 밀어 올렸다면 충돌 후의 기체 분자는 어떻게 될까요?
바로 [그림 1]의 \textcircled{4}번 분자처럼 바뀌게 됩니다.
\textcircled{3}번 분자와 비교하여 충돌에 의해 운동 방향이 바뀌었고요. 그 다음에는 화살표의 길이에 대응하는 운동에너지의 크기가 작아진 것을 알 수 있어요. 이것은 (1)식에 따라 분자의 온도가 낮아진 것과 같아요.
이와 같이 실린더 내에 있는 기체 분자들은 무작위 운동을 하는 도중에 피스톤과 여러번 충돌을 경험하게 됩니다.
그때마다 피스톤은 위쪽으로 조금씩 밀려 올라가게 되고 분자의 운동에너지, 즉 분자의 온도는 계속 낮아집니다. 결국 (2)식과 같이 운동에너지가 감소하여 분자 온도가 감소하고, 이것은 기체 분자의 내부에너지가 감소한다는 것을 뜻해요.
결국 나중 내부에너지에서 처음 내부에너지를 빼면 내부에너지의 변화량은 음수가 된다는 것을 꼭 기억하세요.
2-2. 단열 과정에서의 열역학 제1법칙
열역학 제1법칙은 에너지보존법칙으로서 \Delta U = Q-W입니다.
단열 과정은 외부와 계(실린더) 사이의 열적 교환이 일어나지 않는 것을 가정하므로 Q=0이 성립합니다.
이에 따라 열역학 제1법칙은 다음과 같이 표현될 수 있어요.
\tag{5}
\Delta U = -W이번에는 단열 과정에서의 내부에너지 변화량인 \Delta U를 생각해봐요.
[그림 1]에서 설명한 것처럼 단열 팽창과정에서 기체 분자들은 피스톤과 계속 충돌하여 피스톤을 밀어내는 일 W를 하게 됩니다. 이 과정에서 기체 분자의 운동에너지가 작아지고 온도는 내려가며 내부에너지도 감소하게 된다고 설명드렸습니다.
그래서 단열 팽창이 일어나는 동안 나중 내부에너지에서 처음 내부에너지를 뺀 내부에너지 변화량 \Delta U는 위에서 말씀드린 대로 음수값을 갖게 됩니다.
물론 반대로 단열 압축이 일어나도록 피스톤에 일 -W를 해준다면, 하강되는 피스톤과 기체분자가 충돌하여 기체분자의 운동에너지, 온도, 내부에너지가 증가하게 됩니다.
하강하는 피스톤과 충돌한 기체 분자는 충돌 전에 비해 속도가 더욱 빨라져 운동에너지가 증가하기 때문이에요. 그러므로 이 경우 \Delta U는 양의 값을 갖게 됩니다.
2-3. 단열 과정에서의 PV 도표
이전 글에서 설명드린 것처럼 PV 도표(또는 PV 다이어그램)로 계의 압력, 부피, 온도의 상태변수를 하나의 점으로 표현할 수 있어요.
아래 [그림 2]는 단열 과정 동안 PV 도표가 어떻게 변하는지를 보여주고 있습니다.
![[그림 2] 단열 과정에 대한 PV 도표. <span class="katex-eq" data-katex-display="false">A</span>점이 <span class="katex-eq" data-katex-display="false">B</span>점으로 이동하는 것이 단열과정입니다. 이때 <span class="katex-eq" data-katex-display="false">T_2 < T_1</span>입니다.](https://ballpen.blog/wp-content/uploads/2022/07/Picture7-1024x841.jpg)
[그림 2]와 같이 단열 과정은 마치 등온 과정과 유사하게 변합니다. 차이가 있다면 등온 과정은 등온선을 따라 경로가 변하여 계의 온도가 일정하게 유지되지만 단열 과정은 경로가 더욱 가파르게 변하여 계의 온도가 달라진다는 것입니다.
[그림 2] 처럼 단열 팽창하는 동안 계의 온도가 T_1에서 T_2로 하강하게 되요.
이것은 [그림 1]에서 설명했던 것처럼 피스톤과 기체분자가 충돌하여 기체분자의 온도가 내려가는 것과 같은 이치입니다.
또한 단열 팽창이 일어나는 동안 실린더 내부의 부피가 팽창하는 것을 [그림 2]에서 확인할 수 있어요. 즉 부피가 V_A에서 V_B로 커지는 것을 알 수 있습니다.
이것은 \Delta V가 어느 값을 갖게 되므로 한 일 W가 존재함을 뜻합니다.
압력은 어떻게 될까요?
압력은 (4)식에서 설명한것처럼 단위부피당 운동에너지(또는 온도)로 정의됩니다. 그런데 단열 팽창이 일어나는 동안 분자의 운동에너지는 점점 감소하고 계의 부피는 점점 증가합니다.
그러므로 단열 팽창이 일어나는 동안 압력은 당연히 감소하게 됩니다. [그림 2]의 PV 도표에서 P_A의 압력이 P_B로 낮아지는 것을 알 수 있어요.
3. 단열 과정에서 한 일의 크기
앞서 설명드린 것처럼 단열 팽창에서는 계의 부피가 점점 증가하게 되어 계가 외부로 일을 하게 됩니다.
그렇다면 한 일의 크기는 어떻게 구할 수 있을까요? 함께 알아보겠습니다.
개념적으로는 계가 한 일의 크기는 [그림 2]에서 A점과 B점을 잇는 경로 아래쪽의 면적에 대응합니다.
그 면적을 구하기 전에 단열 과정에서 압력과 부피의 관계를 우선 고민해볼 필요가 있습니다.
3-1. 단열 과정에서 압력과 부피의 관계
열역학 제1법칙은 아래와 같이 주어지죠.
\tag{6}
\Delta U = Q-W이때 단열과정이므로 Q=0입니다.
내부에너지의 미소변화량 dU는 nC_v dT로 주어집니다. 여기서 n은 기체의 몰수이고, C_v는 등적몰비열(molar specific heat at constant volume)이라고 합니다.
일의 미소변화량 dW는 (3)식과 같이 pdV가 되겠습니다. 이를 종합하여 (6)식을 다시쓰면 아래와 같습니다.
\tag{7}
\begin{aligned}
dU &=-dW\\[8pt]
nC_v \textrm{d}T &= -P \textrm{d}V\\
\end{aligned}한편 이상기체상태방정식 PV=nRT를 임의의 x로 미분하면 다음의 관계가 성립합니다.
\tag{8}
\begin{aligned}
{d(PV) \over dx} &= nR{dT \over dx}\\[8pt]
P{dV \over dx} + V{dP \over dx} &= nR{dT \over dx}\\[8pt]
PdV + VdP &=nRdT
\end{aligned}또한 (8)식의 가장 마지막 줄을 dT로 정리하면 다음과 같게 되죠.
\tag{9}
dT={1 \over nR}\big(PdV + VdP)이번에는 (9)식을 (7)식의 두번째 줄에 대입하고 정리해 보세요.
\tag{10}
\begin{aligned}
nC_v dT &= -PdV\\[8pt]
nC_v {1 \over nR} \big( PdV + VdP \big)&=-PdV\\[8pt]
C_v V dP + C_v PdV &= -RPdV\\[8pt]
C_v VdP + (C_v + R)PdV &= 0
\end{aligned}(10)식의 가장 마지막 줄에서 C_v + R은 정압몰비열 C_p에 해당합니다. 또한 양변을 C_v PV로 나누면 다음과 같습니다.
\tag{11}
\begin{align}
{1 \over P}dP + {C_p \over C_v} {1 \over V} dV = 0
\end{align}여기서 C_p / C_v는 열용량의 비율로서 상수이므로 \gamma로 치환한 후에 적분해 봐요. 한편 C_p는 C_v보다 크므로 \gamma는 1보다 큰 값을 갖습니다.
\tag{12}
\begin{aligned}
\int{1 \over P}dP + \gamma\int{1 \over V}dV &= 0\\[8pt]
\ln P + \gamma \ln V &= C\\[8pt]
\ln P + \gamma \ln V &= \ln k\\[8pt]
\ln{P}{V}^\gamma &= \ln k\\[8pt]
PV^\gamma &= k=일정
\end{aligned}위 식에서 C는 적분상수입니다. 이 적분상수가 어떤 일정한 값 k에 로그를 취한 값과 동일한 것으로 간주했어요.
한편, 이상기체상태방정식에 따르면 PV/T도 일정하잖아요. (12)식의 가장 마지막에 P=T / V를 대입해 보세요. 그러면 아래의 관계도 성립해요.
\tag{13}
\begin{aligned}
PV^\gamma &= 일정\\[8pt]
{T \over V} V^{\gamma} &= 일정\\[8pt]
TV^{\gamma -1} &= 일정
\end{aligned}3-2. 단열 과정에서 한 일
이제 (12)식의 가장 마지막 줄에서 P=kV^{-\gamma}의 관계를 이용해 단열 과정에서 계가 한 일을 구해보겠습니다.
\tag{14}
\begin{aligned}
W &= \int_{V_A}^{V_B} PdV\\[8pt]
&=\int_{V_A}^{V_B} kV^{-\gamma} dV\\[8pt]
&=k\Big[ {{V^{-\gamma +1}}\over{-\gamma+1}} \Big]_{V_A}^{V_B}\\[8pt]
&={k \over {1-\gamma}}\Big({V_B}^{1-\gamma} - {V_A}^{1-\gamma} \Big)
\end{aligned}한편 (12)식의 마지막 줄을 다음과 같이 구체적으로 쓸 수 있습니다.
\tag{15}
\begin{align}
P_A {V_A}^{\gamma} = P_B {V_B}^{\gamma} = k
\end{align}그리고 위 (15)식을 (14)식에 대입하여 식을 변형하면 다음의 관계도 성립합니다.
\tag{16}
\begin{aligned}
W&={k \over {1-\gamma}}\Big({V_B}^{1-\gamma} - {V_A}^{1-\gamma} \Big) \\[8pt]
&={1 \over{1-\gamma}}\big( P_B {V_B}^{\gamma} {V_B}^{1-\gamma} - P_A {V_A}^{\gamma} {V_A}^{1-\gamma} \big)\\[8pt]
&={1 \over {1-\gamma}}\big(P_BV_B - P_A V_A \big)
\end{aligned}지금까지 단열 과정에 대해 말씀 드렸습니다. 다음 글에서는 정압 과정에 대해 설명드리겠습니다.