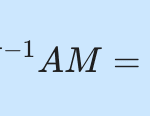Last Updated on 2024-01-06 by BallPen
완전미분방정식이 아닌 불완전미분방정식을 어떻게 푸는지 알아봐요.
불완전미분방정식(Non-exact differential equation)이란 완전미분방정식은 아니지만 특별한 방법을 써서 완전미분방정식처럼 문제를 풀수 있는 미분방정식을 말합니다.
우선 간단한 예제부터 시작하면 아주 재미있게 그 풀이 원리를 이해할 수 있어요.
참고로 미분방정식에 대한 글을 계속 올리고 있어요. 이와 관련된 다양한 글들을 보고 싶으면 화면 위쪽의 검색창에 ‘미분방정식’을 입력해 보세요.
그럼 이제부터 시작합니다.
아래는 이번 글의 목차입니다.
Contents
1. 미분방정식 예제
1-1. 완전미분방정식이 아닌 방정식(불완전미분방정식)
불완전미분방정식의 풀이법을 공부하기 전에 우선 다음의 미분방정식을 완전미분방정식 풀이법으로 풀어보세요. 혹시 완전미분방정식 풀이법이 잘 기억이 나지 않으면 이전 글을 참고하기 바랍니다.
\tag{1}
\bold{-ydx + x dy =0}완전미분방정식 풀이법을 적용하기 위해서는 (1)식에서 -y를 M(x,y)로, x를 N(x,y)로 치환합니다.
그리고 아래의 관계가 성립하면 완전미분방정식 풀이법을 적용할 수 있어요.
\tag{2}
{\partial M(x,y) \over {\partial y}} = {\partial N(x,y) \over {\partial x}}(2)식의 관계가 성립하는지 적용해봐요.
\tag{3}
\begin{align}
&{\partial M(x,y) \over{\partial y}} = {\partial (-y) \over {\partial y}} = -1\\
&{\partial N(x,y) \over {\partial x}} = {\partial x \over {\partial x}} = 1\\
\end{align}그 결과 -1과 1이 도출되어 같지 않습니다. 결국 (2)식의 관계가 성립하지 않으므로 주어진 미분방정식은 완전미분방정식 풀이법을 적용할 수 없습니다. 이러한 경우의 미분방정식을 불완전미분방정식이라고 해요.
2-2. 불완전미분방정식 변형
그런데 만일 (1)식의 좌변과 우변에 1/x^2을 곱하면 어떻게 될까요? 좌변과 우변에 같은 양을 곱했으므로 수학적으로 (1)식이 달라지는 것은 전혀 없어요.
예를 들어 x+2y=0의 좌변과 우변에 2를 곱하면 2x + 4 y =0이 됩니다. 이것을 정리하면 2(x+2y) =0로 쓸 수 있으며, 이 관계가 성립하기 위해서는 x+2y =0가 되어야 하므로 2를 곱하기 전과 동일한 관계가 유지되고 있음을 알 수 있어요.
결국 같은 수를 방정식의 좌변과 우변에 곱해주더라도 아무 상관없어요.
그런데 (1)식의 좌변과 우변에 하필 1/x^2을 곱한다고 하는데 그 이유는 나중에 이해하실 수 있어요. 일단 1/x^2이 어떻게 도출되었는지는 나중에 알아보고 일단 곱해봐요.
그러면 (1)식은 다음과 같이 변형됩니다.
\tag{4}
\begin{align}
{1 \over x^2 }\times(-ydx + x dy) &= {1 \over x^2}\times0\\
{- {y \over x^2}} dx+ {1 \over x}dy &= 0
\end{align}
그리고 (4)식이 (2)식의 완전미분방정식 조건을 만족하는 지의 여부를 아래 (5)식으로 확인해 보겠습니다.
\tag{5}
\begin{align}
&{\partial M(x,y) \over{\partial y}} = {\partial (-y/x^2) \over {\partial y}} = -{1 \over x^2}\\
&{\partial N(x,y) \over {\partial x}} = {\partial (1/x) \over {\partial x}} = - {1 \over x^2}\\
\end{align}신기하게도 동일한 값이 도출되어 (2)식이 성립하고 있음을 알 수 있습니다. 이것은 (4)식이 완전미분방정식이며 통상적인 완전미분방정식 풀이법을 적용할 수 있음을 뜻해요.
그리고 (4)식을 풀어 도출된 일반해는 (1)식에 주어진 미분방정식의 일반해와 같습니다.
(4)식을 완전미분방정식으로 풀이하는 방법은 여기를 참고하세요. 또한 (1)식은 완전미분방정식이 아닌 변수분리형 미분방정식 풀이법으로도 해를 구할 수 있습니다. 그 풀이과정도 여기를 클릭하세요.
(4)식과 (1)식을 만족하는 일반해는 다음 (6)식과 같습니다. 여기서 c는 상수입니다.
\tag{6}
x = cy지금까지 어느 불완전미분방정식에 어떤 함수를 곱함으로써 완전미분방정식으로 식을 변형할 수 있고, 이를 통해 일반해를 구하는 예시를 말씀드렸어요.
지금까지 오셨으면 아마도 불완전미분방정식에 어떤 함수를 곱해야 완전미분방정식이 될 수 있느냐가 궁금할 거에요. 이제부터 그 이야기를 시작합니다.
2. 적분인자 유도
식 (4)에서 불완전미분방정식에 1/x^2을 곱해주었더니 완전미분방정식으로 바뀌었어요. 일단 완전미분방정식으로 식이 변형되면 정해진 풀이법을 적용해 일반해를 구할 수 있습니다.
이때 불완전미분방정식에 곱하는 어떤 특별한 함수를 ‘적분인자(integrating factor)’라고 부릅니다. ‘적분’ 단어가 들어가 있으니 적분의 형태로 주어지는 어떠한 함수를 말해요.
그렇다면 이제부터 적분인자를 구하는 방법을 알아보겠습니다. 이 방법만 알면 불완전미분방정식일지라도 완전미분방정식으로 변형하여 문제를 풀수 있게 돼요.
아래 (7)식은 불완전미분방정식이라고 생각해 보세요. 즉 {{\partial M(x,y)}\over{\partial y}} \ne {{\partial N(x,y)}\over{\partial x}} 가 성립해요.
\tag{7}
M(x,y) dx + N(x,y)dy =0이 불완전미분방정식에 어떤 x와 y의 함수로 주어진 적분인자 F(x,y)를 곱해서 완전미분방정식으로 변형할 수 있다고 가정해봐요.
그러면 아래와 같이 표현할 수 있습니다.
\tag{8}
M(x,y)F(x,y) dx + N(x,y)F(x,y)dy =0그리고 (8)식은 조금 복잡하니 M(x,y)F(x,y)를 M_1 (x,y)로 치환하고, N(x,y)F(x,y)를 N_1 (x,y)로 치환해 봐요.
\tag{9}
M_1 (x,y) dx + N_1 (x,y)dy =0아주 간단해 졌어요.
그런데 위에서 가정한 것처럼 불완전미분방정식인 (7)식에 적분인자를 곱해서 (9)식은 완전미분방정식이 되었어요. 그러면 (9)식은 다음의 관계를 만족해야만 합니다.
\tag{10}
{{\partial M_1 (x,y)}\over{\partial y}} = {{\partial N_1 (x,y)}\over{\partial x}}그리고 곱의 미분 공식 {{d(uv)}\over{dx}} = {{du}\over{dx}}v+u{{dv}\over{dx}}을 적용하면 아래와 같습니다.
\tag{11}
\begin{align}
&{{\partial M(x,y)}\over{\partial y}}F(x,y)+ M(x,y){{\partial F(x,y)}\over{\partial y}} \\
&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~= {{\partial N(x,y)}\over{\partial x}}F(x,y)+ N(x,y){{\partial F(x,y)}\over{\partial x}}
\end{align}복잡해 보이는 식이 나왔어요. 이 (11)식을 잘 정리해서 적분인자 F(x,y)를 구할 수 있으면 좋겠는데요. 아쉽게도 너무 복잡해서 그리 쉬워보이지 않아요.
그래서 한번 더 가정을 합니다. (11)식을 조금 더 간단한 형태로 바꾸면 좋겠어요.
이를 위해 적분인자가 x만의 함수로 되어 있거나 y만의 함수로 되어 있다고 가정해봐요.
그럼 하나씩 알아봐요.
2-1. 적분인자가 x만의 함수인 경우
만일 적분인자가 x만의 함수 F(x)로 주어진다면, (11)식은 다음과 같이 표현됩니다.
\tag{12}
\begin{align}
&{{\partial M(x,y)}\over{\partial y}}F(x)+ \color {red}M(x,y){{\partial F(x)}\over{\partial y}} \color{black}\\
&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~= {{\partial N(x,y)}\over{\partial x}}F(x)+ \color{blue} N(x,y){{dF(x)}\over{\ dx}}
\end{align}이때 빨강색 항은 x만의 함수인 적분인자 F(x)를 y로 편미분하므로 0이 됩니다.
또한 파랑색 항은 x만의 함수를 x로 미분하므로 상미분으로 표현을 바꿀 수 있어요.
계속 정리해 봐요.
\tag{13}
{{\partial M(x,y)}\over{\partial y}}F(x)= {{\partial N(x,y)}\over{\partial x}}F(x)+ N(x,y){{dF(x)}\over{dx}}\tag{14}
\Big({{\partial M(x,y)}\over{\partial y}}- {{\partial N(x,y)}\over{\partial x}}\Big)F(x)= N(x,y){{dF(x)}\over{dx}}\tag{15}
{{1}\over{F(x)}}{{dF(x)}\over{dx}}= {{1}\over{N(x,y)}} \Big({{\partial M(x,y)}\over{\partial y}}- {{\partial N(x,y)}\over{\partial x}}\Big)\tag{16}
{{1}\over{F(x)}}dF(x)= {{1}\over{N(x,y)}} \Big({{\partial M(x,y)}\over{\partial y}}- {{\partial N(x,y)}\over{\partial x}}\Big)dx(16)식의 양변을 적분해보세요. 이때 \int {1 \over x} dx = \ln |x| + c의 관계를 활용합니다. 적분상수 c는 임의의 상수이므로 0으로 간주해도 좋습니다.
\tag{17}
\ln |F(x)|= \int{{1}\over{N(x,y)}} \Big({{\partial M(x,y)}\over{\partial y}}- {{\partial N(x,y)}\over{\partial x}}\Big)dx로그의 성질 e^{\ln |x|} = x을 활용하기 위해 양변에 exponential을 취해 줍니다.
\tag{18}
\bold{F(x)= e^{\int{{1}\over{N(x,y)}} \Big({{\partial M(x,y)}\over{\partial y}}- {{\partial N(x,y)}\over{\partial x}}\Big)dx}}최종적으로 구한 (18)식이 적분인자 F(x)를 구하는 공식이 됩니다. 이 적분인자를 불완전미분방정식에 곱하면 완전미분방정식으로 바뀌게 됩니다.
이번에는 y만의 함수 F(y)로 주어지는 적분상수도 구해봐요.
2-2. 적분인자가 y만의 함수인 경우
적분인자가 y만의 함수 F(y)로 주어진다면, (11)식은 다음과 같이 표현됩니다.
\tag{19}
\begin{align}
&{{\partial M(x,y)}\over{\partial y}}F(y)+ \color {blue}M(x,y){{d F(y)}\over{dy}} \color{black}\\
&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~= {{\partial N(x,y)}\over{\partial x}}F(y)+ \color{red} N(x,y){{\partial F(y)}\over{\partial x}}
\end{align}이때 파랑색 항은 y만의 함수를 y로 미분하므로 상미분으로 바꾸었어요. 빨강색 항은 y만의 함수를 x로 편미분하므로 0이됩니다.
그러면 다음과 같이 정리할 수 있어요.
\tag{20}
{{\partial M(x,y)}\over{\partial y}}F(y)+ \color {black}M(x,y){{d F(y)}\over{dy}} \color{black}= {{\partial N(x,y)}\over{\partial x}}F(y)\tag{21}
\Big({{\partial N(x,y)}\over{\partial x}} -{{\partial M(x,y)}\over{\partial y}} \Big)F(y)= \color {black}M(x,y){{d F(y)}\over{dy}} \color{black}\tag{22}
\begin{align}
{{1}\over{F(y)}}{{d F(y)}\over{dy}} \color{black} = {{1}\over{M(x,y)}}\Big({{\partial N(x,y)}\over{\partial x}} -{{\partial M(x,y)}\over{\partial y}} \Big)
\end{align}\tag{23}
\begin{align}
{{1}\over{F(y)}}dF(y) \color{black} = {{1}\over{M(x,y)}}\Big({{\partial N(x,y)}\over{\partial x}} -{{\partial M(x,y)}\over{\partial y}} \Big) dy
\end{align}(23)식의 양변을 적분해 보세요.
\tag{24}
\begin{align}
\ln |F(y)| = \int{{1}\over{M(x,y)}}\Big({{\partial N(x,y)}\over{\partial x}} -{{\partial M(x,y)}\over{\partial y}} \Big) dy
\end{align}양변에 exponential을 취합니다.
\tag{25}
\begin{align}
\bold{F(y) = e^{\int{{1}\over{M(x,y)}}\Big({{\partial N(x,y)}\over{\partial x}} -{{\partial M(x,y)}\over{\partial y}} \Big) dy}}
\end{align}(25)식이 적분인자 F(y)입니다. 이 적분인자를 불완전미분방정식에 곱하면 완전미분방정식으로 바뀌게 됩니다.
지금까지 적분인자를 구하는 방법을 알아봤습니다. 적분인자만 구하면 불완전미분방정식이 완전미분방정식으로 바뀌게 되므로 완전미분방정식 풀이법을 적용하여 일반해를 구합니다.
이쯤되면 이해하셨을 거에요. (1)식에 1/x^2을 곱하여 불완전미분방정식을 완전미분방정식으로 바꾸었는데, 그때 1/x^2 이 바로 적분인자 F(x)에 해당합니다.
관련 예제를 함께 풀어보겠습니다.
3. 불완전미분방정식 풀이 예제
다음 미분방정식의 일반해를 구해보세요.
\tag{q-1}
\bold{2ydx + 3xdy=0}문제에 주어진 식이 완전미분방정식인지의 여부를 알아봐요.
식의 2y를 M(x,y)로, 3x를 N(x,y)로 생각하고 (2)식의 관계가 성립하는지를 확인해 봅니다.
\tag{q-2}
\begin{align}
&{\partial M(x,y) \over {\partial y}} = {{\partial (2y)}\over{\partial y}} = 2\\
&{\partial N(x,y) \over {\partial x}} = {{\partial (3x)}\over{\partial x}} = 3
\end{align}그 결과 두 값이 서로 달라 (2)식의 관계가 성립하지 않아요. 이 말은 문제에 주어진 식이 완전미분방정식이 아니라는 뜻입니다.
그럼 이번에는 적분인자를 구한 후, 적분인자를 문제의 양변에 곱하여 완전미분방정식으로 바꾸어 볼까요? 그러면 문제를 풀 수 있을 거에요.
적분인자를 구해 봅니다.
3-1. 적분인자가 x만의 함수인 경우
(18)식을 적용해봐요.
\tag{q-3}
\begin{align}
F(x) &= \exp\Big[{\int{{1}\over{N(x,y)}} \Big({{\partial M(x,y)}\over{\partial y}}- {{\partial N(x,y)}\over{\partial x}}\Big)dx} \Big]\\
&=\exp\Big[\int {1 \over{3x}}\Big( {{\partial (2y)}\over{\partial y}}-{{\partial (3x)}\over{\partial x}} \Big) dx\Big]\\
&=\exp \Big[ \int{{1}\over{3x}}\big(2-3\big)dx \Big]\\
&=\exp \Big[-{{1}\over{3}}\int{1 \over x}dx \Big]\\
&=\exp\Big[-{{1}\over{3}}\ln |x| + c_1 \Big]\\
&=\exp(c_1)\exp\Big( -{1 \over 3} \ln|x|\Big)\\
&=c_2 e^{(-1/3) \ln |x|}\\
&=c_2 e^{\ln |x|^{-1/3}}\\
&=c_2 x^{-1/3}
\end{align}(q-3)식을 전개하는 과정에서 상수 곱하기 상수는 또 하나의 상수로 간주될 뿐입니다. 또한 상수에 exponential 취해도 상수가 됩니다. 풀이를 단순화하기 위해서 (q-3)식의 가장 마지막 줄에 있는 상수 c_2를 1로 두겠습니다. 그리고 구해진 적분상수를 문제의 양변에 곱해줍니다.
그러면 다음과 같아요.
\tag{q-4}
(x^{-1/3}) 2ydx + (x^{-1/3})3xdy=0\tag{q-5}
\begin{align}
2(x^{-1/3}) ydx + 3(x^{2/3})dy=0
\end{align}그렇다면 (q-5)식이 완전미분방정식이 되었을까요? 그럼 확인해봐요.
\tag{q-6}
\begin{align}
&{\partial M(x,y) \over{\partial y}} = {\partial (2x^{-1/3}y) \over {\partial y}} = 2x^{-1/3}\\
&{\partial N(x,y) \over {\partial x}} = {\partial (3x^{2/3}) \over {\partial x}} = 2x^{-1/3}\\
\end{align}(q-6)식과 같이 두 값이 서로 같다는 것을 알 수 있습니다. 결국 (q-5)식은 완전미분방정식이 되었어요.
그러면 (q-5)식을 완전미분방정식 풀이법을 적용하여 일반해를 구하면 됩니다.
그 일반해는 다음과 같아요.
\tag{q-7}
y=cx^{-2/3}이렇게 해서 적분인자가 x만의 함수로 주어질 때 미분방정식의 일반해를 구했어요. 이쯤되면 아마도 적분인자가 y만의 함수로 주어진 경우에는 어떻게 되나 하고 궁금할 거에요.
그것도 한번 구해 봐요.
3-2. 적분인자가 y만의 함수인 경우
이번에는 (25)식을 적용합니다.
\tag{q-8}
\begin{align}
F(y) &= \exp \Big[{\int{{1}\over{M(x,y)}}\Big({{\partial N(x,y)}\over{\partial x}} -{{\partial M(x,y)}\over{\partial y}} \Big) dy}\Big]\\
&=\exp\Big[\int{{1}\over{2y}} \Big({{\partial(3x)}\over{\partial x}} - {{\partial(2y)}\over{\partial y}} \Big) dy \Big]\\
&=\exp\Big[\int{{1}\over{2y}}(3-2)dy \Big]\\
&=\exp\Big[{1 \over 2}\int{1 \over y} dy \Big]\\
&=\exp\Big[{1 \over 2} \ln |y| + c_1 \Big]\\
&=\exp(c_1) \exp\Big({1\over 2} \ln |y| \Big)\\
&=c_2 e^{(1/2) \ln|y|}\\
&=c_2 e^{\ln|y|^{1/2}}\\
&=c_2 y^{1/2}
\end{align}여기서도 풀이를 단순화하기 위해 상수 c_2는 1로 두겠습니다. 그리고 (q-8)의 적분상수를 문제의 양변에 곱합니다.
\tag{q-9}
(y^{1/2}) 2ydx + (y^{1/2})3xdy=0\tag{q-10}
\begin{align}
2(y^{3/2}) dx + 3x(y^{1/2})dy=0
\end{align}(q-10)도 완전미분방정식이 되었는지 확인해보겠습니다.
\tag{q-11}
\begin{align}
&{\partial M(x,y) \over{\partial y}} = {\partial (2y^{3/2}) \over {\partial y}} = 3y^{1/2}\\
&{\partial N(x,y) \over {\partial x}} = {\partial (3xy^{1/2}) \over {\partial x}} = 3y^{1/2}\\
\end{align}두 값이 동일하게 나왔으니 (q-10)은 완전미분방정식이 맞습니다. 이제는 완전미분방정식 풀이법을 적용하여 풀면 됩니다.
그리고 그 일반해를 구해보면 다음과 같아요.
\tag{q-12}
y=cx^{-2/3}그 결과 (q-7)식과 동일한 결과가 얻어집니다. 적분인자를 F(x)로 구하든 F(y)로 구하든 미분방정식의 일반해는 동일하게 주어집니다.
이상으로 불완전미분방정식 풀이 방법을 설명드렸습니다.
2 thoughts on “불완전미분방정식 풀이 방법”