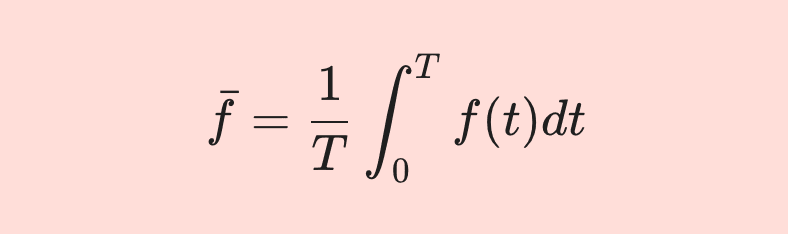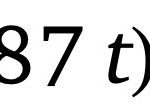Last Updated on 2024-01-06 by BallPen
사인 제곱 함수의 평균값 계산을 해보겠습니다.
함수의 평균값은 교류신호의 평균값이나 파동의 세기 등을 계산할 때 많이 사용됩니다.
예를 들어 주기적으로 반복되는 주기 함수 f(t)의 평균값 \bar f(t)은 다음의 공식으로 구할 수 있습니다.
\tag{1}
\bar f = {1 \over T} \int _0^Tf(t)dt(1)식에서 T는 함수의 주기값입니다.
[예제]
예제를 하나 풀어보죠. 다음 사인 제곱 함수의 평균값을 구해보세요.
\tag{2}
f(t) = \sin^2 t이 함수의 평균값은 (1)식을 적용하여 구하면 됩니다. 이때 주기 T는 -\pi에서 \pi까지 2 \pi 주기로 설정하겠습니다.
\tag{3}
\begin{align}
\bar f(t) &= {1 \over T} \int_0^T f(t) dt\\
&={1 \over 2\pi} \int_{-\pi}^{\pi} \sin^2{t}dt\\
\end{align}한편 두배각 공식에 따르면 \sin^2{x} = {{1-\cos{(2x)}}\over{2}}가 됩니다. 이를 (3)식에 대입하고 계속 풀어나갑니다.
\tag{4}
\begin{align}
\bar f(t) &= {1 \over 2\pi} \int_{-\pi}^{\pi} \sin^2{t}dt\\
&={1 \over 2\pi} \int_{-\pi}^{\pi}{{1-\cos(2t)}\over{2}} dt\\
&={1 \over {2 \pi}}\times{1 \over 2} \int_{- \pi}^{\pi} 1- \cos(2t) dt\\
&={1 \over {4 \pi}} \Big(\int_{-\pi}^{\pi} 1dt - \int_{-\pi}^{\pi}\cos(2t)dt\Big)\\
&={1 \over {4 \pi}} \Big( \big[t\big]_{-\pi}^{\pi} - \big[{1 \over 2}\sin(2t)\big]_{-\pi}^{\pi}\Big)\\
&={1 \over{4 \pi}} \Big((\pi - (-\pi))-{1 \over 2}\big(\sin(2 \pi) - \sin(-2 \pi)\big) \Big)\\
&={1 \over {4 \pi}}\Big(2 \pi - {1 \over 2}(0) \Big)\\
&={1 \over {4 \cancel \pi}} 2 \cancel\pi\\
&={1 \over 2}
\end{align}결과적으로 사인 제곱 함수의 평균값은 1/2입니다.
참고로 주기가 같고 초기 위상만 다른 코사인 제곱 함수의 평균값도 동일하게 1/2이 나온다는 것을 꼭 기억하세요.
\tag{5}
\bar f(t) = {1 \over 2\pi} \int_{-\pi}^{\pi} \cos^2{t}dt = {1 \over 2}흥미롭고 도움이 되는 글이었나요? 리뷰를 부탁드립니다.
[Total: 3 Average: 5]
1 thought on “사인 제곱 함수의 평균값”