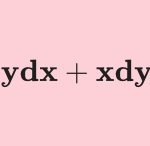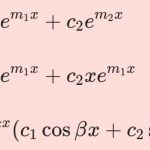상미분방정식 풀이 | WolframAlpha

Last Updated on 2024-03-17 by BallPen

울프람 알파로 상미분방정식의 일반해와 특수해를 구하는 방법입니다.

상미분방정식 문제를 WolframAlpha로 풀어 볼게요.

물론 간단한 미분방정식은 손으로 직접 풀어보는 것이 제일 좋아요. 하지만 미분방정식이 복잡하거나 손으로 푼 결과가 맞는지 확인하고 싶을 때는 WolframAlpha를 사용하는 것도 좋은 방법이라고 생각해요.

상미분방정식 예시를 들고 일반해와 특수해를 구해 보겠습니다.

아래는 이번 글의 목차에요.

1. 상미분방정식 예제

다음의 이계 선형 상미분방정식의 일반해를 WolframAlpha로 구해 보세요. 여기서 x는 변위이고, t는 시간이라고 하겠습니다.

\tag{1}
{{d^2x}\over{dt^2}} + 0.2 {dx \over dt} + x =0

1-1. 일반해

(SOL) 문제에 주어진 상미분방정식을 푼다는 것은 시간의 함수로서의 변위 x(t)를 구한다는 의미입니다.

상미분방정식을 WolframAlpha에 입력할 때는 아래와 같이 미분기호 ‘프라임’을 사용하면 됩니다. 이때 x가 t의 함수임을 알려주기 위해 x(t) 형태로 입력해 주세요.

x(t)'' + 0.2x(t)'+x(t) = 0

그 결과 WolframAlpha가 구해준 일반해는 다음과 같습니다.

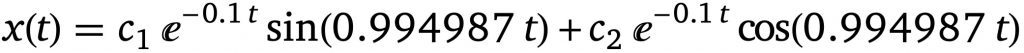
여기서 c_1과 c_2는 초기 조건으로 결정되는 상수에요. 이 상수들까지 모두 구하면 그것을 특수해라고 불러요.

1-2. 특수해

위에서 구한 일반해에 초기 조건을 적용하면 특수해를 구할 수 있어요.

초기조건은 말 그대로 초기의 조건인데요. 미지수가 c_1과 c_2 두개이므로 초기조건도 두개가 있어야 해요.

보통은 x(t)에서 t=0일 때의 초기 변위, 그리고 변위를 시간으로 미분한 x^{\prime}(t)에서 t=0일 때의 초기 속도를 초기조건으로 사용합니다. 그리고 이 과정에서 얻어진 두 식을 연립해서 풀면 c_1과 c_2를 구할 수 있어요.

그런데 WolframAlpha를 이용하면 초기조건을 처음부터 지정해줄 수 있어요. 그러면 특수해를 아주 쉽게 구해줍니다.

아래의 입력식이 그 예시인데요.

x(0)=1은 변위 x(t)에 t=0을 대입했을 때 초기 변위가 1이라는 초기조건입니다. 또한 x^{\prime}(0)=0은 x(t)를 시간 t로 미분한 x^{\prime}(t)에 t=0을 대입했을 때의 초기 속도값이 0이라는 초기조건이에요.

이 상황은, 용수철에 매달린 물체를 예로 든다면 물체를 밀어 용수철을 1 cm 만큼 압축한 상태에서 손으로 잡고 있다가 t=0인 순간에 손에서 물체를 놓은 상황하고 같아요. 그래서 초기 위치 x(0)=1이고, 초기 속도 x^{\prime}(0)=0이 되는 거죠.

WolframAlpha에 아래의 입력식을 복사해서 붙여넣기 해보세요.

x(t)'' + 0.2x(t)'+x(t) = 0, x(0)=1, x'(0)=0

그 결과 특수해는 다음과 같습니다.

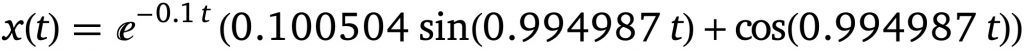
일반해와 비교할 때 c_1은 0.100504이고, c_2는 1이라는 것을 알 수 있어요.

1-3. 특수해의 그래프

위에서 특수해를 구했으니 WolframAlpha로 그래프를 그려볼까요. 이때 가로축의 범위는 0~100까지, 세로축은 -1.2~1.2까지 그리도록 설정해봐요.

이를 위해서는 아래 식처럼 ‘plot’ 명령어를 사용하면 됩니다.

이때 그래프의 가로축이 시간 t이고 세로축이 변위 x가 되어야 하잖아요. 그런데 수식에 t가 들어가 있으니 가로축은 WolframAlpha가 시간으로 잘 그려주지만 세로축은 기본값이 y로 되어 있다는 것을 유념하세요. 그래서 출력범위 설정할 때 x가 아닌 y의 범위를 지정해주어야 합니다.

plot(e^(-0.1 t) (0.100504 sin(0.994987 t) + cos(0.994987 t))) t=0 to 100, y=-1.2 to 1.2

결과 그래프는 다음과 같아요.

가로축과 세로축의 출력 범위가 설정한대로 잘 그려졌어요.

Related posts.

다문화 신혼부부 출신 국적. 미국 남편, 중국 아내가 2위, 그럼 1위는? 강력범죄 피해자는 무엇을 하고 있었을까? 2위는 취침중, 그럼 1위는? 청소년 알레르기 비염 – 청소년 10명중 3명 이상이 진단 받아 로그 기본 성질과 로그 활용 사례 미분방정식 예제1 : -ydx + xdy =0 cos 2pi/3 값 구하기 벡터 화살표 그리기 | WolframAlpha 제차 이계 상미분 방정식 : 상수 계수