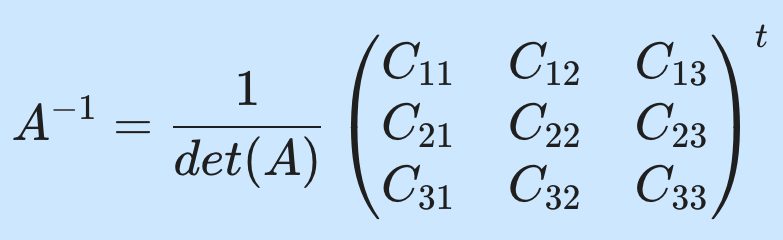Last Updated on 2024-08-18 by BallPen
역행렬이 어떻게 정의되고, 또 그 성질은 어떤지 알아봐요.
역행렬(inverse matrix)이란 어떤 정방행렬에 곱했을 때 단위행렬을 만들어내는 행렬을 말합니다.
즉, 행과 열이 같은 어떤 정방행렬 A가 있을 때 이 정방행렬의 앞 또는 뒤에 A의 역행렬 A^{-1}을 곱해주면 단위 행렬 I가 만들어져요.
AA^{-1} = I~~~~~~or~~~~~~A^{-1}A = I그러면 역행렬 A^{-1}은 어떻게 만들 수 있을까요? 결론부터 말씀드리면 다음과 같아요.
A^{-1} = {{1}\over{det(A)}}
\begin{pmatrix}
C_{11} & C_{12} & C_{13}\\
C_{21} & C_{22} & C_{23}\\
C_{31} & C_{32} & C_{33}
\end{pmatrix}^{t}여기서 det(A)는 행렬 A의 행렬식, C_{ij}는 행렬 a_{ij} 원소에 대응하는 여인수(cofactor)입니다. 그리고 윗첨자 t는 전치행렬을 뜻합니다.
그럼 이제부터 윗 식들이 어떻게 도출되었으며, 그 역행렬의 주요 성질을 알아봐요.
아래는 이번 글의 목차입니다.
Contents
1. 행렬식과 여인수 복습
행과 열이 같은 정방행렬을 생각해봐요. 예를 들어 3×3 행렬 A가 있을 때 그 행렬식 det(A)는 다음과 같습니다.
\tag{1-1}
\begin{align}
det(A) &=
\begin{vmatrix}
a_{11} & a_{12} & a_{13}\\
a_{21} & a_{22} & a_{23}\\
a_{31} & a_{32} & a_{33}
\end{vmatrix}\\[10pt]
&=(a_{11} a_{22} a_{33} - a_{11} a_{32} a_{23})\\
&~~~~~~~~~~~~~~~~+(a_{12}a_{23}a_{31}-a_{12}a_{21}a_{a33}) \\
&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~+ (a_{13}a_{32} a_{21}-a_{13}a_{22}a_{31})
\end{align}
한편 여인수란 행렬의 한 원소가 속한 행과 열을 제외한 부분의 소행렬식(minor)에 규칙에 따라 부호를 붙인 것을 말해요. 그리고 행렬의 한 행(또는 열)에 대한 원소와 그 여인수를 서로 곱한 후 모두 합한 것을 여인수 전개라고 하죠.
이때 여인수 전개 결과는 행렬식과 같아요.
어떤 행렬 원소 a_{ij}에 대응하는 여인수 C_{ij}는 다음 식으로 구합니다.
\tag{1-2}
C_{ij} = (-1)^{i+j} M_{ij}여기서 (-1)^{i+j}는 여인수의 부호를 결정하고, M_{ij}는 원래의 행렬에서 i행과 j열을 제외한 부분의 소행렬식을 뜻합니다.
예를 들어 (1-1)식의 3×3 행렬에서 첫번째 행에 대한 여인수 전개 는 다음과 같죠.
\tag{1-3}
\begin{align}
det(A) &=
\begin{vmatrix}
a_{11} & a_{12} & a_{13}\\
a_{21} & a_{22} & a_{23}\\
a_{31} & a_{32} & a_{33}
\end{vmatrix}\\[10pt]
&=a_{11} C_{11} + a_{12}C_{12} + a_{13} C_{13}\\[10pt]
&=a_{11}(-1)^{1+1} M_{11} + a_{12}(-1)^{1+2}M_{12} + a_{13}(-1)^{1+3}M_{13}\\[10pt]
&=a_{11}M_{11} - a_{12}M_{12}+a_{13}M_{13}
\end{align}2. 역행렬
어떤 수에 그 역수를 곱하면 1이 됩니다. 예를 들어 숫자 3에 3의 역수를 곱하면 단위 숫자 1이 되죠. 이를 식으로 쓰면 다음과 같습니다.
\tag{2-1}
3 \times 3^{-1} = 3 \times {1 \over 3} = 1그러면 어떤 수에 역수를 곱하면 1이 되는 관계를 행렬연산에도 확대해서 적용해봐요. 즉, 어떤 행렬에 그 행렬의 역행렬을 곱해주면 단위행렬(unit matrix) I가 된다고 생각해 보자는 거에요. 식으로 표현하면 다음과 같아요. 이때 I는 항등행렬(identity matrix)이라고도 불러요.
\tag{2-2}
A A^{-1} = I예를 들어 아래에 행렬 A가 있어요. 이제부터 이 행렬의 역행렬 A^{-1}을 구해봐요.
\tag{2-3}
A=
\begin{pmatrix}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{pmatrix}우선 행렬 A의 각 원소에 대응하는 여인수 행렬을 만들고 이를 전치한 행렬을 B행렬이라고 정의할 게요.
\tag{2-4}
B=
\begin{pmatrix}
C_{11} & C_{12} & C_{13}\\
C_{21} & C_{22} & C_{23}\\
C_{31} & C_{32} & C_{33}
\end{pmatrix}^{t}
=
\begin{pmatrix}
C_{11} & C_{21} & C_{31} \\
C_{12} & C_{22} & C_{32} \\
C_{13} & C_{23} & C_{33}
\end{pmatrix}그리고 A행렬과 B행렬을 곱한 결과를 다음과 같이 표현하겠습니다.
\tag{2-5}
\begin{pmatrix}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33} \\
\end{pmatrix}
\begin{pmatrix}
C_{11} & C_{21} & C_{31} \\
C_{12} & C_{22} & C_{32} \\
C_{13} & C_{23} & C_{33}
\end{pmatrix}
=
\begin{pmatrix}
a & d & g \\
b & e & h \\
c & f & i
\end{pmatrix}이제 위 식의 좌변을 전개해서 우변의 각 원소를 구해 봐요.
먼저 a원소부터 구해본다면 다음과 같습니다.
\tag{2-6}
\begin{align}
a &= a_{11} C_{11} + a_{12} C_{12} + a_{13} C_{13}\\
&=a_{11}(-1)^{1+1}M_{11} -a_{12}(-1)^{1+2}M_{12} + a_{13}(-1)^{1+3}M_{13} \\
&=a_{11}M_{11} - a_{12}M_{12} + a_{13}M_{13} \color{blue}=det(A)
\end{align}전개 결과 윗 식의 세번째 줄이 행렬식 (1-3)식과 같다는 것을 알 수 있어요. 그래서 a=det(A)가 성립합니다.
이번에는 b원소를 구해보면 다음과 같아요.
\tag{2-7}
\begin{align}
b&=a_{21} C_{11} + a_{22}C_{12} + a_{23}C_{13}\\
&=a_{21}M_{11} - a_{22}M_{12} + a_{23}M_{13}\\
\end{align}그런데 위 식의 두번째 줄을 얼핏보면 행렬식처럼 보이는데요. 행렬식이 아닙니다. (1-3)식처럼 계수와 소행렬식의 아래 첨자가 모두 같아야 행렬식인데, 이 경우에는 아래첨자가 서로 다르므로 행렬식이 아니에요. 구체적인 결과를 알기 위해 위 식을 계속 전개해봐요.
\tag{2-8}
\begin{align}
b&=
a_{21}
\begin{vmatrix}
a_{22} & a_{23}\\
a_{32} & a_{33}
\end{vmatrix}
-
a_{22}
\begin{vmatrix}
a_{21} & a_{23}\\
a_{31} & a_{33}
\end{vmatrix}
-
a_{23}
\begin{vmatrix}
a_{21} & a_{22}\\
a_{31} & a_{32}
\end{vmatrix}\\
&=
a_{21}(a_{22}a_{33} - a_{23}a_{32}) - a_{22}(a_{21}a_{33}-a_{23} a_{31}) + a_{23}(a_{21}a_{32} - a_{22} a_{31})\\
&=0
\end{align}그 결과 0이 나오는 것을 알 수 있습니다. 즉 b=0이에요.
이러한 방식으로 (2-4)식의 우변 전체 원소 값을 구해보면 다음과 같아요. 각자 구해보시기 바랍니다.
\tag{2-9}
\begin{align}
&a=e=i=det(A) \\
&b=c=d=f=g=h=0
\end{align}위의 관계를 이용해 (2-5)식을 다시 표현하면 다음과 같다는 것을 알 수 있어요.
\tag{2-10}
\begin{pmatrix}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33} \\
\end{pmatrix}
\begin{pmatrix}
C_{11} & C_{12} & C_{13} \\
C_{21} & C_{22} & C_{23} \\
C_{31} & C_{32} & C_{33}
\end{pmatrix}^{t}
=
det(A)
\begin{pmatrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{pmatrix}그리고 위 식의 양변을 det(A)로 나누면 다음과 같아져요.
\tag{2-11}
\begin{pmatrix}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33} \\
\end{pmatrix}
\color{red}{
{1 \over{det(A)}}
\begin{pmatrix}
C_{11} & C_{12} & C_{13} \\
C_{21} & C_{22} & C_{23} \\
C_{31} & C_{32} & C_{33}
\end{pmatrix}^{t}
}
\color{black}
=
\begin{pmatrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{pmatrix}마지막으로 위의 빨강색을 A^{-1}로 치환하면 다음과 같습니다.
A A^{-1} = I이 결과는 우리가 구하려고 했던 (2-2)식과 같은 형태임을 알 수 있어요. 결국 어떤 행렬의 역행렬을 구하는 식은 다음과 같다는 것을 알 수 있어요.
\tag{2-12}
A^{-1} =
{1 \over{det(A)}}
\begin{pmatrix}
C_{11} & C_{12} & C_{13} \\
C_{21} & C_{22} & C_{23} \\
C_{31} & C_{32} & C_{33}
\end{pmatrix}^{t}3. 역행렬 주요 성질
3-1. 모든 정방행렬이 역행렬을 갖는 것은 아니다.
(2-12)식에서 분모에 있는 행렬식 det(A)가 0이 아니면 역행렬 A^{-1}을 구할 수 있으나, 만일 0이면 역행렬이 존재하지 않습니다.
즉, 역행렬이 존재할 조건은 다음과 같고, 역행렬이 존재한다면 그것은 유일합니다.
\tag{3-1}
det(A) \ne 03-2. 역행렬을 행렬의 앞에서 곱하든 뒤에서 곱하던 그 결과는 단위행렬로 같다.
행렬 A와 B가 있을 때 곱하는 순서를 교환하면 일반적으로 서로 같지 않습니다. 즉 행렬에서는 곱셈의 교환법칙이 보통 성립하지 않아요.
\tag{3-2}
AB \ne BA하지만 역행렬의 경우에는 예외입니다. 서로 교환해도 단위행렬이 항상 나와요.
\tag{3-3}
A^{-1}A = A A^{-1} = I3-3. AB의 역행렬은 각각의 역행렬을 구한 후 순서를 바꾸어 곱해야 한다.
행렬 A와 B를 곱한 결과의 역행렬은, 각 행렬의 역행렬을 구한 후 순서를 바꾸어 곱해야 합니다. 식으로 쓰면 다음과 같습니다.
\tag{3-4}
(AB)^{-1} = B^{-1}A^{-1}3-4. 역행렬의 역행렬은 원래 행렬이 된다.
식으로 쓰면 다음과 같습니다.
\tag{3-5}
(A^{-1})^{-1} = A3-5. kA의 역행렬은 (1/k)A^{-1}이 된다.
k를 0이 아닌 실수라고 할 때, 다음이 성립합니다.
\tag{3-6}
(kA)^{-1} = {1 \over k} A^{-1}4. 역행렬 예제
함께 예제를 풀어봐요.
4-1. 2×2 행렬의 역행렬
다음 행렬의 역행렬을 구해 보세요.
\tag{4-1}
A=
\begin{pmatrix}
2 & 1 \\
7 & 4
\end{pmatrix}이를 위해서는 (2-12)식을 적용하면 됩니다.
우선 행렬식 det(A)를 구해봐요.
\tag{4-2}
det(A) = 2 \cdot 4 - 1 \cdot 7 = 1 이번에는 여인수 행렬을 구하면 됩니다. 예를 들어 a_{11}=2인 원소에 대응하는 여인수는 A행렬에서 1행 1열을 제외하면 4만 남는데요. 그게 소행렬식 M_{11}이 되는 거에요.
\tag{4-3}
C_{11} = (-1)^{1+1} M_{11} =
\begin{vmatrix}
4
\end{vmatrix}
=4이러한 방식으로 여인수 행렬을 모두 구하면 다음과 같아요.
\tag{4-4}
\begin{pmatrix}
C_{11} & C_{12} \\
C_{21} & C_{22}
\end{pmatrix}
=
\begin{pmatrix}
4 & -7 \\
-1 & 2
\end{pmatrix}결국 A^{-1}는 다음과 같아요.
\tag{4-5}
A^{-1} = {1 \over 1}
\begin{pmatrix}
4 & -7 \\
-1 & 2
\end{pmatrix}^t =
\begin{pmatrix}
4 & -1\\
-7 & 2
\end{pmatrix}4-2. 3×3 행렬의 역행렬
이번에는 다음 행렬의 역행렬을 구해 보세요.
\tag{4-6}
B=
\begin{pmatrix}
1 & 2& 3\\
4 & 5 & 6\\
7 & 2 & 9
\end{pmatrix}여기서도 (2-12)식을 적용하면 됩니다. 이를 위해 먼저 det(B)를 구하면 다음과 같아요.
\tag{4-7}
\begin{align}
det(B) &= (1 \cdot 5 \cdot9 - 1 \cdot 2 \cdot 6) + (2 \cdot 6 \cdot 7 - 2 \cdot 4 \cdot9)+(3 \cdot 2 \cdot 4 - 3 \cdot 5 \cdot 7)\\
&=-36
\end{align}여인수 행렬도 구해야 하는데요. 예를 들어 a_{12} = 2원소에 대응하는 여인수는 행렬에서 1행 2열을 제거한 상태에서 다음 식과 같이 구하면 됩니다.
\tag{4-8}
C_{12} = (-1)^{1+2} M_{12} = -
\begin{vmatrix}
4 & 6\\
7 & 9
\end{vmatrix}
=-(36-42) = 6이런 방식으로 여인수 행렬을 모두 구하면 다음이 됩니다.
\tag{4-9}
\begin{pmatrix}
C_{11} & C_{12} & C_{13}\\
C_{21} & C_{22} & C_{23} \\
C_{31} & C_{32} & C_{33}
\end{pmatrix}
=
\begin{pmatrix}
33 & 6 & -27\\
-12 & -12 & 12\\
-3 & 6 & -3
\end{pmatrix}결국 B^{-1}는 다음과 같아요.
\tag{4-10}
\begin{align}
B^{-1} &= {1 \over {-36}}
\begin{pmatrix}
33 & 6 & -27\\
-12 & -12 & 12\\
-3 & 6 & -3
\end{pmatrix}^{t}\\[10pt]
&={1 \over {-36}}
\begin{pmatrix}
33& -12 & -3\\
6& -12& 6\\
-27& 12& -3
\end{pmatrix}\\
&=
\begin{pmatrix}
-{11 \over 12} & {1 \over 3} & {1 \over {12}}\\[5pt]
-{1 \over 6} & {1 \over 3} & -{1 \over 6}\\[5pt]
{3 \over 4} & - {1 \over 3} & {1 \over 12}
\end{pmatrix}
\end{align}