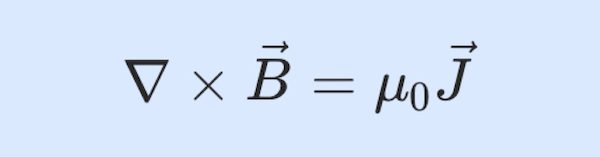Last Updated on 2025-09-17 by BallPen
앙페르 법칙으로 불리는 자기장의 회전에 대해 알아 봐요.
자기장의 회전 \nabla \times \vec B를 구해 보겠습니다.
이 개념도 아주 중요한데요. 결론부터 말씀드리면 자기장의 회전은 다음과 같습니다.
\begin{align}
\tag{D1}
\nabla \times \vec B = \mu_0 \vec J
\end{align}여기서 \vec J는 전류밀도를 의미해요. 그리고 윗 식에 스토크스 정리(Stokes’ theorem)를 적용하면 다음 식이 성립합니다.
\begin{align}
\tag{D2}
\oint \vec B \cdot d \vec l = \mu_0 I
\end{align}이 결과들은 패러데이 법칙과 비교해보면 아주 재미있어요. 구체적인 내용은 본문에서 설명드리겠습니다.
아래는 이번 글의 목차입니다.
1. (복습) 일정한 부피 전류에 의한 자기장 : 비오-사바르의 법칙
아래 [그림 1]은 부피전류에 의해 P점에 형성되는 자기장을 구하기 위한 개념도입니다.
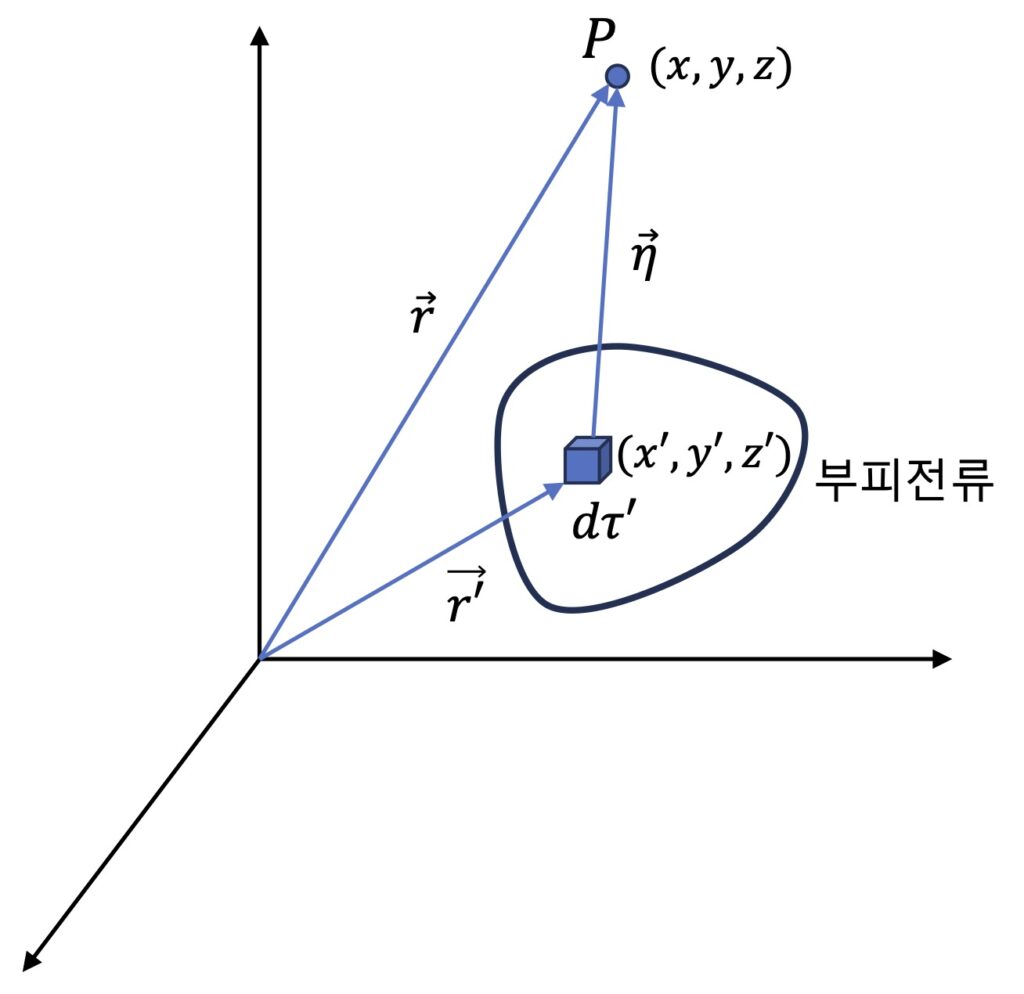
P점에서의 자기장은 비오-사바르 법칙에 의해 다음과 같이 주어집니다.
\begin{align}
\tag{1-1}
\vec B (\vec r) = {{\mu_0}\over{4\pi}} \int {{\vec J (\vec {r^{\prime}})\times \hat \eta}\over{\eta^2}} d \tau^{\prime}
\end{align}그리고 윗 식을 변형하면 다음과 같아요. 변형과정에서의 수식 전개는 이전 글을 참고하시기 바랍니다.
\begin{align}
\tag{1-2}
\vec B (\vec r) = {{\mu_0}\over{4\pi}} \Big( \nabla \times \int {{\vec J (\vec {r^{\prime}})}\over{\eta}} d \tau^{\prime} \Big)
\end{align}2. 자기장의 회전 또는 앙페르 법칙의 미분형
자기장의 회전을 구하기 위해 (1-2)식의 양변에 회전을 취해 보세요. 그러면 아래와 같습니다.
\begin{align}
\tag{2-1}
\nabla \times \vec B (\vec r) = {{\mu_0}\over{4\pi}} \nabla \times \Big(\nabla \times \int {{\vec J (\vec {r^{\prime}})}\over{\eta}}d \tau^{\prime}\Big)
\end{align}그런데 벡터 미분 연산자의 이계 미분 곱셈 규칙 중 다음 관계가 있습니다.
\begin{align}
\tag{2-2}
\nabla \times (\nabla \times \vec v) = \nabla(\nabla \cdot \vec v) - \nabla^2 \vec v
\end{align}(2-2)식의 \vec v를 \int{{\vec J (\vec {r^{\prime}})}\over{\eta}}d \tau^{\prime}와 같다고 보면 (2-1)식은 아래와 같아요.
\begin{aligned}
\tag{2-3}
\nabla \times \vec B (\vec r) &= {{\mu_0}\over{4\pi}}\Big[ \nabla {\color{red}\Big(\nabla \cdot \int {{\vec J (\vec {r^{\prime}})}\over{\eta}}d \tau^{\prime }\Big)} - {\color {blue}\nabla^2\int{{\vec J(\vec {r^{\prime}})}\over{\eta}} d\tau^{\prime }}\Big]\\[10pt]
&={{\mu_0}\over{4 \pi}} \nabla {\color{red}\Big( \int \nabla \cdot {{\vec J (\vec {r^{\prime}})}\over{\eta}} d \tau^{\prime} \Big)} - {{\mu_0}\over{4 \pi}} {\color{blue}\int \vec J(\vec {r^{\prime}}) \nabla^2 \big({1 \over \eta}\big) d \tau^{\prime}}
\end{aligned}이때 첫번째 줄의 빨강색 수식이 두번째 줄로 바뀔수 있는 이유는 \nabla는 비프라임 좌표계로 미분하지만 적분은 프라임좌표계에 대해 적분하므로 미분이 적분 안쪽으로 들어가도 상관이 없어요.
또한 첫번째 줄의 파랑색 수식이 두번째 줄처럼 바뀌는 이유는 라플라시안 \nabla^2은 비프라임 좌표계로 미분하지만 적분은 프라임 좌표계에 대해 적분하므로 \nabla^2이 적분기호 안쪽으로 들어가도 상관이 없습니다.
또한 전류밀도는 프라임 좌표계에만 의존하므로 라플라시안의 관점에서는 상수일 뿐이에요. 그래서 라플라시안 밖으로 전류밀도를 빼내었어요.
한편 (2-3)식의 두번째 줄 빨강색 수식에서 적분 안쪽은 벡터미분 연산자를 이용한 일계 미분 곱셈 규칙 중 다음의 식하고 관련이 있음을 알 수 있어요.
\begin{align}
\tag{2-4}
\nabla \cdot (f \vec v) = f (\nabla \cdot \vec v) + \vec v \cdot (\nabla f)
\end{align}이때 위 (2-4)식에서 f는 1\over \eta로, 그리고 \vec v는 \vec J(\vec {r^{\prime}})로 보면 됩니다. 그러면 (2-3)식의 적분 안쪽 부분은 다음과 같아요.
\begin{align}
\tag{2-5}
\nabla \cdot {1 \over \eta} \vec J(\vec {r^\prime}) = {1 \over \eta} ({\color{brown}\cancel{\nabla \cdot \vec J(\vec {r^\prime})}}) + \vec J(\vec {r^\prime}) \cdot (\nabla {1 \over \eta})
\end{align}그런데 위 식에서 갈색 부분의 수식은 프라임 좌표계로 표현되는 전류밀도 \vec J ({\vec {r^{\prime}}})를 비프라임 좌표계 \nabla로 미분하는 형식이에요.
그러므로 \nabla \cdot \vec J(\vec {r^{\prime}})은 상수를 미분하는 형식이기 때문에 0이 되어 버립니다.
결국 (2-5)식의 우변에서 두번째 항만이 남게 됩니다. 이를 (2-3)식에 대입하면 다음과 같아요.
\begin{aligned}
\tag{2-6}
\nabla \times \vec B (\vec {r^{\prime}}) &= {{\mu_0}\over{4 \pi}} \nabla \Big( \int \vec J (\vec {r^{\prime}}) \cdot \big ({\color{red}\nabla {1 \over \eta}}\big) d \tau^{\prime} \Big) - {{\mu_0}\over{4 \pi}} \int \vec J(\vec {r^{\prime}})\nabla^2 ({1 \over \eta})d \tau^{\prime}\\[10pt]
&={\color{red}-} {{\mu_0}\over{4 \pi}} \nabla\Big( \int \vec J (\vec {r^{\prime}}) \cdot \big ({\color{red}\nabla^{\prime} {1 \over \eta}}\big) d \tau^{\prime} \Big) - {{\mu_0}\over{4 \pi}} \int \vec J(\vec {r^{\prime}})\nabla^2 ({1 \over \eta})d \tau^{\prime}\\
\end{aligned}한편 윗 식에서 첫번째 줄의 빨강색 수식이 두번째 줄의 빨강색 수식으로 바뀌었는데요. 이것은 1 /\eta 의 기울기에 대한 다음 관계가 적용된 거에요.
\begin{align}
\tag{2-7}
\nabla \Big( {1 \over \eta} \Big) = - {{\hat \eta}\over{\eta^2}} = - \nabla^{\prime} \Big( {1 \over \eta }\Big)
\end{align}그리고 (2-6)식의 두번째 줄에서 첫번째 적분 안쪽 수식을 잘 보면 아래 식에서 갈색 수식과 같다는 것을 알 수 있어요.
\begin{align}
\tag{2-8}
\nabla ^{\prime} \cdot \Big( {{\vec J(\vec {r^{\prime}})}\over{\eta}} \Big) = {1 \over \eta} {\cancel{\nabla^{\prime}\cdot \vec J(\vec {r^{\prime}})}} + \color{brown}\vec J(\vec {r^{\prime}}) \cdot\nabla^{\prime}\Big({1 \over \eta} \Big)
\end{align}그래서 (2-8)식을 (2-6)식에 대입하면 되는데요.
그 이전에 위 (2-8)식에 있는 \nabla^{\prime} \cdot \vec J(\vec{r^{\prime}})는 0이 됩니다. 그 이유는 부피전류를 정상전류로 가정하면 전류밀도의 발산은 0이 되기 때문이에요.
결국 (2-8)식의 좌변을 (2-6)식에 대입하면 다음과 같습니다.
\begin{align}
\tag{2-9}
\nabla \times \vec B (\vec r) ={\color{black}-} {{\mu_0}\over{4 \pi}} \nabla\Big( \int \nabla^{\prime} \cdot \big({{\vec J(\vec {r^{\prime}})}\over{\eta}}\big) d \tau^{\prime} \Big) - {{\mu_0}\over{4 \pi}} \int \vec J(\vec {r^{\prime}}) {\color{blue}\nabla^2 ({1 \over \eta})}d \tau^{\prime}\\[10pt]
\end{align}그럼 이번에는 위 (2-9)식에서 파랑색 부분을 보면 라플라시안이 나오는데요. 그 부분은 델타 함수의 성질을 이용하면 다음 관계가 성립합니다.
\begin{aligned}
\tag{2-10}
\nabla^2 \Big({1 \over \eta} \Big) = - 4 \pi \delta^3 (\vec \eta) &= - 4 \pi \delta^3 (\vec r - \vec{r^{\prime}})\\[10pt]
&=-4 \pi \delta^3 (\vec{r^{\prime} }-\vec r)
\end{aligned}윗 식에서 마지막 줄이 성립하는 이유는 델타함수는 우함수이기 때문입니다.
그럼 (2-10)식을 (2-9)식에 대입하고, 또 (2-9)식의 첫번째 적분을 발산정리를 이용해 면적적분으로 바꾸면 다음의 관계가 성립함을 알 수 있어요.
\begin{aligned}
\tag{2-11}
\nabla \times \vec B (\vec r) &= - {{\mu_0}\over{4 \pi}} \nabla {\cancel{\Big( \oint {{\vec J (\vec {r^{\prime}})}\over{\eta}}\cdot d \vec a^{\prime} \Big)}} \\[10pt]
&~~~~~~~~~~~~~~~~~- {{\mu_0}\over{\cancel{4 \pi}}} ({\cancel{-4 \pi}}) \int \vec J(r^{\prime}) \delta^3 (\vec {r^{\prime}} - \vec r) d \tau ^{\prime}
\end{aligned}그런데 윗 식의 첫번째 적분은 0이 됩니다. 그 이유는 전류가 부피전류이기 때문에 표면으로 흐르는 전류가 전혀 없어요. 따라서 표면에 대한 면적적분은 0이 됩니다.
또한 윗 식의 두번째 적분에서 다음의 델타 함수 성질을 적용해봐요.
\begin{align}
\tag{2-12}
\int f(\vec r) \delta^3 (\vec r - \vec a) d \tau = f(a)
\end{align}그러면 결국 (2-11)식은 다음과 같아요.
\begin{align}
\tag{2-13}
\nabla \times \vec B (\vec r) = \mu_0 \vec J(\vec r)
\end{align}바로 윗 식을 자기장의 회전, 또는 앙페르 법칙의 미분형이라고 부릅니다.
3. 앙페르 법칙의 적분형
앞에서 말씀드린 것처럼 (2-13)식은 자기장의 회전을 구한 결과이며 이 식을 앙페르 법칙의 미분형이라고 합니다.
그러면 (2-13)식의 양변을 면적적분하고 스토크스의 정리를 적용해보도록 해요. 그러면 앙페르 법칙의 적분형을 구할 수 있습니다.
\begin{aligned}
\tag{3-1}
\int (\nabla \times \vec B) \cdot d \vec a &= \oint \vec B \cdot d \vec l \\[10pt]
&= \mu_0 \int \vec J \cdot d \vec a\\[10pt]
&=\mu_0 I_{enc}
\end{aligned}결국 다음 식이 성립합니다.
\begin{align}
\tag{3-2}
\oint \vec B \cdot d \vec l = \mu_0 I_{enc}
\end{align}윗 식은 폐곡선을 따라 자기장을 선적분하면 그 폐곡선 안쪽을 통과하는 알짜 전류 I_{enc}에 투자율을 곱한 값과 같다는 의미입니다.
(3-2)식을 앙페르 법칙의 적분형이라고 합니다.