Last Updated on 2024-01-06 by BallPen
\int {1 \over {(a^2 + x^2)^{3/2}}}dx 의 적분을 풀어보겠습니다.
1 \over {(a^2 + x^2})^{3/2} 형태의 적분을 푸는 요령을 이번 글에서 다룹니다.
전자기학이나 역학 등을 공부하다보면 간혹 나오는 적분 형태인데요. 그 부정적분 결과는 다음과 같이 주어집니다.
\tag{D1}
\begin{align}
\int{1 \over{(a^2 + x^2)^{3/2}}}dx = {x \over a^2} {1 \over{\sqrt{a^2 + x^2}}}+C
\end{align}그럼 이제부터 그 풀이과정을 설명드릴게요. 펜과 종이 준비하시고 같이 해보세요.
아래는 이번 글의 목차입니다.
1. 적분식
함수는 동일하지만 정적분으로 풀도록 하겠습니다. 식은 다음과 같아요.
\tag{1}
\begin{align}
\int_{0}^{L}{1 \over{(a^2 + x^2)^{3/2}}}dx
\end{align}2. 풀이
2-1. 치환하기
(1)식에 있는 x를 a\tan (u)로 치환하겠습니다.
\tag{2}
x= a \tan (u) = a {{\sin (u)}\over{\cos (u)}} = a \sin (u) \big(\cos (u)\big)^{-1}그리고 x의 미분 dx를 구하면 다음과 같아요. 이때 곱의 미분법을 적용하였어요.
\tag{3}
\begin{align}
dx &= a\cos (u) du \big(\cos (u)\big)^{-1} + a\sin (u)(-1)\cos(u)^{-2} \big(-\sin (u)\big)du\\[8pt]
&=adu + a \big(\sin^2 (u)\big) \big(\cos (u) \big)^{-2}\\[8pt]
&={{\cos^2(u)}\over{\cos^2 (u)}}adu + {{\sin^2 (u)}\over{\cos^2 (u)}}adu\\[8pt]
&={{(\cos^2 (u)+ \sin^2 (u))}\over{\cos^2(u)}}adu\\[8pt]
&={a\over{\cos^2 (u)}}du
\end{align}2-2. 적분하기
(2)식과 (3)식을 (1)식에 대입하고 적분합니다. 이때 적분구간을 바꿔야 하는데요. (2)식을 u에 대해 정리해봅니다.
\tag{4}
u = \tan^{-1} {{x}\over{a}}적분구간의 아래끝은 (4)식의 x대신에 0을 대입하고 위끝은 x대신에 L을 대입하면 됩니다. 그러면 아래끝은 0이 되고, 위끝은 \tan^{-1}(L/a)입니다.
\tag{5}
\begin{align}
\int_{0}^{L} {1 \over{(a^2 + x^2)^{3/2}}}dx &= \int_0^{\tan^{-1}{L \over a}} {1\over{(a^2 + a^2 \tan^2 (u))^{3/2}}} {a \over{\cos^2(u)}} du\\[8pt]
&=\int_0^{\tan^{-1}{L \over a}} {1\over{a^3(1 + \tan^2 (u))^{3/2}}} {a \over{\cos^2(u)}} du\\[8pt]
\end{align}한편 삼각함수 항등식에 따르면 다음의 관계가 성립합니다.
\tag{6}
\begin{align}
&\cos^2 (u) + \sin^2 (u) = 1\\[8pt]
&{{\cos^2(u)}\over{\cos^2 (u)}} + {{\sin^2 (u)}\over{\cos^2 (u)}} = {1 \over{\cos^2 (u)}}\\[8pt]
& \color{blue}{1+ \tan^2 (u) = {1 \over{\cos^2 (u)}}} \color{black}=\sec^2(u)
\end{align}(6)식의 파랑색 부분을 (5)식에 대입합니다. 그러면 다음과 같아요.
\tag{7}
\begin{align}
\int_{0}^{L} {1 \over{(a^2 + x^2)^{3/2}}}dx &=\int_0^{\tan^{-1}{L \over a}} {1\over{a^3(1 + \tan^2 (u))^{3/2}}} {a \over{\cos^2(u)}} du\\[8pt]
&={{a}\over{a^3}}\int_0^{\tan^{-1}{L \over a}} {1\over{1/{\cos^3(u)}}}{1\over{\cos^2 (u)}}du\\[8pt]
&={1 \over a^2} \int_0^{\tan^{-1}{L \over a}}\cos(u) du\\[8pt]
&={1 \over{a^2}} \Big[ \sin(u)\Big]_0^{\tan^{-1}{L \over a}} \\[8pt]
&={1 \over a^2 }\sin \big(\tan^{-1} {L \over a}\big)
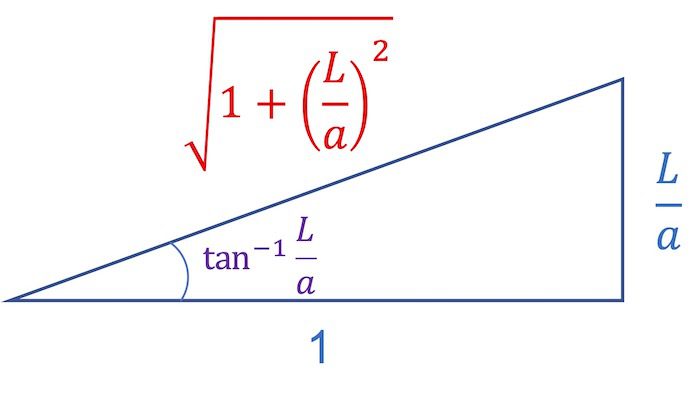
\end{align}(7)식의 가장 마지막 줄을 다른 형태로 바꾸기 위해서는 아래의 삼각형을 참고해 주세요.
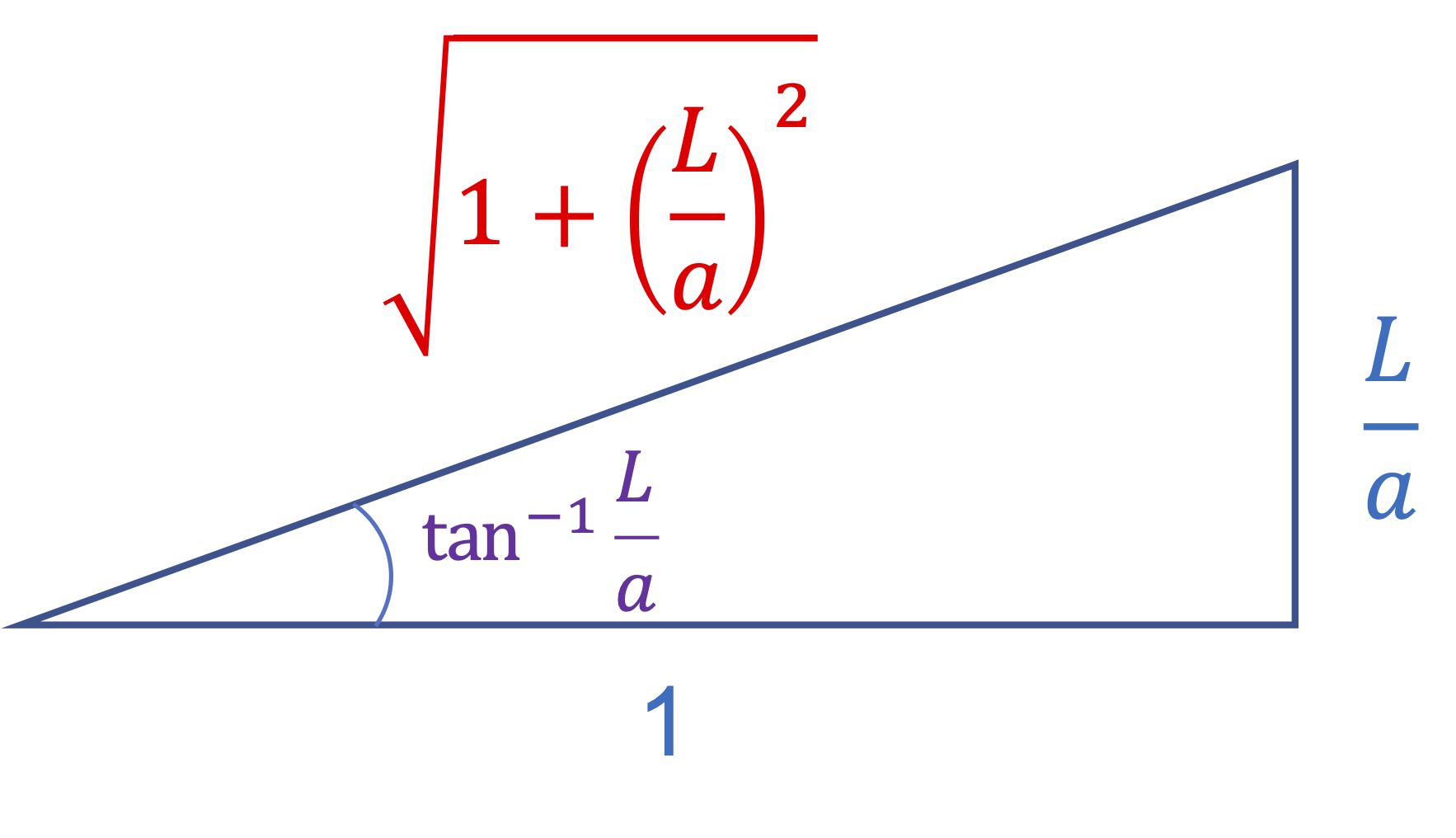
밑변이 1이고 높이가 L \over a인 직각삼각형이 있는데요. 그림에 표시한 각도가 (4)식에 주어진 u = \tan^{-1}{L \over a}입니다.
그러므로 (7)식의 가장 마지막에 주어진 식은 다음과 깉이 표현될 수 있습니다.
\tag{8}
\begin{align}
\int_{0}^{L} {1 \over{(a^2 + x^2)^{3/2}}}dx &={1 \over a^2 }\sin \big(\tan^{-1} {L \over a}\big)\\[8pt]
&={1 \over a^2} {{L/a}\over{\sqrt{1+(L/a)^2}}}\\[8pt]
&={L \over a^3} {1 \over {\sqrt{{{a^2}\over{a^2}}+{L^2 \over a^2}}}}\\[8pt]
&={L \over a^3} {1 \over {(1/a) \sqrt{a^2+ L^2}}}\\[8pt]
&={L \over a^2}{1 \over{\sqrt{a^2 + L^2}}}
\end{align}바로 (8)식의 가장 마지막 줄이 결과입니다.