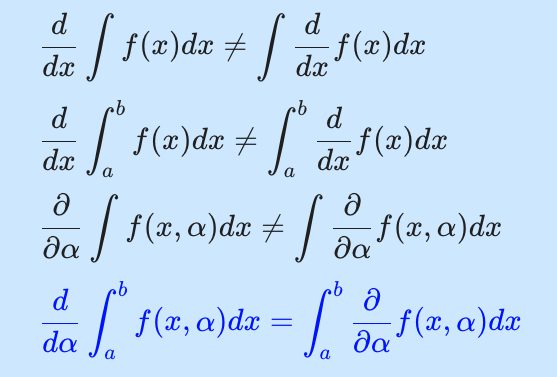Last Updated on 2024-11-16 by BallPen
함수를 적분 후 미분한 것과 미분 후 적분한 것의 결과가 같은지 알아 봐요.
어떤 함수를 적분 후 미분 또는 미분 후 적분한 결과가 같은지 궁금한 경우가 있어요. 특히 과학이나 공학 분야에서 이런 경우가 간혹 나오게 되는데요.
그 결과는 아래와 같습니다.
\begin{align*}
&{d \over dx} \int f(x)dx \ne \int {d \over dx} f(x) dx\\[8pt]
&{d \over dx} \int_a^b f(x) dx \ne \int_a^b {d \over dx} f(x)dx\\[8pt]
&{\partial \over \partial \alpha} \int f(x, \alpha) dx \ne \int {\partial \over \partial \alpha} f(x, \alpha) dx\\[8pt]
&\color {blue} {d \over d \alpha}\int_a^b f(x, \alpha) dx = \int_a^b {\partial \over \partial \alpha} f(x, \alpha) dx\\
\end{align*}상수를 적분구간으로 하는 다변수함수에 대해서는 적분과 미분의 순서가 바뀌어도 같다는 것을 알 수 있어요.
아래는 이번 글의 목차입니다.
Contents
1. 일변수 함수
변수가 하나인 어떤 함수 f(x)가 다음과 같이 주어질 때 이 함수의 적분 후 미분, 미분 후 적분을 각각 구해보겠습니다.
\tag{1-1}
\begin{align}
f(x) = 3x^2 + 2x +8
\end{align}1-1. 부정적분
[부정적분 후 미분]
먼저 부정적분 후 미분하는 경우입니다. 어떤 함수를 적분 후 미분했으니 원래 함수로 돌아올 것을 기대할 수 있을 거에요.
\tag{1-2}
\begin{align}
{d \over dx} \int f(x) dx &= {d \over dx} \int(3x^2 + 2x +8) dx\\[8pt]
&= {d \over dx} (x^3 + x^2 +8x+c)\\[8pt]
&=3x^2 + 2x + 8
\end{align}여기서 c는 적분상수를 의미합니다.
그 결과 기대했던대로 위 식과 같이 일변수 함수 f(x)를 부정적분 후 미분하면 원래 함수 f(x)로 돌아옵니다.
[미분 후 부정적분]
다음은 함수를 미분 후 부정적분하는 경우입니다.
\tag{1-3}
\begin{align}
\int{d \over dx} f(x) dx &= \int {d \over dx}(3x^2 + 2x + 8)dx\\[8pt]
&=\int (6x + 2)dx\\[8pt]
&=3x^2 + 2x +c\\
\end{align}그 결과 f(x)를 미분 후 부정적분하면 원래 함수 f(x)가 나오지 않습니다. 그 이유는 상수항이 임의의 수 c로 나오기 때문이에요.
만일 c가 어떤 특정한 값을 갖는지를 도출하고 싶다면 경계조건이 필요합니다. 예를 들어 x=2에서 (1-3)식의 좌변이 20이 되어야 한다는 조건이 있다면, 이 조건을 만족하는 c는 4가 되어야 함을 알 수 있어요.
결국 (1-2)식과 (1-3)식처럼 어떤 함수를 부정적분 후 미분한 것과 미분 후 부정적분한 결과는 서로 달라요.
\tag{1-4}
{d \over dx} \int f(x)dx \ne \int {d \over dx} f(x) dx1-2. 정적분
[정적분 후 미분]
함수 f(x)를 정적분 후 미분하는 경우입니다.
부정적분과 달리 정적분은 결과가 특정 숫자로 나오게 되잖아요. 그래서 이 숫자, 즉 상수를 미분하면 0이 나올 것 같은데요. 정말 그런지 아래 결과를 봐주세요.
\tag{1-4}
\begin{align}
{d \over dx} \int_0^2 f(x) dx &= {d \over dx} \int_0^2 (3x^2 + 2x +8) dx\\[8pt]
&={d \over dx} \Big[x^3 + x^2 + 8x \Big]_0^2\\[8pt]
&={d \over dx} (28)\\[8pt]
&=0
\end{align}기대했던 대로 0이 나옴을 알 수 있어요.
[미분 후 정적분]
다음은 함수를 미분 후 정적분하는 경우입니다.
\tag{1-5}
\begin{align}
\int_0^2 {d \over dx}f(x) dx &= \int_0^2 {d \over dx}(3x^2 + 2x +8) dx\\[8pt]
&=\int_0^2 (6x + 2)dx\\[8pt]
&=\Big[ {6 {x^2 \over 2 }} + 2x \Big]_0^2\\[8pt]
&=16
\end{align}이번에는 16이 나오는군요.
그 결과 (1-4)식과 (1-5)식처럼 f(x)를 미분 후 정적분한 값은 정적분 후 미분한 값과 다르다는 것을 알 수 있어요.
\tag{1-6}
{d \over dx} \int_a^b f(x) dx \ne \int_a^b {d \over dx} f(x)dx
2. 다변수 함수
변수가 둘인 어떤 함수 f(x, \alpha)가 다음과 같이 주어질 때 적분 후 미분, 미분 후 적분을 알아보겠습니다.
\tag{2-1}
\begin{align}
f(x) = 3x^2 + 2x +5 \alpha
\end{align}2-1. 부정적분
[부정적분 후 편미분]
함수 f(x, \alpha)를 x로 부정적분 후, \alpha로 편미분해봐요.
\tag{2-2}
\begin{align}
{\partial \over \partial \alpha} \int f(x, \alpha) dx &={\partial \over \partial \alpha} \int ({3x^2 + 2x + 5 \alpha}) dx\\[8pt]
&={\partial \over \partial \alpha} \Big( x^3 + x^2 + 5 \alpha x + c\Big)\\[8pt]
&=5x
\end{align}[편미분 후 부정적분]
이번에는 \alpha로 편미분 후 x로 부정적분 해봐요.
\tag{2-3}
\begin{align}
\int {\partial \over \partial \alpha} f(x, \alpha) dx &= \int {\partial \over \partial \alpha}(3x^2 + 2x + 5 \alpha)dx\\[8pt]
&=\int 5 dx\\[8pt]
&=5x+c
\end{align}결국 (2-2)식과 (2-3)식처럼 어떤 다변수 함수를 부정적분 후 편미분한 것과 편미분 후 부정적분한 결과는 서로 다르다는 것을 알 수 있어요.
\tag{2-4}
{\partial \over \partial \alpha} \int f(x, \alpha) dx \ne \int {\partial \over \partial \alpha} f(x, \alpha) dx
2-2. 정적분
[정적분 후 상미분]
함수 f(x, \alpha)를 x로 정적분 후, \alpha로 미분해봐요. 이때 다변수 함수 f(x, \alpha)를 x로 정적분하면 \alpha만의 함수가 되므로 편미분이 아닌 상미분을 해주어야 합니다.
\tag{2-5}
\begin{align}
{d \over d \alpha} \int_0^2 f(x, \alpha) dx &={d \over d \alpha} \int_0^2 ({3x^2 + 2x + 5 \alpha}) dx\\[8pt]
&={d \over d \alpha} \Big[ {x^3} + {x^2} + 5 \alpha x \Big]_0^2\\[8pt]
&={d \over d \alpha} (12+10 \alpha)\\[8pt]
&=10
\end{align}[편미분 후 정적분]
이번에는 f(x, \alpha)를 \alpha로 편미분 후 x로 정적분하면 다음과 같아요.
\tag{2-6}
\begin{align}
\int_0^2 {\partial \over \partial \alpha} f(x, \alpha) dx &= \int_0^2 {\partial \over \partial \alpha} (3x^2 + 2x + 5 \alpha) dx\\[8pt]
&=\int_0^2 5dx\\[8pt]
&=\Big[ 5x \Big]_0^2\\[8pt]
&=10
\end{align}놀랍게도 이 경우에는 (2-5)식과 (2-6)식이 서로 같다는 것을 알 수 있어요.
\tag{2-7}
\color {blue} {d \over d \alpha}\int_a^b f(x, \alpha) dx = \int_a^b {\partial \over \partial \alpha} f(x, \alpha) dx
다만 여기서 중요한 것은 정적분의 적분 구간이 상수인 경우에만 같아진다는 거에요. 만일 적분구간이 \alpha의 함수로 주어지면 두 결과 값은 서로 달라질 수 있어요.
이 성질은 라이프니츠 적분 규칙(Leibniz integral rule)을 통해 이해할 수 있는데요. 이 규칙에 따르면 다음의 관계가 성립합니다.
\tag{2-8}
\begin{align}
&{d \over d \alpha} \Big( \int_{a(\alpha)}^{b(\alpha)} f(x,\alpha) dx \Big)\\[8pt]
&~~~~~=f(\alpha, b(\alpha))\cdot{\color{blue}{d \over d \alpha}b(\alpha)} - f(\alpha, a(\alpha))\cdot{\color{blue}{d \over d \alpha}a(\alpha)}+\int_{a(\alpha)}^{b(\alpha)} {\partial \over \partial x} f(x, \alpha) dx
\end{align}그런데 위 식에서 적분구간인 a(\alpha)와 b(\alpha)가 상수라면 파랑색 수식 부분이 0이 됨을 알 수 있어요. 상수를 미분하는 것이니 0이 되는 것이죠.
그러면 결국 (2-8)식의 좌변과 우변이 서로 같아야 하는데 그러면 (2-7)식이 된답니다.
라이프니츠 적분 규칙에 대해서는 나중에 기회가 되면 다른 글에서 구체적으로 설명드리겠습니다.
