전치행렬(Transpose Matrix)

Last Updated on 2024-11-06 by BallPen

전치행렬을 만드는 방법과 그 성질을 알아 봐요.

전치행렬(Transpose Matrix)이란 어떤 행렬의 행과 열을 맞바꾼 행렬을 뜻합니다. 이를 기호로 쓰면 어떤 행렬 $M$ 의 전치행렬은 $M^T$ 로 표기합니다.

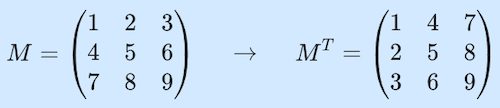
예를 들어 다음의 $3 \times 3$ 행렬 $M$ 에 대한 전치행렬 $M^{T}$ 는 다음과 같아요.

\tag{D1} M = \begin{pmatrix} 1 & 2 & 3\\ 4 & 5 & 6\\ 7 & 8 & 9 \end{pmatrix} ~~~~~ \rightarrow ~~~~~ M^{T} = \begin{pmatrix} 1 & 4 & 7\\ 2 & 5 & 8\\ 3 & 6 & 9 \end{pmatrix}

전치행렬은 직교 대각화 문제(행렬의 대각화 조건), 직교행렬등을 이해하는데 반드시 필요한 개념입니다.

이번 글에서는 전치행렬이 어떻게 정의되며 그 성질이 무엇인지 알아보겠습니다.

아래는 이번 글의 목차에요.

Contents [hide]

1. 행렬
2. 전치행렬
3. 전치행렬 성질

1. 행렬

행렬(matrix)이란 한 개 이상의 수를 직사각형 배열로 만든 것을 말합니다. 이때 숫자 배열의 가로 방향을 행, 세로 방향을 열이라고 부르죠.

행렬의 크기는 보통 $m \times n$ 이라고 표기하는데요. 여기서 $m$ 는 행의 갯수, $n$ 은 열의 갯수를 뜻합니다.

예를 들어 $1 \times 3$ 행렬, 즉 1행 3열의 크기를 갖는 행렬을 $M_1$ 이라고 할 때 그 모양은 다음과 같아요. 행렬안에 있는 $a_{11}$ , $a_{12}$ , $a_{13}$ 는 숫자(또는 식)로써 행렬의 원소라고 불리는데요. $a_{13}$ 은 1행 3열 원소를 뜻합니다.

\tag{1-1} M_1 = \begin{pmatrix} a_{11} & a_{12} & a_{13} \end{pmatrix}

이런 방식으로 $2 \times 3$ 행렬, 즉 2행 3열의 크기를 갖는 행렬은 다음과 같아요.

\tag{1-2} M_2 = \begin{pmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \end{pmatrix}

물론 $3 \times 3$ 행렬은 다음과 같겠죠.

\tag{1-3} M_3 = \begin{pmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{pmatrix}

$4 \times 3$ 행렬은 다음과 같겠죠.

\tag{1-4} M_4 = \begin{pmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \\ a_{41} & a_{42} & a_{43} \end{pmatrix}

2. 전치행렬

전치행렬이란 원래 행렬에서 행과 열을 바꾼 행렬이에요. 기호로 설명드리면 아래 (2-1)식처럼 행렬 $M$ 의 $i$ 행 $j$ 열 원소 $a_{ij}$ 를 전치하여 $j$ 행 $i$ 열 원소 위치 $a_{ji}$ 로 바꾼다는 의미입니다.

\tag{2-1} M = [a_{ij}] ~~~~~~~~~~\rightarrow~~~~~~~~~~M^{T} = [a_{ji}]

예를 들어 (1-1)식의 $1 \times 3$ 행렬을 전치행렬로 만들면 다음과 같이 $3 \times 1$ 행렬이 됩니다.

\tag{2-2} M_1 = \begin{pmatrix} a_{11} & a_{12} & a_{13} \end{pmatrix} ~~~~~~~~~~\rightarrow~~~~~~~~~~{M_{1}}^{T} = \begin{pmatrix} a_{11}\\ a_{21}\\ a_{31} \end{pmatrix}

만일 구체적 숫자를 대입한다면 다음이 되는 것이죠. 예를 들어 1행 2열에 있는 숫자 7은 전치된 행렬에서 2행 1열에 놓여지게 됩니다.

\tag{2-3} M_1 = \begin{pmatrix} 3 & 7 & 2 \end{pmatrix} ~~~~~~~~~~\rightarrow~~~~~~~~~~{M_1}^{T} = \begin{pmatrix} 3\\ 7\\ 2 \end{pmatrix}

같은 방식으로 (1-2)식에 있는 $2 \times 3$ 행렬을 전치하면 $3 \times 2$ 행렬이 될 것임을 짐작할 수 있어요. 예를 들어 다음과 같습니다.

\tag{2-4} M_2 = \begin{pmatrix} {\color {blue}8} & 6 & 9 \\ 7 & {\color{blue}1} & 4 \end{pmatrix} ~~~~~~~~~~\rightarrow~~~~~~~~~~{M_2}^{T} = \begin{pmatrix} {\color{blue}8}&7\\ 6&{\color{blue}1}\\ 9&4\\ \end{pmatrix}

이제 전치행렬 만드는 방법을 이해하셨을 거에요. 만일 이 방법이 헷갈리신다면 위에서 원래 행렬 $M_2$ 의 숫자 8과 1로 이어지는 선을 대각선축이라고 했을 때, 이 축을 중심으로 행렬을 회전시키면 전치행렬 ${M_2}^T$ 가 되는 것으로 이해하셔도 좋습니다.

같은 방식으로 (1-3)식의 $3 \times 3$ 행렬을 전치하면 다음과 같아요. 물론 파랑색으로 표기한 대각선 축을 기준으로 회전시켜도 전치행렬을 만들 수 있습니다.

\tag{2-5} M_3 = \begin{pmatrix} {\color{blue}8} & 6 & 9 \\ 7 & {\color{blue}1} & 4 \\ 6 & 0 & {\color{blue}1} \end{pmatrix} ~~~~~~~~~~\rightarrow~~~~~~~~~~ {M_3}^T= \begin{pmatrix} {\color{blue}8}&7&6\\ 6&{\color{blue}1}&0\\ 9&4&{\color{blue}1} \end{pmatrix}

마지막으로 (1-3)식의 $3 \times 4$ 행렬을 전치하면 다음과 같아요.

\tag{2-6} M_4 = \begin{pmatrix} {\color{blue}8} & 6 & 9 \\ 7 & {\color{blue}1} & 4 \\ 6 & 0 & {\color{blue}1} \\ 3 & 12 & 8 \end{pmatrix} ~~~~~~~~~~\rightarrow~~~~~~~~~~ {M_4}^T = \begin{pmatrix} {\color{blue}8}&7&6&3\\ 6&{\color{blue}1}&0&12\\ 9&4&{\color{blue}1}&8\\ \end{pmatrix}

3. 전치행렬 성질

전치행렬의 성질 몇가지를 알아보겠습니다.

3-1. 전치행렬의 전치

전치된 행렬 $A^T$ 을 다시 전치하면 원래 행렬 $A$ 로 돌아옵니다.

\tag{3-1} (A^T)^T = A

3-2. 두 행렬의 합에 대한 전치

두 행렬 $A$ , $B$ 의 합을 전치하면 각 행렬을 전치한 후 합한 것과 같습니다.

\tag{3-2} (A+B)^T = A^T + B^T

3-3. 두 행렬의 차에 대한 전치

두 행렬의 차를 전치하면 각 행렬을 전치한 후 뺄셈한 것과 같습니다.

\tag{3-3} (A-B)^T = A^T - B^T

3-4. 상수를 곱한 행렬의 전치

상수 $k$ 를 행렬 $A$ 에 곱한 후 전치하면, $A$ 의 전치 $A^T$ 에 상수를 곱한 것과 같습니다.

\tag{3-4} (kA)^T = kA^T

3-5. 두 행렬의 곱에 대한 전치

두 행렬을 곱한 후 전치하면 아래와 같습니다.

\tag{3-5} (AB)^T = B^T A^T

이에 대한 증명은 나무위키를 참고해 주세요.

흥미롭고 도움이 되는 글이었나요? 리뷰를 부탁드립니다.

[Total: 1 Average: 5]