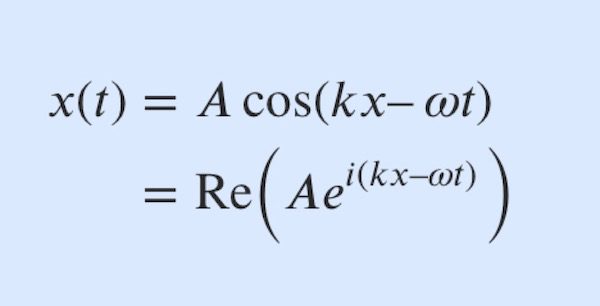Last Updated on 2025-07-25 by BallPen
진동 및 파동함수를 복소지수함수로 표현하는 방법과 그 이유를 알아 봐요.
진동 및 파동함수의 복소지수함수 표기 방법과 그렇게 표기하는 이유를 알아 봐요.
아래는 이번 글의 목차입니다.
Contents
1. 진동 및 파동함수의 복소지수함수 표기 방법
1-1. 진동함수의 복소지수함수 표기
진동이란 제자리에서 시간에 따라 물체의 변위가 주기적으로 변하는 것을 말합니다. 이를 식으로 쓰면 다음과 같아요.
\begin{align}
\tag{1}
x(t) = A \cos (\omega t – \phi)
\end{align}
여기서 \(A\)를 진폭, \(\omega\)를 진동의 각진동수, \(\phi\)를 초기위상이라고 해요. 위 식을 아래 (2)식의 삼각함수 덧셈정리를 이용해 변형해 보세요.
\begin{align}
\tag{2}
\cos(\omega t – \phi) = \cos \omega t \cos \phi + \sin \omega t \sin \phi
\end{align}
그러면 (1)식은 다음 (3)식과 같이 표기할 수 있어요.
\begin{align}
\tag{3}
x(t) &= A \cos (\omega t – \phi) \\
&= A\Big( \cos \omega t \cos \phi + \sin \omega t \sin \phi \Big)\\
&=\color{red}{A \cos \phi} \cos \omega t + \color{red}{A \sin \phi} \sin \omega t
\end{align}
이때 윗 식에서 빨강색 부분은 상수와 상수의 곱으로서 또 다른 상수가 될 뿐이므로 이를 상수 \(c_1\)과 \(c_2\)로 구분해서 표기하면 다음과 같아요.
\begin{align}
\tag{4}
x(t) = c_1 \cos \omega t + \sin \omega t
\end{align}
즉, 진동함수는 (1)식과 (4)식이 가장 기본적인 형태에요. 그런데 이것을 복소지수함수로 어떻게 표현하냐면 다음 (5)식처럼 표기합니다.
\begin{align}
\tag{5}
x(t) = A e^{i(\omega t – \phi)}
\end{align}
그런데 (1)식과 (4)식이 같다는 것은 알겠는데 (5)식과 어떻게 같은지 궁금할 거에요. 그래서 (5)식을 오일러 공식을 활용해 전개해 볼게요. 그러면 다음과 같아요.
\begin{align}
\tag{6}
x(t) &= A e^{i(\omega t – \phi)}\\
&=A \Big(\cos (\omega t -\phi) + i \sin (\omega t – \phi)\\
&=A\Big(\cos \omega t \cos \phi + \sin \omega t \sin \phi + i \sin \omega t \cos \phi – i \cos \omega t \sin \phi \Big)\\
&=A \cos \phi \cos \omega t + A \sin \phi \sin \omega t + i A \cos \phi \sin \omega t – i A \sin \phi \cos \omega t\\
&={\color{blue}{c_1 \cos \omega t + c_2 \sin \omega t}} + i c_1 \sin \omega t – i c_2 \cos \omega t
\end{align}
자 그러면 어떤가요? (6)식이 (1)식 또는 (4)식과 같은가요? 비교해보면 같지 않습니다.
그런데 (6)식의 가장 마지막 줄을 잘 보면 실수부와 허수부가 있는데 실수부(파랑색 수식 부분)의 모양이 (4)식과 같다는 것을 알 수 있어요.
이제 이해하셨을거에요.
(1)식 또는 (4)식을 (5)식의 복소지수함수로 바꾸어 표현할 수 있지만, 물리적 의미를 해석할 때에는 허수부는 무시하고 실수부만 고려해야 한다는 것을 알 수 있어요.
정리하면 다음과 같아요
\begin{align}
\tag{7}
x(t) &= A \cos (\omega t – \phi) \\
&=c_1 \cos \omega t + \sin \omega t\\
&={\rm{Re}}\Big(A e^{i(\omega t – \phi)}\Big)
\end{align}
1-2. 파동함수의 복소지수함수 표기
진동과 달리 파동은 국소적인 부분의 진동이 매질을 타고 전파해 나가는 특성이 있어요. 그래서 공간과 시간의 함수를 갖습니다. 파동함수는 다음과 같이 주어집니다.
\begin{align}
\tag{8}
y(x,t) = A \cos (kx – \omega t)
\end{align}
위 식에서 \(\cos\)을 사용하던 \(\sin\)을 사용하던 초기 위상만 차이가 있을 뿐이며 진행하는 파동에서 그것은 큰 의미가 없으므로 신경쓰지 않아도 됩니다.
이 글에서는 편의상 \(\cos\)으로 표현할께요.
그렇다면 위 (8)식의 파동함수를 복소지수함수로 표기하려면 어떻게 해야 할까요? 바로 (5)식을 그대로 적용하면 됩니다. 그러면 아래와 같아요.
\begin{align}
\tag{9}
y(x,t) = A e^{i(kx – \omega t)}
\end{align}
물론 여기서도 물리적 의미를 해석할 때에는 (9)식의 실수부만 고려해야 한다는 것을 꼭 기억하세요.
\begin{align}
\tag{10}
y(x,t) &= A \cos (kx – \omega t) \\
&={\rm{Re}}\Big(A e^{i(kx – \omega t)}\Big)
\end{align}
2. 진동 및 파동함수를 복소지수함수로 표기하는 이유
지금까지 진동 및 파동함수의 복소지수함수 표기 방법에 대해 말씀드렸어요.
그런데 이쯤에서 궁금한게 있을텐데요.
왜 굳이 복소지수함수로 표기하는지 궁금할거에요. 그 이유는 복소지수함수가 미분과 적분이 더 쉽기 때문이에요. 즉 다양한 수학적 처리가 수월하기 때문이죠.
복소지수함수로 쉽게 수학적 연산을 하고, 그 함수의 물리적 의미는 실수부만 해석하면 된다는 뜻이에요.