Last Updated on 2025-08-31 by BallPen
독립 및 종속 변수에 의존하는 다양한 함수의 미분 방법을 알아봐요.
함수의 미분 방법을 설명드립니다. 어떤 함수가 독립 및 종속 변수에 의존하는 경우 미분을 어떻게 하느냐에 관한 이야기에요.
예를 들어 독립변수를 t와 x라고 할 때 아래 함수들을 보면 독립변수에만 의존하는 경우도 있고 독립변수 뿐만아니라 종속변수에도 의존하는 경우도 있음을 알 수 있어요. 이 경우 어떻게 미분하면 될까요?
\begin{align*}
s(t), ~y(t,x), ~F \big[s(t), y(t),t \big],~G\big[s(t,x),t,x\big]
\end{align*}자연과학이나 공학 등을 공부하다 보면 참으로 다양한 함수들을 미분하게 됩니다. 그때 이 글을 참고하면 좋을 것 같아요.
아래는 이번 글의 목차입니다.
1. 미분
독립변수를 t와 x라고 할 때 아래의 함수들을 생각해봐요.
\tag{1-1}
\begin{align*}
s(t), ~y(t,x), ~F \big[s(t), y(t),t \big],~G\big[s(t,x),t,x\big]
\end{align*}앞에 있는 함수 s와 y는 독립변수 t,~x에만 의존하고, 함수 F와 G는 독립변수 t,~x 뿐만 아니라 종속변수 s,~y에도 의존합니다.
먼저 독립변수에만 의존하는 함수의 미분법을 알아보고 그 다음에 독립변수와 종속변수에 의존하는 함수의 미분법을 살펴봐요.
1-1. 독립변수에 의존하는 함수의 미분
(1-1)식에서 s(t)에 대한 미분입니다. 함수 s가 독립변수 t에 의존하는 가장 단순한 형태에요.
이 경우에는 다음과 같이 미분합니다.
\tag{1-2}
\begin{align}
ds = \Big({d s\over dt}\Big) dt
\end{align}[예제1]
함수 s(t)=2t^2 +3t+2를 미분하세요.
\tag{1-3}
\begin{aligned}
ds &= \Big[{d \over dt}{(2t^2 + 3t +2)}\Big] dt\\[10pt]
&=(4t + 3)dt
\end{aligned}이번에는 (1-1)식의 y(t,x)에 대한 미분입니다. 종속변수 y가 독립변수 t,~x에 의존하므로 각 변수별로 편미분 후에 합해주면 됩니다.
\tag{1-4}
\begin{align}
dy = \Big({\partial y \over \partial t}\Big)dt + \Big({\partial y \over \partial x}\Big)dx
\end{align}[예제2]
함수 y(t,x)= 2t^2 + 3x + 2를 미분하세요.
\tag{1-5}
\begin{aligned}
dy &= \Big[{\partial \over{\partial t}}(2t^2 + 3x +2)\Big] dt + \Big[{\partial \over {\partial x}}(2t^2 + 3x +2)\Big] dx\\[10pt]
&=4tdt + 3dx
\end{aligned}1-2. 독립변수와 종속변수에 의존하는 함수의 미분
(1-1)식에서 F\big[s(t),y(t), t\big]에 대한 미분입니다. 종속변수 s(t),~y(t)가 모두 독립변수 t에 의존하고 있어요.
이 경우 각 종속변수와 독립변수에 대한 편미분을 한 후 모두 합해주면 됩니다.
\tag{1-6}
\begin{aligned}
dF &= \Big({{\partial F} \over{\partial s}}\Big) {\color{blue}ds} + \Big({{\partial F} \over{\partial y}}\Big){\color{blue}dy} + \Big({{\partial F} \over{\partial t}}\Big)dt\\[10pt]
&=\Big({{\partial F} \over{\partial s}}\Big) {\color{blue}\Big({ds \over dt} \Big)dt} + \Big({{\partial F} \over{\partial y}}\Big) {\color{blue}\Big({dy \over dt}\Big) dt} + \Big({{\partial F} \over{\partial t}}\Big)dt\\[10pt]
&=\Big[{{\partial F} \over{\partial s}} {ds \over dt} + {{\partial F} \over{\partial y}} {dy \over dt} + {{\partial F} \over{\partial t}}\Big]dt
\end{aligned}윗 식 첫번째 줄에서 ds와 dy는 독립변수 하나에만 의존하므로 (1-2)식의 미분을 적용한거에요.
[예제3]
함수 F(s(t), y(t),t) = 3s+2y+t를 미분하세요. 이때 s=2t^2,~y=3t입니다.
이 문제를 풀기위해서는 우선 (1-2)식을 적용하여 종속변수 s(t)와 y(t)의 미분을 먼저 구해야 합니다. 이를 구하면 아래와 같아요.
\tag{1-7}
\begin{aligned}
&ds =\Big[{{d}\over{dt}}(2t^2)\Big] dt= 4t dt\\[10pt]
&dy=\Big[{{d}\over{dt}}(3t)\Big]dt=3dt
\end{aligned}이제 함수 F를 다음과 같이 미분하면 됩니다. 이때 바로 위에서 구한 미분을 대입해줍니다.
\tag{1-8}
\begin{aligned}
dF &= \Big({{\partial F}\over{\partial s}}\Big)ds + \Big({{\partial F}\over{\partial y}}\Big)dy + \Big({{\partial F}\over{\partial t}}\Big)dt\\[10pt]
&=\Big[{{\partial}\over{\partial s}}(3s+2y+t)\Big]4tdt + \Big[{{\partial}\over{\partial y}}(3s+2y+t)\Big]3dt\\[10pt]
&~~~~~~~~~~~~~~~+\Big[{{\partial}\over{\partial t}}(3s+2y+t)\Big]dt\\[10pt]
&=(3)4tdt + (2)3dt + (1)dt\\[10pt]
&=(12t+7)dt
\end{aligned}이번에는 (1-1)식의 G\big[s(t,x),t,x\big]에 대한 미분입니다. 다소 복잡해 보이지만 앞에서의 미분 규칙을 그대로 적용하면 됩니다.
\tag{1-9}
\begin{aligned}
dG &= \Big({{\partial G} \over{\partial s}}\Big) {\color{blue}ds} + \Big({{\partial G} \over{\partial t}}\Big)dt + \Big({{\partial G} \over{\partial x}}\Big)dx\\[10pt]
&=\Big({{\partial G}\over{\partial s}}\Big) {\color{blue}\Big[\Big({{\partial s}\over{\partial t}}\Big)dt+\Big({{\partial s}\over{\partial x}}\Big) dx\Big]} + \Big({{\partial G} \over{\partial t}}\Big)dt + \Big({{\partial G} \over{\partial x}}\Big)dx\\[10pt]
&=\Big({{\partial G}\over{\partial s}}{{\partial s}\over{\partial t}} + {{\partial G}\over{\partial t}}\Big)dt + \Big({{\partial G}\over{\partial s}} {{\partial s}\over{\partial x}}+{{\partial G}\over{\partial x}}\Big)dx
\end{aligned}[예제 4]
함수 G(s(t,x), t, x) = 3s+2t+4x를 미분하세요. 이때 s=3t^2 + x입니다.
이 문제를 풀기위해서는 우선 (1-4)식을 적용하여 종속변수 s(t,x)의 미분을 먼저 구해야 합니다. 이를 구하면 아래와 같아요.
\tag{1-10}
\begin{aligned}
ds &= \Big({\partial s \over \partial t}\Big)dt + \Big({\partial s \over \partial x}\Big)dx\\[10pt]
&=\Big[{{\partial}\over{\partial t}}(3t^2 + x)\Big]dt + \Big[{{\partial}\over{\partial x}}(3t^3 + x)\Big] dx\\[10pt]
&=6tdt + dx
\end{aligned}이제 함수 G를 미분하면 됩니다. 이때 바로 위에서 구한 ds를 대입하세요.
\tag{1-11}
\begin{aligned}
dG &= \Big({{\partial G} \over{\partial s}}\Big) ds + \Big({{\partial G} \over{\partial t}}\Big)dt + \Big({{\partial G} \over{\partial x}}\Big)dx\\[10pt]
&=\Big[{{\partial}\over{\partial s}}(3s+2t+4x)\Big](6tdt + dx) + \Big[{{\partial}\over{\partial t}}(3s+2t+4x)\Big]dt \\[10pt]
&~~~~~~~~~~~~~~~+ \Big[{{\partial}\over{\partial x}}(3s+2t+4x)\Big]dx\\[10pt]
&=(3)(6tdt + dx) +(2)dt + (4)dx\\[10pt]
&=18tdt + 2dt+7dx\\[10pt]
&=(18t + 2)dt + 7dx
\end{aligned}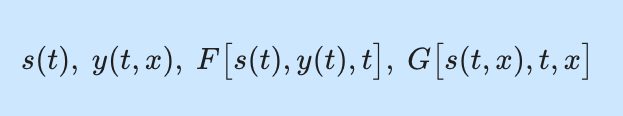


“함수의 미분 : 독립 및 종속 변수 미분”에 대한 1개의 생각