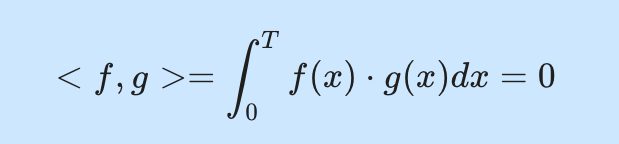Last Updated on 2024-12-14 by BallPen
삼각학수의 직교성이란 무엇인지 알아보고, 예제를 풀어 봐요.
삼각함수의 직교성 개념은 푸리에급수에서 중요한 역할을 합니다. 삼각함수가 직교성을 갖는다는 것은 어떤 삼각함수의 곱을 한 주기에 걸쳐 적분하면 0이 되는 성질을 뜻해요.
아래와 같이 두 벡터 \vec A와 \vec B 의 내적이 0이면 두 벡터가 90^{\circ}로 직교한다는 개념에 대응하는 거에요.
\begin{align*}
\vec A \cdot \vec B = AB \cos 90^{\circ} =0
\end{align*}두 함수의 내적을 공식으로 표현하면 다음과 같애요.
\begin{align*}
< f, g > = \int _0 ^T f(x) \cdot g(x)dx
\end{align*}여기서 f(x)와 g(x)가 삼각함수라면 T는 주기를 뜻하고, 두 삼각함수 f(x)와 g(x)가 서로 직교의 관계를 갖는다면 위 적분의 결과는 0이 됩니다.
\begin{align*}
< f, g > = \int _0 ^T f(x) \cdot g(x)dx = 0
\end{align*}물론 직교하지 않는다면 0이 아니겠죠. 이번 글에서는 삼각함수의 직교성에 대해 구체적으로 알아봐요.
아래는 이번 글의 목차입니다.
1. 삼각함수의 직교성 : 첫번째 예제
삼각함수의 직교성에 대한 예제로써 다음의 예를 알아봐요. 아래 식에서 m,~n은 0이 아닌 정수입니다.
\tag{1-1}
\begin{align}
< \cos\Big({{2 \pi}\over{T}} mx\Big), &\cos \Big({{2 \pi}\over{T}} nx\Big) >\\[10pt]
&= \int_0^T \Big[ \cos\Big( {{2 \pi}\over{T}} mx\Big) \cdot \cos \Big({{2 \pi}\over{T}}nx \Big) \Big]dx\\[10pt]
&= {1 \over 2} \int_0^T \Big[ \cos \Big({{2 \pi}\over{T}} (m+n) x\Big) + \cos \Big({{2 \pi}\over{T}}(m-n)x\Big)\Big] dx\\[10pt]
&={1 \over 2 } \Big[ {{T}\over{2 \pi(m+n)}}\sin \Big({{2 \pi}\over{T}}(m+n)x \Big)\\[10pt]
&~~~~~~~~~~~~+{{T}\over{2 \pi (m-n)}} \sin\Big({{2 \pi}\over{T}} (m-n)x\Big) \Big]_0^T\\[10pt]
&={1 \over 2 } \Big[ {{T}\over{2 \pi(m+n)}}\sin \Big({{2 \pi}\over{{\cancel T}}}(m+n){\cancel T} \Big)\\[10pt]
&~~~~~~~~~~~~+{{T}\over{2 \pi (m-n)}} \sin\Big({{2 \pi}\over{\cancel T}} (m-n){\cancel T}\Big) -0-0\Big]\\[10pt]
&={1 \over 2} \Big[ {{T}\over{2\pi(m+n)}} \sin\big(2 \pi(m+n)\big) \\[10pt]
&~~~~~~~~~~~~~+ {{T}\over{2 \pi (m-n)}} \sin\big( 2 \pi (m-n)\big) \Big]
\end{align}윗식의 두번째 줄에서 세번째 줄로 넘어갈 때 삼각함수 곱셈 정리 \cos \alpha \cos \beta = {1 \over 2} \Big\{ \cos(\alpha + \beta) + \cos (\alpha - \beta)\Big\}를 적용했습니다.
한편 윗식의 마지막 줄에서 m,~n이 서로 다르면 m+n과 m-n은 또 다른 정수가 됨을 알 수 있어요. 따라서 {2 \pi}의 정수배에 sin을 취한 것이 되므로 모두 0이 됨을 알 수 있어요.
즉, 다음의 직교 관계가 성립합니다.
\tag{1-2}
\begin{align}
\int_0^T \cos\Big({{2 \pi}\over{T}} mx\Big)\cdot \cos \Big({{2 \pi}\over{T}}nx\Big) dx= 0,~~~~~~when~~~m \ne n
\end{align}반면에 m=n인 경우 (1-1)식의 가장 마지막 줄에서 분모가 0이 되어 불능이 됩니다.
이 문제를 해결하기 위해 (1-1)식의 두번째 줄을 다시 정리하면 다음과 같다는 것을 알 수 있어요. 이때 m=n인 경우를 다루므로 아래 식에서 파랑색 부분의 n을 m으로 바꾸어도 상관없어요.
\tag{1-3}
\begin{align}
< \cos\Big({{2 \pi}\over{T}} mx \Big), \cos \Big({{2 \pi}\over{T}}nx\Big) > &= \int_0^T \Big[ \cos\Big( {{2 \pi}\over{T}} mx\Big) \cdot \cos \Big({{2 \pi}\over{T}}{\color {blue}m}x\Big) \Big]dx\\[10pt]
&=\int_0^T \Big[\cos \Big( {{2 \pi}\over{T}} mx\Big) \Big]^2 dx\\[10pt]
&={1 \over 2} \int_0^T \Big[1+ \cos\Big({\cancel 2} {{\cancel2} \pi \over T }mx \Big) \Big]dx\\[10pt]
&={1 \over 2} \Big[x + {{T}\over{\pi m}} \sin\Big({{\pi}\over{T}}mx \Big) \Big]_0^T\\[10pt]
&={1 \over 2} \Big[T + {{T}\over{\pi m}} \sin\Big({{\pi}\over{\cancel T}}m{\cancel T} \Big) -0-0\Big]\\[10pt]
&={T \over 2}
\end{align}위 식의 두번째 줄에서 세번째 줄로 넘어갈 때 두배각 공식인 \cos ^2 x = {1 \over 2} (1+ \cos 2x)의 관계를 적용했습니다. 또한 가장 밑에서 두번째줄에 \sin m \pi =0의 관계가 성립합니다.
결국 m=n인 경우 다음 관계가 성립하죠.
\tag{1-4}
\begin{align}
\int_0^T \cos\Big({{2 \pi}\over{T}} mx\Big)\cdot \cos \Big({{2 \pi}\over{T}}nx\Big) dx= {T \over 2},~~~~~~when~~~m = n
\end{align}따라서 위 식에서 m=n인 경우에는 두 삼각함수가 직교하지 않아요
2. 삼각함수의 직교성 : 두번째 예제
삼각함수의 직교성에 대한 또 다른 예제를 풀어봐요. 아래 식에서도 m,~n은 0이 아닌 정수입니다.
\tag{2-1}
\begin{align}
< \sin\Big({{2 \pi}\over{T}}mx \Big), &\sin \Big({{2 \pi}\over{T}}nx\Big) >\\[10pt]
&= \int_0^T \Big[ \sin\Big( {{2 \pi}\over{T}} mx\Big) \cdot \sin \Big({{2 \pi}\over{T}}nx\Big) \Big]dx\\[10pt]
&= {1 \over 2} \int_0^T \Big[ \cos({{2 \pi}\over{T}} (m+n) x\Big) - \cos \Big({{2 \pi}\over{T}}(m-n)x\Big)\Big] dx\\[10pt]
&={1 \over 2 } \Big[ {{T}\over{2 \pi(m+n)}}\sin \Big({{2 \pi}\over{T}}(m+n)x \Big)\\[10pt]
&~~~~~~~~~~~~-{{T}\over{2 \pi (m-n)}} \sin\Big({{2 \pi}\over{T}} (m-n)x\Big) \Big]_0^T\\[10pt]
&={1 \over 2 } \Big[ {{T}\over{2 \pi(m+n)}}\sin \Big({{2 \pi}\over{\cancel T}}(m+n){\cancel T} \Big)\\[10pt]
&~~~~~~~~~~~~-{{T}\over{2 \pi (m-n)}} \sin\Big({{2 \pi}\over{\cancel T}} (m-n){\cancel T}\Big) -0+0\Big]\\[10pt]
&={1 \over 2} \Big[ {{T}\over{2\pi(m+n)}} \sin\big(2 \pi(m+n)\big) \\[10pt]
&~~~~~~~~~~~~~- {{T}\over{2 \pi (m-n)}} \sin\big( 2 \pi (m-n)\big) \Big]
\end{align}여기서도 두번째 줄에서 세번째 줄로 넘어갈때 삼각함수 곱셈 정리를 적용했어요.
윗식의 마지막 줄에서 m,~n이 서로 다르면 m+n과 m-n이 또 다른 정수가 될뿐이므로 2 \pi의 정수배에 sin을 취하면 결국 모두 0이 됨을 알 수 있어요.
즉, 다음 관계가 성립합니다.
\tag{2-2}
\begin{align}
\int_0^T \sin\Big({{2 \pi}\over{T}} mx\Big)\cdot \sin \Big({{2 \pi}\over{T}}nx\Big) dx= 0,~~~~~~when~~~m \ne n
\end{align}이때 윗 식의 적분 결과가 0이므로 두 삼각함수는 서로 직교한다고 말합니다.
이번에도 m=n인 경우에는 (2-1)식 가장 마지막 줄에서 분모가 0이 되어 불능이 되어 버립니다.
이 문제를 해결하기 위해 (2-1)식의 첫번째 줄을 다시 정리하면 다음과 같아요. 이때 m=n인 경우를 다루고 있으므로 n을 m으로 하여 계산했어요.
\tag{2-3}
\begin{align}
< \sin\Big({{2 \pi}\over{T}} mx\Big), \sin \Big({{2 \pi}\over{T}}nx \Big) > &= \int_0^T \Big[ \sin\Big( {{2 \pi}\over{T}} mx \Big) \cdot \sin \Big({{2 \pi}\over{T}} {\color {blue}m}x\Big) \Big]dx\\[10pt]
&=\int_0^T \Big[\sin \Big( {{2 \pi}\over{T}} \Big) mx \Big]^2 dx\\[10pt]
&={1 \over 2} \int_0^T \Big[1- \cos\Big({\cancel 2} {{\cancel2} \pi \over T }mx \Big) \Big]dx\\[10pt]
&={1 \over 2} \Big[x - {{T}\over{\pi m}} \sin\Big({{\pi}\over{T}}mx \Big) \Big]_0^T\\[10pt]
&={1 \over 2} \Big[T - {{T}\over{\pi m}} \sin\Big({{\pi}\over{\cancel T}}m {\cancel T} \Big) -0+0\Big]\\[10pt]
&={T \over 2}
\end{align}위 식에서도 두번째에서 세번째 줄로 넘어갈 때 두배각 공식 \sin^2 x = {1 \over 2} (1- \cos 2x)를 적용하였습니다. 또한 가장 밑으로부터 두번째 줄에서 \sin \pi m =0이 됩니다.
결국 (2-3)식에 따라 m=n인 경우 다음 관계가 성립합니다.
\tag{2-4}
\begin{align}
\int_0^T \sin\Big({{2 \pi}\over{T}} mx\Big)\cdot \sin \Big({{2 \pi}\over{T}} nx\Big) dx= {T \over 2},~~~~~~when~~~m = n
\end{align}윗식의 두 삼각함수는 서로 직교하지 않아요.
