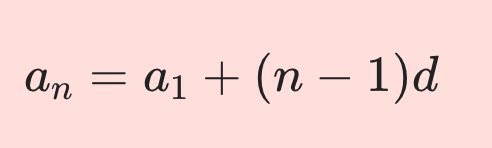등차수열의 일반항

BallPen · 2025-03-05T20:56:20+09:00

등차수열의 일반항 개념과 그 공식을 이번 글에서 구해 봐요. 일반항이란 n번째 원소가 어떤 값을 가질지를 알려주는 관계식을 뜻해요. 그래서 일반항 공식을 알 수 있다면 임의 항의 값을 쉽게 구할 수 있습니다.

Last Updated on 2025-03-05 by BallPen

등차수열의 일반항을 유도해 봐요.

등차수열의 일반항 개념을 알아보고 그 일반항을 유도해 봐요.

등차 수열(Arithmetic Sequence)이란 수열의 인접한 두 항 사이의 차이가 일정한 값을 갖는 수의 순서있는 나열을 뜻해요. 이때 $n$ 항이 어떤 값을 가질지 알려주는 식을 일반항이라고 합니다.

그래서 일반항을 알고 있으면 3번째 항, 10번째 항, 100번째 항, 어떤 항이든 그 값이 얼마가 될지를 쉽게 구할 수 있어요.

아래는 이번 글의 목차입니다.

Contents [hide]

아래는 첫째항이 $a_1$ , 공차가 $d$ 인 등차수열이라고 생각해봐요.

\tag{1-1} \{a \} = \{a_1,a_2,a_3,a_4,a_5,\cdots\}

그러면 위 수열은 다음 관계를 만족할 거에요.

\tag{1-2} \begin{align} a_2 &= a_1 + d\\ a_3 &= a_2 + d\\ a_4 &= a_3 + d\\ &~~~\vdots\\ a_{n-1} &=a_{n-2} + d\\ a_n &= a_{n-1} + d \end{align}

이때 우리가 구하고자 하는 것은 위 식에서 $a_n$ 를 구하고 싶은 거에요. 이를 구하기 위해 위 식에서 좌변끼리 합하고 우변끼리 모두 합해 봐요.

그러면 다음과 같을 거에요.

\tag{1-3} \begin{align} &{\cancel {a_2}} + {\cancel {a_3}} +{\cancel{a_4}} \cdots+{\cancel{a_{n-1}}}+a_n \\ &~~~~~~~~~~~~~= a_1 + d + {\cancel {a_2}} + d + {\cancel{a_3}} +d \cdots+ {\cancel{a_{n-2}}}+d + {\cancel {a_{n-1}}} + d \end{align}

좌변과 우변의 많은 항들이 서로 소거되는데요. 남는 항들만 정리하면 다음과 같아요.

\tag{1-4} a_n = a_1 + (n-1)d

바로 윗 식이 등차 수열의 일반항입니다. 이때 주의할 것은 $d$ 가 총 $n$ 개가 아니고 $(n-1)$ 개라는 거에요.

등차 수열의 일반항을 이용하면 우리가 원하는 항의 값을 쉽게 구할 수 있어요.

예를 들어 $n=50$ 인 항의 값은 (1-4)식의 $n$ 에 50을 대입하고, 수열의 첫째항 $a_1$ 과 공차 $d$ 를 대입하면 됩니다.

만일 첫째항 $a_1$ 이 3이고 공차 $d$ 가 4라면 그 수열의 $n=50$ 항은 다음과 같아요.

\tag{2-1} a_{50} = 3 + (50-1)4 = 199

흥미롭고 도움이 되는 글이었나요? 리뷰를 부탁드립니다.

[Total: 1 Average: 5]