Last Updated on 2022-05-28 by BallPen
각도와 관련된 용어는 무척 많고 헷갈립니다. 각각의 개념에 대해 완전히 이해해 볼까요?
각도 관련 용어로는 평면각, 입체각, 60분법, 호도법, 라디안, 스테라디안 등이 있는데요. 우선 각 용어를 정리한 후 세부 개념을 알아보겠습니다.
이번 글의 목차는 다음과 같습니다.
Contents
1. 각도 용어 정리
각도는 평면에서의 각도와 입체에서의 각도로 나눌 수 있습니다. 이때 평면 각도는 평면각, 입체 각도는 입체각으로 줄여서 말합니다.
평면각은 2가지 방법으로 정의되는데요. 사람들이 많이 사용하는 60분법, 과학 및 공학자들이 사용하는 호도법이 있습니다. 입체각은 호도법 개념을 확장하여 정의됩니다.
평면각의 단위는 \mathrm{^{\circ}}, rad이 사용되고 입체각의 단위는 sr이 사용됩니다. 각각 ‘도(또는 디그리)’, ‘라디안’, ‘스테라디안’으로 읽으면 됩니다.
아래의 표는 각도 용어를 정리한 것입니다.
| 구분 | 평면 각도 #1 | 평면 각도 #2 | 입체 각도 |
|---|---|---|---|
| 명칭 | 평면각 | 평면각 | 입체각 |
| 정의 방법 | 60분법 | 호도법 | (호도법 개념 확장) |
| 단위 표기 | \mathrm{^\circ} | rad | sr |
| 단위 명칭 | 도 (디그리) (degree) | 라디안 (radian) | 스테라디안(steradian) |
아래 [사진 1]은 어떤 방송사의 아침 방송 화면인데요.
화면 아래쪽에 울산지역의 기상정보를 알려주고 있습니다. 그런데 단위가 틀렸죠. 온도 단위 \mathrm{^{\circ} C}가 아닌 평면각 단위 \mathrm{^\circ}를 사용하고 있습니다.

예전보다는 많이 개선되었습니다만, 아직도 방송에서 단위를 틀리는 경우가 간혹 있습니다. 올바른 단위 표기법을 알고 지켜야 합니다.
그럼 이제부터 평면각과 입체각에 대한 세부 개념을 살펴 보겠습니다.
2. 평면각
거미는 보통 평면에 거미줄을 만듭니다. 물론 3차원 공간에 복잡한 거미줄을 만드는 거미도 있습니다만, 아래 [사진 2]에 있는 거미줄은 거의 평면 상태로 볼 수 있을 것 같아요.

그런데 사진에서 보는 것처럼 거미줄은 원형과 직선형의 거미줄이 서로 엮여 있는데요. 원의 중심으로부터 지름 방향을 향하는 직선형의 거미줄은 일정한 평면 각도 간격으로 배치되어 있어요.
이때 평면각은 60분법으로 정의하는 평면각과 호도법으로 정의하는 평면각이 있어요.
2-1. 60분법으로 정의하는 평면각
60분법으로 정의하는 평면각은 일반 사람들이 주로 사용하는 각도 표기법입니다. 아래의 [그림 1]과 같이 60분법은 원을 60의 6배인 360 조각으로 분리한 후 한 조각의 각도를 1\mathrm{^\circ}(도)로 정의합니다.
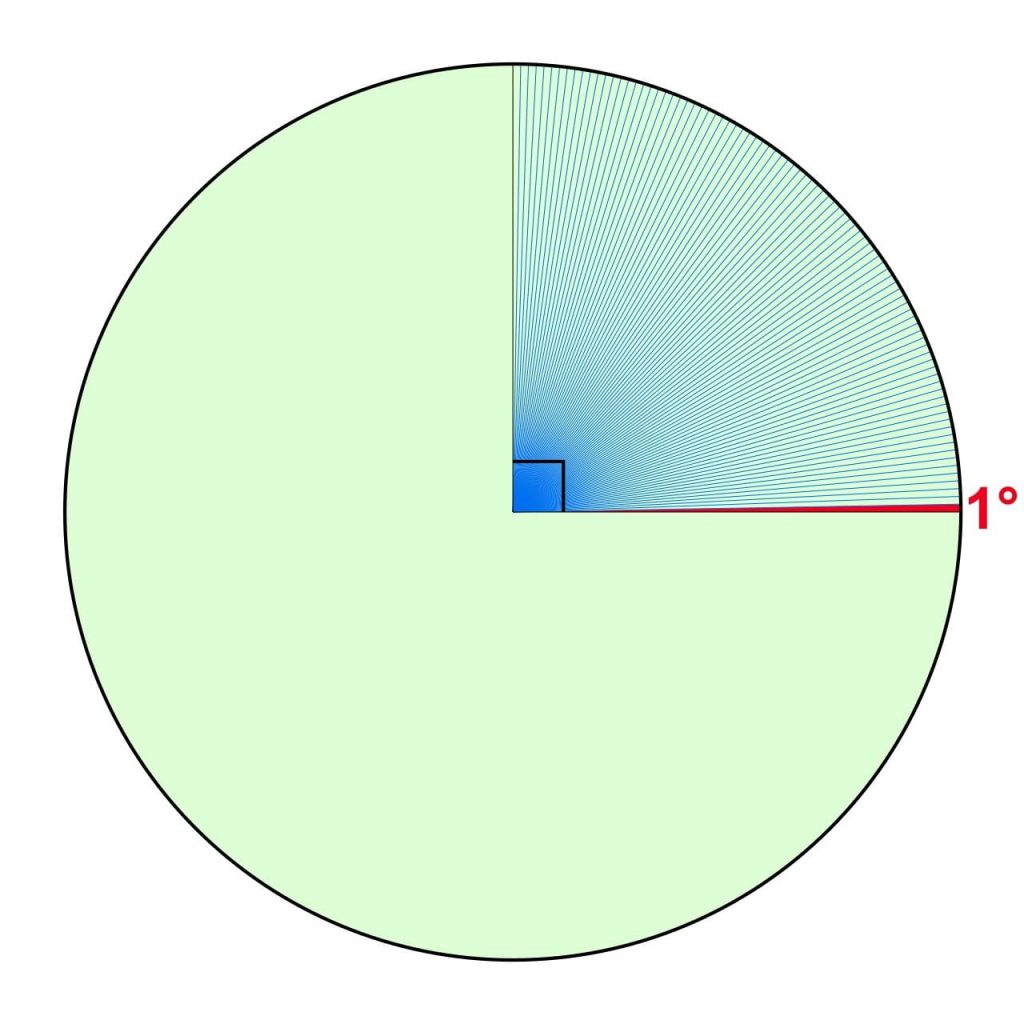
그리고 1\mathrm{^\circ}는 다시 60^{\prime}(분), 1^{\prime}(분)은 다시 60^{\prime \prime}(초)로 나눕니다.
이때 1\mathrm{^\circ}(도)가 60^{\prime}(분)이라 60분법이라 부릅니다. 그런데 왜 원을 360\mathrm{^\circ}로 했는지, 그리고 1\mathrm{^\circ}(도)를 60^{\prime}(분)으로 정했는지의 이유는 확실히 알려져 있지 않습니다.
단지 고대 달력에서 1년을 360일로 잡았고 그중의 하루에 대응하는 각도를 1^{\circ}로 한 것이라는 설이 있습니다. 또한 당시에 사용하던 60진법이 현재까지 일부 전해져 오는 것으로 보고 있어요.
아래 [그림 2]와 [그림 3]은 각도의 범위에 따른 직각, 예각, 둔각, 평각, 요각을 나타냅니다.
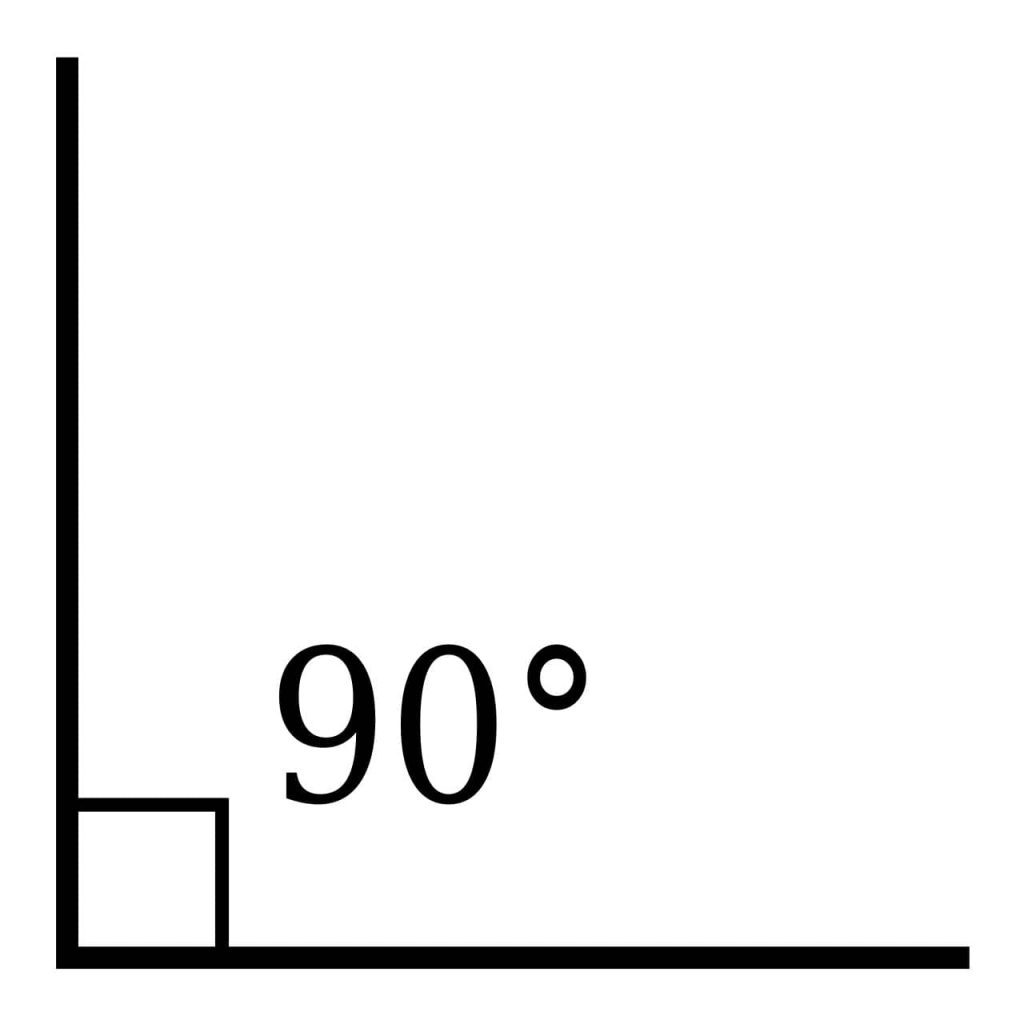
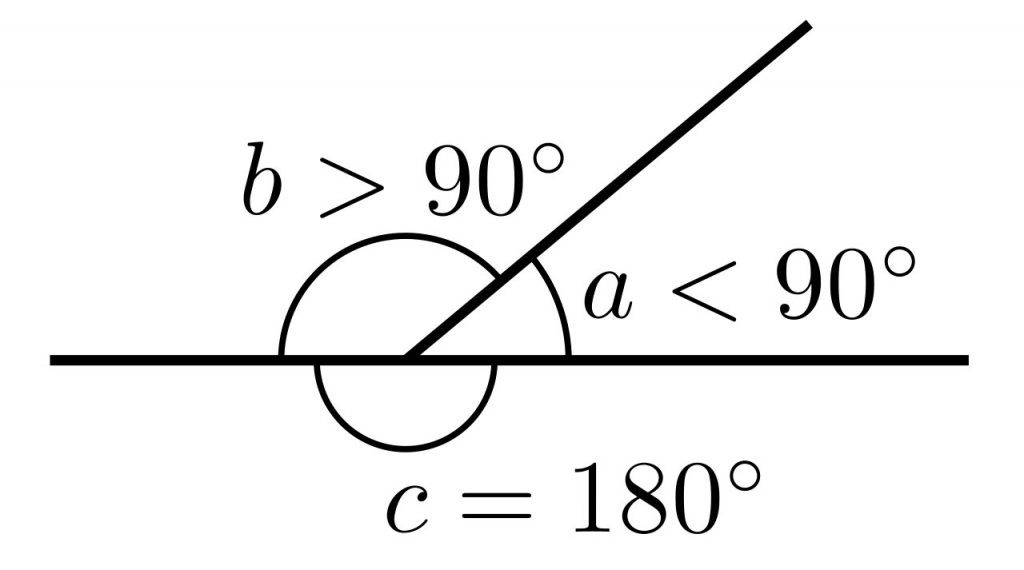
2-2. 호도법으로 정의하는 평면각
60분법이 과학적 근거 없이 관습적으로 사용되는 것에 비해 호도법은 자연과학적 사실에 근거합니다.
아르키메데스(Archimedes, 기원전 287년 경 ~ 기원전 212년 경)는 원주율의 근사값을 계산하였습니다. 여기서 원주율이란 [그림 4]에 나타낸 것처럼 원둘레 길이인 원주 C와 원의 지름 d 사이의 비율을 말하며 그 값은 식(1)과 같이 \pi가 됩니다.
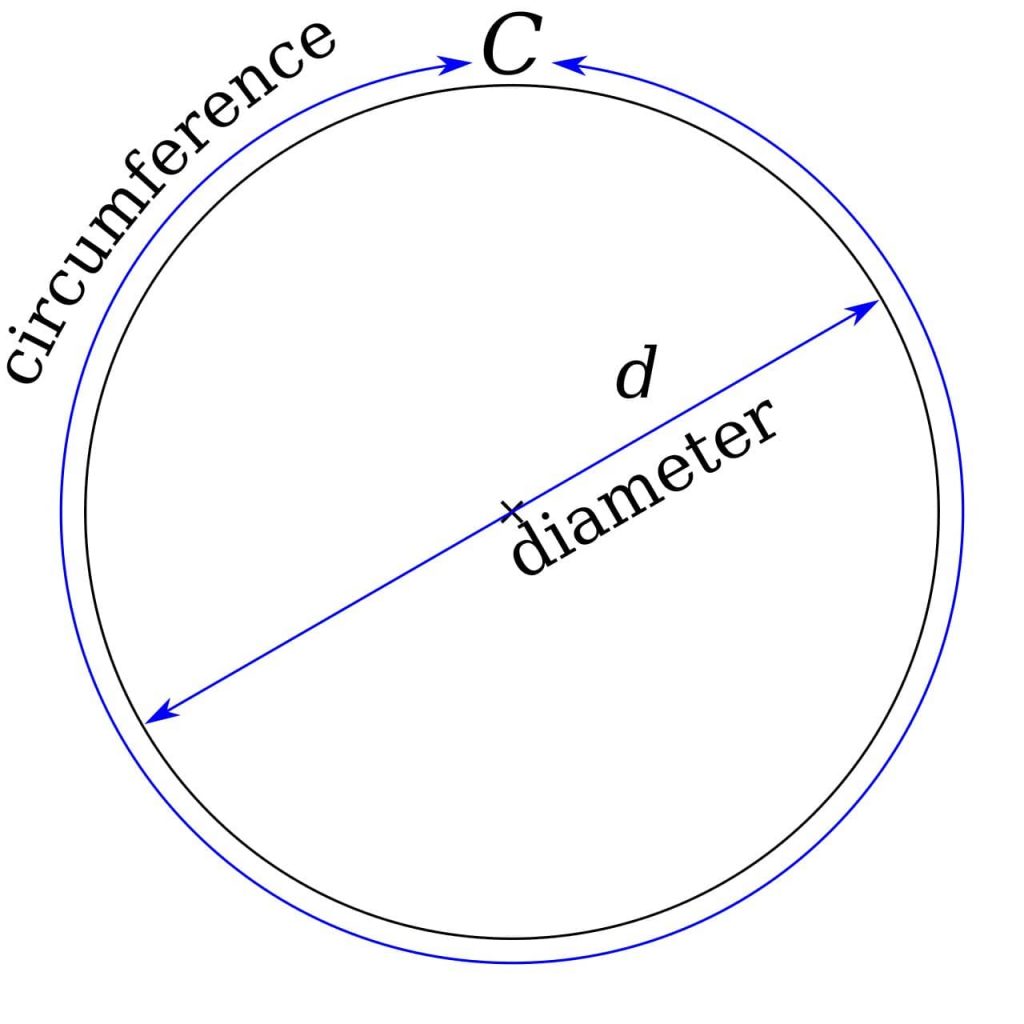
\tag{1}
원주율 = {{원주}\over{지름}} = {{C}\over{d}}= \pi
그런데 우리는 원의 지름보다는 원의 반지름을 더 많이 사용하잖아요. 그래서 반지름 r을 이용하여 표현하면 아래와 같습니다.
\tag{2}
\begin{align}
&원주율 ={{C}\over{d}} = {{C}\over{2r}} = \pi\\
\end{align}\tag{3}
{{C}\over{r}} = 2 \pi(3)식과 같이 원의 크기와 무관하게 원주 C와 반지름 r의 비율은 2\pi인 상수가 도출됩니다. 이 특성을 이용하여 원의 한 바퀴를 2\pi라는 각도로 정의하면 좋겠습니다. 즉 60분법에서 원의 한바퀴를 360{^\circ}로 정한 것과 같은 개념이죠.
그러면 임의의 각 \theta는 (3)식과 동일한 방법으로 원주의 일부인 호의길이 s와 반지름 r의 비율로 정할 수 있을 것입니다. 이와 같이 호의 길이를 이용한 각도법을 호도법이라 합니다.
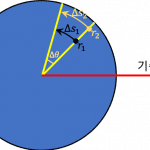
호도법에 따르면 아래 [그림 5]에 주어진 각도 \theta는 (4)식으로 정의되며, 비율값이지만 편의를 위해 단위를 [rad]으로 표기하고 ‘라디안’이라 읽게 됩니다.
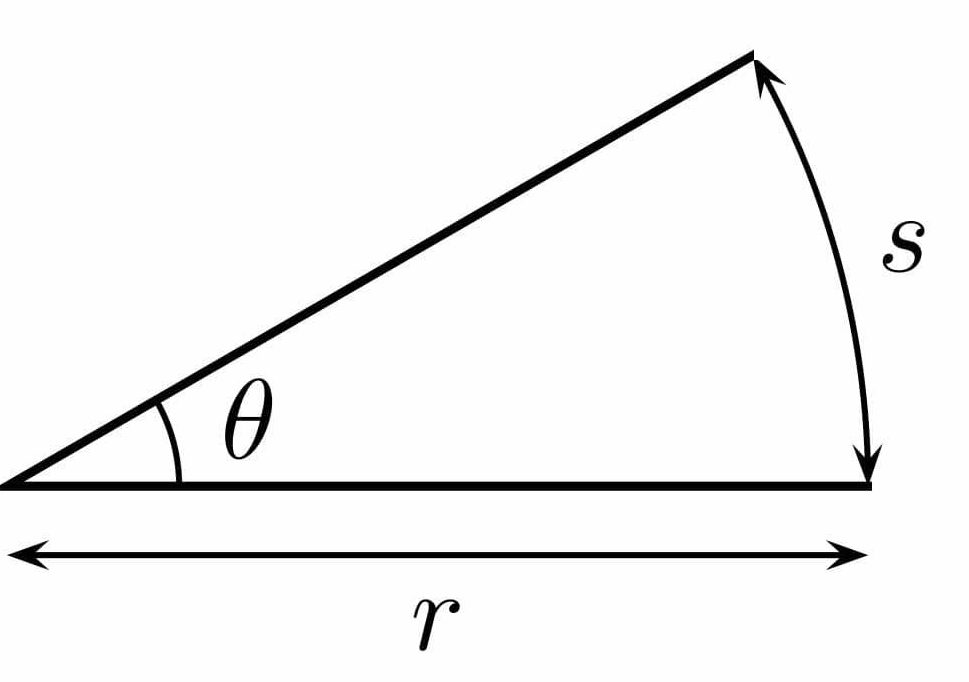
\tag{4}
\theta = {{s}\over{r}} ~~~[\mathrm{rad}](4)식의 호도법을 이용하면 우리가 원하는 모든 각도를 표기할 수 있습니다. 아래 [그림 6]의 시뮬레이션은 호도법을 이용하여 여러 각도가 구해지는 과정을 보여줍니다.

[그림 6]과 같이 원의 반지름 r과 호의 길이 s가 같으면 1 rad이고, 호의 길이가 반지름의 2배가 되면 2 rad입니다. 호의 길이가 반지름의 3배가 되면 3 rad이 됩니다. 아울러 한바퀴가 2\pi rad 이므로 반바퀴의 각도는 \pi rad, 즉 3.14 rad이 되는 것입니다.
호도법을 사용하면 원의 반지름과 각도를 알고 있는 경우 호의 길이를 쉽게 구할 수 있습니다. (4)식을 호의 길이 s로 풀면 다음과 같습니다.
\tag{5}
s=r \theta만일 r = 3.0 cm이고 \theta = 5.0 rad인 경우 호의 길이 s는 15 cm가 됩니다.
\tag{6}
\begin{align}
s &= (3.0~\mathrm{cm}) \times (5.0~\mathrm{rad}) \\
&= 15~\mathrm{cm}
\end{align}2-3. 평면각 사이의 단위 변환
{^{\circ}}를 rad으로 변환하기
예를 들어 94^{\circ}를 \mathrm{rad}으로 변환할 때 환산인자로서 \pi~{\mathrm{rad}}=180^\circ의 관계를 사용합니다.
\tag{7}
\begin{align}
94{^\circ} &= 94{^\circ} \times \big( {{\pi~{\mathrm{rad}}}\over{180^\circ}} \big) \\
&\approx 1.6~ \mathrm{rad}\\
\end{align}rad을 {^{\circ}}로 변환하기
예를 들어 2.2 rad을 ^{\circ}로 변환할 때 동일한 환산인자를 사용하면 됩니다. 다만 단위 rad이 약분되어야 하므로 환산인자의 역수를 적용합니다.
\tag{8}
\begin{align}
2.2~{\mathrm{rad}} &= 2.2~{\mathrm{rad}} \times \big( {{180^\circ}\over{\pi~\mathrm{rad}}} \big) \\
&\approx 126.1^\circ
\end{align}3. 입체각
입체각은 말그대로 입체적인 각도입니다. 호도법의 원리를 3차원 공간으로 확장한 것입니다.

위 [사진 3]은 교통꼬깔콘인데요. 꼬깔콘의 뾰족한 끝을 구의 중심이라고 했을 때 꼬깔콘의 전체적인 모양은 구의 한 부분으로 볼 수 있을 것입니다. 이때 꼬깔콘 안쪽에 형성되는 3차원적인 입체적 각도를 입체각이라 합니다.
아래 사진은 호박꽃인데요. 호박꽃도 입체각을 갖고 피는 것으로 볼 수 있어요. 그 밖에 빛의 광도 계산을 위해서도 입체각이 활용됩니다.

이와 같이 입체각은 평면각과 달리 입체적인 공간에서의 각도 개념입니다. 아래 [그림 7]은 구의 모양을 나타냅니다. 공과 같은 물체가 구입니다.
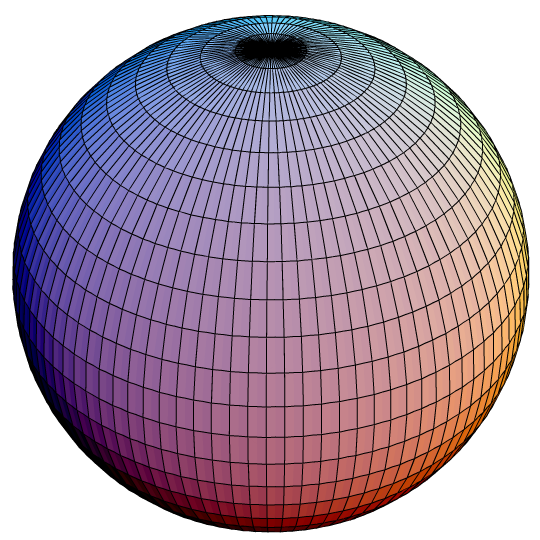
반지름 r인 구의 전체표면적 S는 다음 (9)식과 같이 주어집니다. 그리고 그 식을 조금 변형하면 (10)식과 같이 표현할 수 있어요.
\tag{9}
S= 4 \pi r^2\tag{10}
{{S}\over{r^2}} = 4 \pi따라서 구의 전체 표면적 S와 r^2의 비율은 4\pi라는 상수값을 가집니다. 이 특성을 이용하여 구의 한바퀴를 4\pi라는 입체적인 각도로 정의할 수 있어요. 호도법에서 원의 한바퀴를 2\pi rad로 고정했던 것처럼요.
그러면 임의의 입체각 \Omega는 (10)식과 동일한 방식을 적용하여 구의 일부 표면적 A와 반지름 r^2의 비율로 정할수 있을 거에요. 이러한 방법에 따르면 입체각 \Omega는 다음의 (11)식으로 정의되며, 비율값이지만 편의를 위해 단위를 [sr]로 표기하고 스테라디안이라 읽게 됩니다.
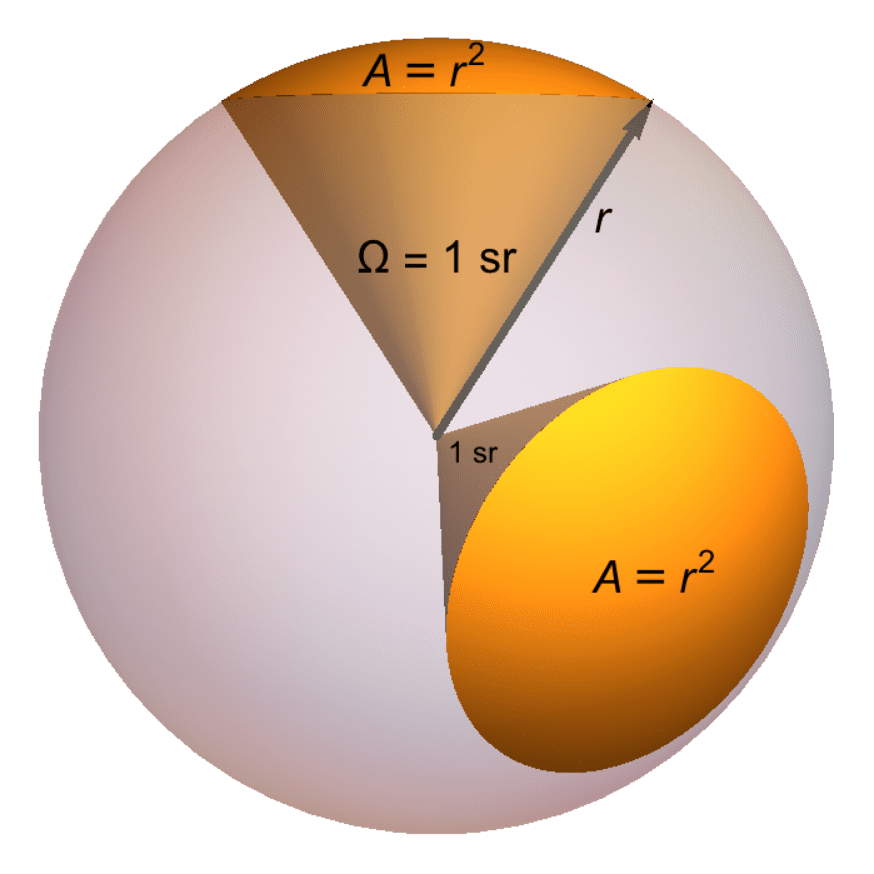
\tag{11}
\Omega = {{A}\over{r^2}}~~~[\mathrm{sr}]입체각은 원의 일부 표면적 A와 r^2의 크기가 같으면 1 sr이고, 표면적이 r^2의 2배가 되면 2 sr입니다. 표면적이 r^2의 3배가 되면 3 sr이 됩니다. 아울러 구는 4\pi sr이므로 구의 절반(반구)은 2\pi sr이 되는 것입니다.
입체각을 사용하면 구의 반지름과 입체각을 알고 있는 경우 입체각이 만드는 구의 일부 표면적을 쉽게 구할 수 있습니다. (11)식을 구의 일부 표면적 A로 풀면 다음과 같습니다.
\tag{12}
A=\Omega r^2만일 r = 3.0 cm이고, \Omega = 8.0 sr인 경우 A는 72 cm2가 됩니다.
\tag{13}
\begin{align}
A &= (8.0~\mathrm{sr}) \times (3.0~\mathrm{cm})^2 \\
&=72~\mathrm{cm^2}
\end{align}4. 각도 개념의 요약 정리
- 60분법으로 정의된 평면각은 원을 360^{\circ}로 나누고 1\mathrm{^\circ}는 다시 60^{\prime}(분), 1^{\prime}(분)은 다시 60^{\prime \prime}(초)로 나눕니다.
- 호도법으로 정의된 평면각은 원호의 길이와 원의 반지름 사이의 비율로 정의합니다. 단위는 rad을 사용합니다.
- 입체각은 구의 일부분이 갖는 표면적과 구의 반지름을 제곱한 값과의 비율로 정의합니다. 단위는 sr을 사용합니다.