Last Updated on 2022-03-18 by BallPen
유효 숫자 계산을 위한 몇 개의 예제를 풀어 보겠습니다.
유효 숫자 계산 예제 를 다양하게 풀어보는 것은 아주 중요합니다. 혹시 유효숫자에 대해 구체적으로 알고 싶으면 이곳을 우선 방문하세요.
몇가지 예제를 다루어 보겠습니다.
주어진 문제를 잘 모르겠더라도 신경쓰지 마시고 풀이과정에서 유효 숫자를 어떻게 처리했는지만 보세요.

1. 덧셈과 뺄셈에 대한 유효 숫자 계산 예제
(문제1) x방향으로 92.76 km를 이동 한 후, 그 다음에 같은 방향으로 20.0 km를 이동하였다. 전체 이동거리 s는 얼마인가?
(풀이)
총 이동거리 s를 구한다.
\tag{1}
\begin{align}
s &= s_1 + s_2 \\
&=92.76~ \mathrm{km} + 20.0~ \mathrm{km}\\
&= 112.8~ \mathrm{km}
\end{align} (유효 숫자 해설) 92.76에서 소수점 아래의 자리수가 2개이고, 20.0에서 소수점 아래의 자리수는 1개입니다. 그러므로 두 숫자를 합한 112.76에서 소수점 아래의 자리수가 1개가 되도록 기재합니다. 그러므로 결과 값은 112.8입니다.
2. 곱셈과 나눗셈에 대한 유효 숫자 계산 예제
(문제2) 물체의 무게가 3.00 \times 10^2 ~\mathrm{N}이고 중력가속도가 9.8 \mathrm{m/s^2}이다. 물체의 질량은 얼마인가?
(풀이)
무게의 정의 w=mg로부터 물체의 질량을 구한다.
\tag{2}
\begin{align}
m &= {{w}\over{g}}\\
&= {{3.00 \times 10^2 ~\mathrm{N}}\over{9.8~\mathrm{m/s^2}}}\\
&= 30.6 ~\mathrm{kg}
\end{align}(유효 숫자 해설) 3.00 \times 10^2 은 총 유효 숫자가 3개이고, 중력가속도 9.8은 총 2개입니다. 그러나 중력가속도는 상수이므로 유효 숫자를 무한대로 간주합니다. 두 숫자를 나눈 30.61224에서 총 유효 숫자 3개로 기재합니다. 그러므로 결과 값은 30.6입니다.
3. 유효 숫자 혼합 계산 예제
(문제3) 다음은 일-에너지 정리에 대한 문제 풀이 입니다. 주어진 값을 이용하여 풀어 보세요.
\tag{3}
\begin{align}
W &= {{1}\over{2}} kx^2 - wh \\
&= {{1}\over{2}} (1.000 \times 10^6 ~\mathrm{N/m}) (0.30~\mathrm{m})^2 \\
&~~~~~~~~- (13~200~\mathrm{N})(10.00~\mathrm{m})\\
&= 4.5 \times 10^4 ~\mathrm{J} - 1.32 \times 10^5 ~\mathrm{J}\\
&= 0.45 \times 10^5 ~\mathrm{J} - 1.32 \times 10^5 ~\mathrm{J}\\
&=-0.87 \times 10^5 ~\mathrm{J}\\
&=-8.7 \times10^4 ~\mathrm{J}\\
\end{align}(풀이)
(유효 숫자 해설)
문제 풀이의 두번째 행을 설명드리겠습니다.
1.000 \times 10^6의 총 유효 숫자는 4개이고 0.30의 총 유효 숫자가 2개 입니다. 1/2은 상수이므로 유효 숫자는 무한대로 보면 됩니다.
그러므로 곱과 나눗셈으로 이루어진 첫번째 항의 연산은 총 유효 숫자가 작은 2개에 맞추면 됩니다. 계산하면 45 000이 나오는데 4.5 \times 10^4으로 표기하면 됩니다.
두번째 항의 연산에서 13 200의 총 유효숫자는 3개이고, 10.00은 총 4개의 유효숫자를 갖습니다. 그러므로 곱을 통해 계산하면 132 000이 나오는데 총 3개의 유효 숫자로 표기하면 됩니다.
결국 1.32 \times 10^5이 되는 것이죠.
그리고 밑에서 세번째 줄이 밑에서 두번째 줄로 변화되는 내용을 설명드립니다. 0.45 \times 10^5에서 소수점 아래의 자리수는 2개이고 1.32 \times 10^5에서 소수점 아래의 자리수도 2개입니다.
덧셈이나 뺄셈에서는 소수점 아래의 자리수가 작은 것에 맞추므로 소수점 아래의 자리수가 2개가 되도록 표기하면 됩니다. 결국 -0.87 \times 10^5 으로 표기하면 됩니다.

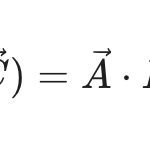
혹시 이거 수업 자료로 활용해도 될까요 .. ??
방문해 주셔서 감사합니다. 네 활용하셔도 됩니다.
중력가속도 역시 결국은 실험적으로 측정된 값이니까 유효 숫자가 2개인 걸로 볼 수도 있지 않나요? 아니면 그냥 관용적으로 중력가속도 측정 값은 유효 숫자가 무한 개라고 보는 건가요?
seok님 저의 블로그를 방문해주셔서 감사합니다.
우리가 어느 식을 이용해 문제를 풀기 위해서는 독립변수, 보통 x를 식에 대입하고 그 결과값 y를 종속변수로 얻게 되잖아요. 물론 독립변수가 둘 이상인 경우도 있겠습니다만, 중요한 것은 독립변수를 제외한 식을 구성하는 나머지 요소들은 모두 신뢰할 수 있는 값으로 보아야 할거에요. 그래야 독립변수 만의 변화에 따른 종속변수의 변화를 계산할 수 있겠죠. 그래서 식에서 나오는 중력가속도, 전자의 질량, 물건을 셈한 갯수 등의 상수들은 신뢰할 수 있는 값으로 보고 무한의 유효숫자를 갖는 것으로 간주됩니다. 물론 누가 계산을 위해 사용한 중력가속도 값이 얼마였냐고 묻는다면 정확히 알려주어야겠죠.
또한 말씀하신대로 중력가속도는 실험적으로 측정됩니다. 중력가속도 자체를 실험적으로 구하고 이를 표기하는 과정이라면 중력가속도도 유효숫자를 고려하여 숫자가 기재되어야 할 것입니다. 감사합니다.
감사합니다 유효숫자 공부하는데 도움이 됐습니다.