Last Updated on 2024-07-16 by BallPen
이심률에 따른 궤도의 모양을 알아봐요.
궤도 이심률(orbital eccentricity)이란 행성의 궤도모양을 결정하는 값을 말합니다.
중력이 작용하는 상황에서 궤도 방정식을 만든 후 그 방정식을 풀면 회전각도 \theta의 함수로서 원점으로부터 행성까지의 거리 r(\theta)를 도출할 수 있어요.
결과 식의 모양은 다음과 같아요.
\begin{align}
r = {{\alpha}\over{1 + \epsilon \cos \theta}}
\end{align}여기서 \alpha는 상수이고, \epsilon은 이심률이라 불리는 값으로, 이 값에 따라 궤도 모양이 달라집니다.
결론부터 말씀드리면 이심률 값에 따라 다음의 궤도를 갖게 됩니다.
\tag{2}
\begin{align}
&\epsilon = 0~~~~~~~~~~~~~~~~~~원궤도\\
&0<\epsilon < 1 ~~~~~~~~~~~타원궤도\\
&\epsilon = 1 ~~~~~~~~~~~~~~~~~~포물선궤도\\
&\epsilon > 1 ~~~~~~~~~~~~~~~~~~쌍곡선궤도\\
\end{align}이번 글에서는 실제로 \epsilon값에 따른 궤도의 모양을 매스매티카로 작도해보겠습니다.
아래는 이번 글의 목차에요.
Contents
1. 궤도 이심률이 0 경우 : 원 궤도
(1)식에 이심률 \epsilon = 0, \alpha=10을 대입하면 아래 그림과 같이 원형 궤도가 됩니다.
그림을 그리기 위해 사용된 매스매티카 코드는 다음과 같아요.
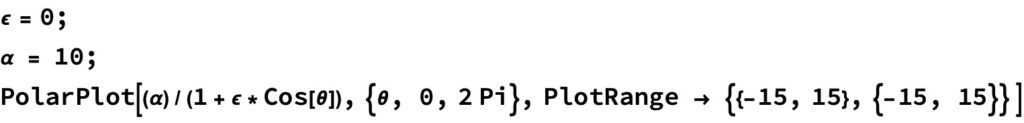
![[그림 1] 궤도 이심률 값이 0이면 원 궤도가 됩니다.](https://ballpen.blog/wp-content/uploads/2024/07/원-1024x1012.jpg)
이와 같이 이심률이 \epsilon =0 의 조건을 만족하면 궤도의 모양은 원이 됩니다.
2. 궤도 이심률이 0보다 크고 1보다 작은 경우 : 타원 궤도
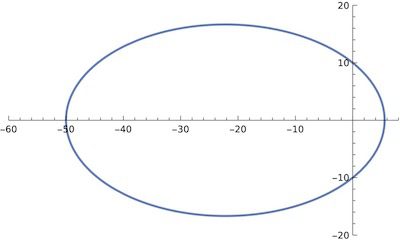
이번에는 (1)식에 이심률 \epsilon = 0.8, \alpha=10을 대입하면 아래 그림과 같이 타원 궤도가 됩니다.
그림을 그리기 위해 사용된 매스매티카 코드는 다음과 같아요.
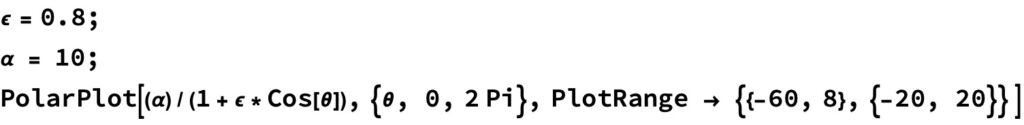
![[그림 2] 궤도 이심률 값이 0보다 크고 1보다 작으면 타원 궤도가 됩니다.](https://ballpen.blog/wp-content/uploads/2024/07/타원-1024x618.jpg)
이와 같이 이심률이 0< \epsilon < 1 의 조건을 만족하면 궤도의 모양은 타원이 됩니다. 이때 이심률이 클수록 타원의 찌그러짐 정도가 커지죠.
참고로 지구 공전궤도의 이심률은 0.0167로서 거의 0과 가까워요. 그래서 원에 가까운 타원궤도를 돌고 있습니다.
3. 궤도 이심률이 1인 경우 : 포물선 궤도
(1)식에 이심률 \epsilon = 1, \alpha=10을 대입하면 아래 그림과 같이 포물선 궤도가 됩니다.
그림을 그리기 위해 사용된 매스매티카 코드는 다음과 같아요.
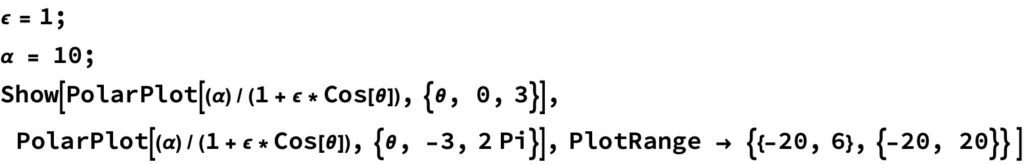
![[그림 3] 궤도 이심률이 1이면 포물선 궤도가 됩니다.](https://ballpen.blog/wp-content/uploads/2024/07/포물선-670x1024.jpg)
이와 같이 이심률이 \epsilon =1 의 조건을 만족하면 궤도의 모양은 포물선이 됩니다.
4. 궤도 이심률이 1보다 큰 경우 : 쌍곡선 궤도
(1)식에 이심률 \epsilon = 1.2, \alpha=10을 대입하면 아래 그림과 같이 쌍곡선 궤도가 됩니다.
그림을 그리기 위해 사용된 매스매티카 코드는 다음과 같아요.
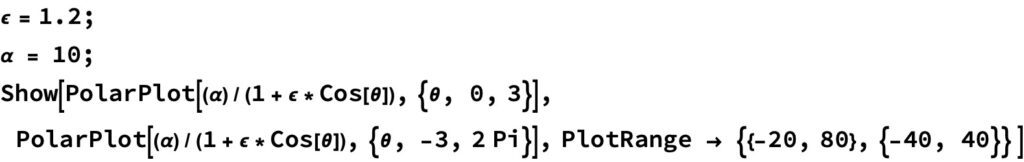
![[그림 4] 궤도 이심률이 1보다 크면 쌍곡선 궤도가 됩니다.](https://ballpen.blog/wp-content/uploads/2024/07/쌍곡선-1024x819.jpg)
이와 같이 이심률이 \epsilon >1 의 조건을 만족하면 궤도의 모양은 쌍곡선이 됩니다.








“궤도 이심률”에 대한 1개의 생각