델 연산자 – 기울기, 발산 , 회전, 라플라시안

Last Updated on 2024-10-26 by BallPen

기울기, 발산, 회전, 라플라시안의 기하학적 의미를 알아봐요.

델 연산자(Del operator)로 스칼라와 벡터장 함수를 미분할 수 있어요. 이때 미분 적용 방식에 따라 기울기, 발산, 회전, 라플라시안의 이름이 붙어있는데요.

예를 들어 전기장의 발산을 구하기 위해서는 전기장에 델 연산자를 내적하고, 회전을 구하기 위해서는 전기장에 델 연산자를 외적합니다.

그런데 궁금한것은 스칼라장과 벡터장에 델 연산자를 취했을 때 기하학적으로 어떻게 상상을 해야 하느냐입니다.

그래서 이번 글에서는 델 연산의 결과를 매스매티카 그래픽으로 설명드릴게요. 그러면 델 연산을 취했을 때 그 결과가 어떠한 모습을 가질지를 상상할 수 있게 됩니다.

참고로 매스매티카로 델 연산을 하기 위해서는 Grad, Div, Curl, Laplacian 명령어를, 그래픽은 Plot3D, VectorPlot, ContourPlot 명령어 등을 사용하면 됩니다.

아래는 이번 글의 목차에요.

1. 스칼라장 함수

일단 설명에 필요한 어떤 스칼라 장(field) 함수를 생각해봐요. 대표적인 스칼라장 함수로는 온도분포가 있어요.

상상을 한번 해보세요.

바닥이 평평한 프라이팬이 있는데요. 팬을 뜨겁게 하기 위해 가스레인지를 켰어요. 그런데 가스레인지가 고장나서 불꽃이 균일하지 않고 어떤 부분은 켜지고 어떤 부분은 꺼져있다고 생각해봐요.

그러면 프라이팬 바닥을 손으로 살짝 만져보면 어떤 부분은 뜨겁고 어떤 부분은 차갑겠죠. 이때 프라이팬 바닥의 좌표 (x, y)에 대응하는 온도 T가 아래의 함수로 주어진다고 생각해보겠습니다.

\tag{1-1}
\begin{align}
T= -2 \cos{(x)}\sin{(y)}
\end{align}

이때 주의 할것은 프라이팬은 물리적으로는 여전히 평평한거에요. 단지 온도 T가 어떤 곳은 뜨겁고 어떤 곳은 차가울 뿐이죠.

그렇다면 (1-1)식을 그래프로 그려보면 어떻게 나타날까요?

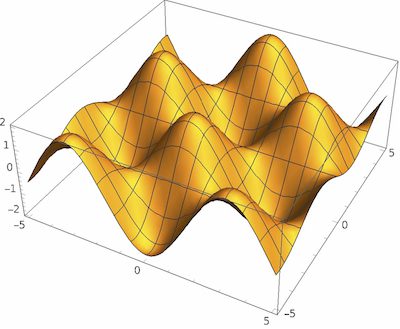
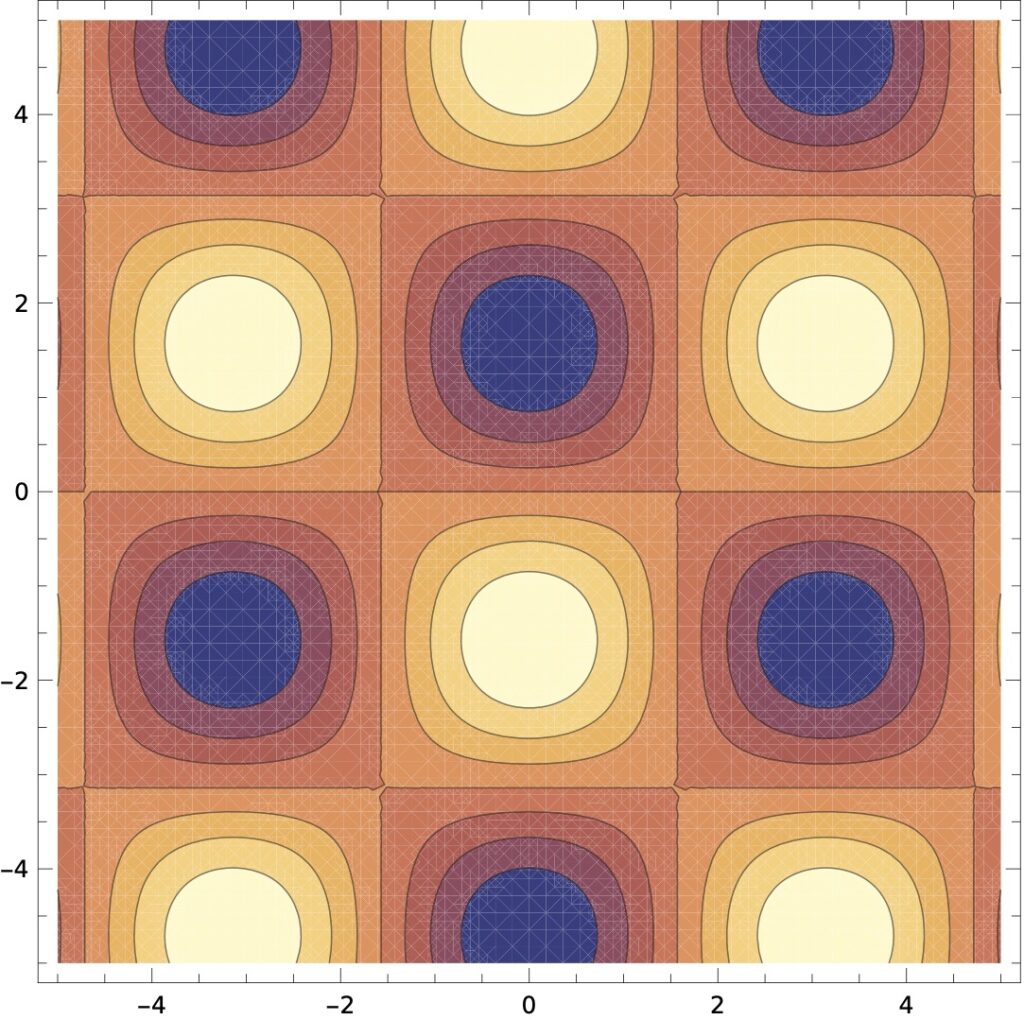
아래 [그림 1]은 Plot3D 명령어로, [그림 2]는 ContourPlot 명령어로 그린 그래픽입니다.

그 결과 [그림 1]처럼 올록 볼록한 모습의 그래픽이 만들어지는데요. 여기서 위로 볼록한 부분이 온도 T가 높아 뜨거운 부분이고 아래로 볼록한 부분은 T가 작아 차가운 부분입니다.

절대로 프라이팬 바닥이 올록 볼록한것이 아님을 꼭 기억하세요.

또한 [그림 2]는 [그림 1]을 위에서 바라본 모습이라고 생각하면 됩니다. 밝은 부분이 온도가 높고 어두운 부분이 온도가 낮아요.

2. 델 연산자

델 연산자(Del Operator)는 기호로 나블라 \nabla를 사용하는데요. 수학적으로는 미분을 수행하는 연산자일 뿐이에요. 매번 미분식을 길게 쓰자니 불편해서 간결하게 기호로 표현한 거에요.

델 연산자는 다음 식과 같이 정의됩니다.

\tag{2-1}
\nabla = \Big({{\partial}\over{\partial x}}\hat x + {{\partial}\over{\partial y}}\hat y + {{\partial}\over{\partial z}}\hat z \Big)

이 연산자에 스칼라장 함수를 적용하면 기울기(그래디언트, gradient)라 하고 벡터장 함수를 내적하면 발산(다이버전스, divergence), 외적하면 회전(컬, curl)이라 합니다. 또한 스칼라장의 기울기에 발산을 취한 것을 라플라시안(Laplacian)이라고 하죠.

각각의 기하학적 의미를 계속 알아볼께요.

3. 델 연산자 : 기울기, 발산, 회전, 라플라시안

3-1. 기울기(그래디언트, gradient)

(1-1)식의 스칼라함수에 (2-1)식의 델 연산자를 작용하면 기울기 연산이 됩니다. 구체적인 풀이 과정은 아래 (3-1)식과 같아요.

\tag{3-1}
\begin{align}
\nabla T &= \Big({{\partial}\over{\partial x}}\hat x + {{\partial}\over{\partial y}}\hat y + {{\partial}\over{\partial z}}\hat z \Big) \Big(-2 \cos{(x)}\sin{(y)}\Big)\\[10pt]
&= 2 \sin x \sin y \hat x -2\cos x \cos y\hat y
\end{align}

스칼라장에 기울기를 취하면 벡터함수가 나오는 것을 알 수 있어요.

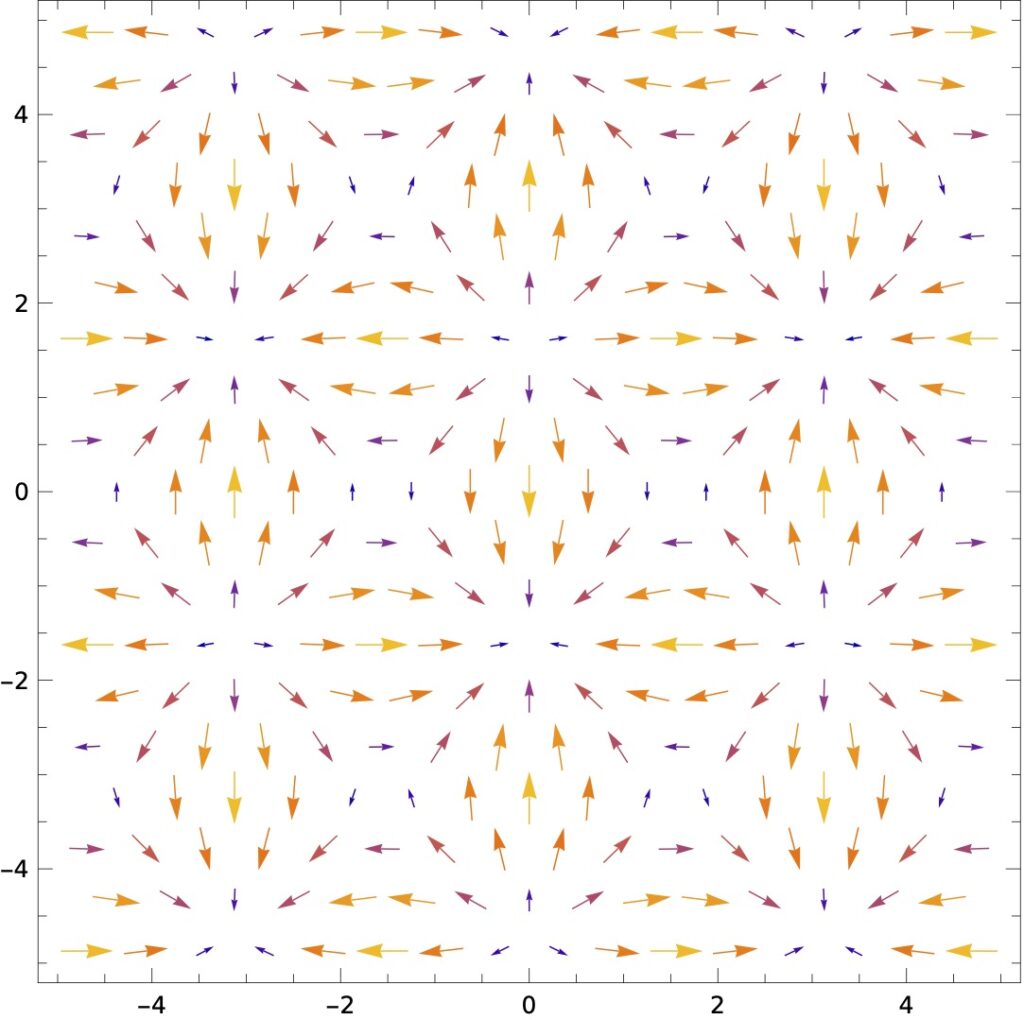
그러면 (3-1)식의 벡터함수 \nabla T를 매스매티카의 VectorPlot 명령어로 그려보면 어떤 모양이 만들어질까요? 그 결과가 [그림 3]입니다. 참고로 기울기 연산의 전과 후를 비교하기 위해 [그림 2]를 함께 나타냈어요.

두 그림을 비교해보세요.

기울기 연산을 취한 다는 것은 스칼라 함수값이 낮은 곳에서 높은 곳을 향하는 벡터를 각 위치마다 구하는 것과 같다는 것을 알 수 있어요. 엄밀히 말하면 [그림 2]의 등고선에 수직한 벡터인데요. 그 방향은 스칼라장 값이 작은 쪽에서 큰 쪽을 향하는 거죠.

물론 온도 변화가 큰 부분은 벡터 화살표의 길이가 길고, 온도 변화가 작은 부분은 벡터 화살표의 길이가 짧아요.

그러다 보니 온도가 낮은 부분은 마치 물이 샘솟는 것처럼(양의 발산) 벡터장이 표현되고, 온도가 높은 부분은 물이 구멍으로 빠져나가는 것처럼(음의 발산) 표현됨을 알 수 있어요.

3-2. 발산(다이버전스, divergence)

이번에는 벡터장에 델 연산자를 내적하는 발산을 알아볼게요.

이를 위해서는 벡터장 함수가 필요한데요.

편의상 우리가 이미 만들어 놓은 (3-1)식의 \nabla T를 벡터장 \vec K로 치환하여 활용하겠습니다. 이때 벡터장 \vec K를 스칼라장의 기울기로부터 구했다고 연계해서 생각하지 마시고. 그냥 임의로 주어진 벡터장이라고 생각하시기 바랍니다.

구체적인 발산 풀이 과정은 아래와 같아요.

\tag{3-2}
\begin{align}
\nabla \cdot \vec K &= \Big( {{\partial}\over{\partial x}}\hat x + {{\partial}\over{\partial y}} \hat y + {{\partial}\over{\partial z}}\hat z   \Big) \cdot\Big(2 \sin x \sin y \hat x - 2 \cos x \cos y \hat y    \Big)\\[10pt]
&=2 \cos x \sin y + 2 \cos x \sin y \\[10pt]
&=4 \cos x \sin y
\end{align}

벡터장에 발산을 취하면 스칼라장이 나온다는 것을 알 수 있어요.

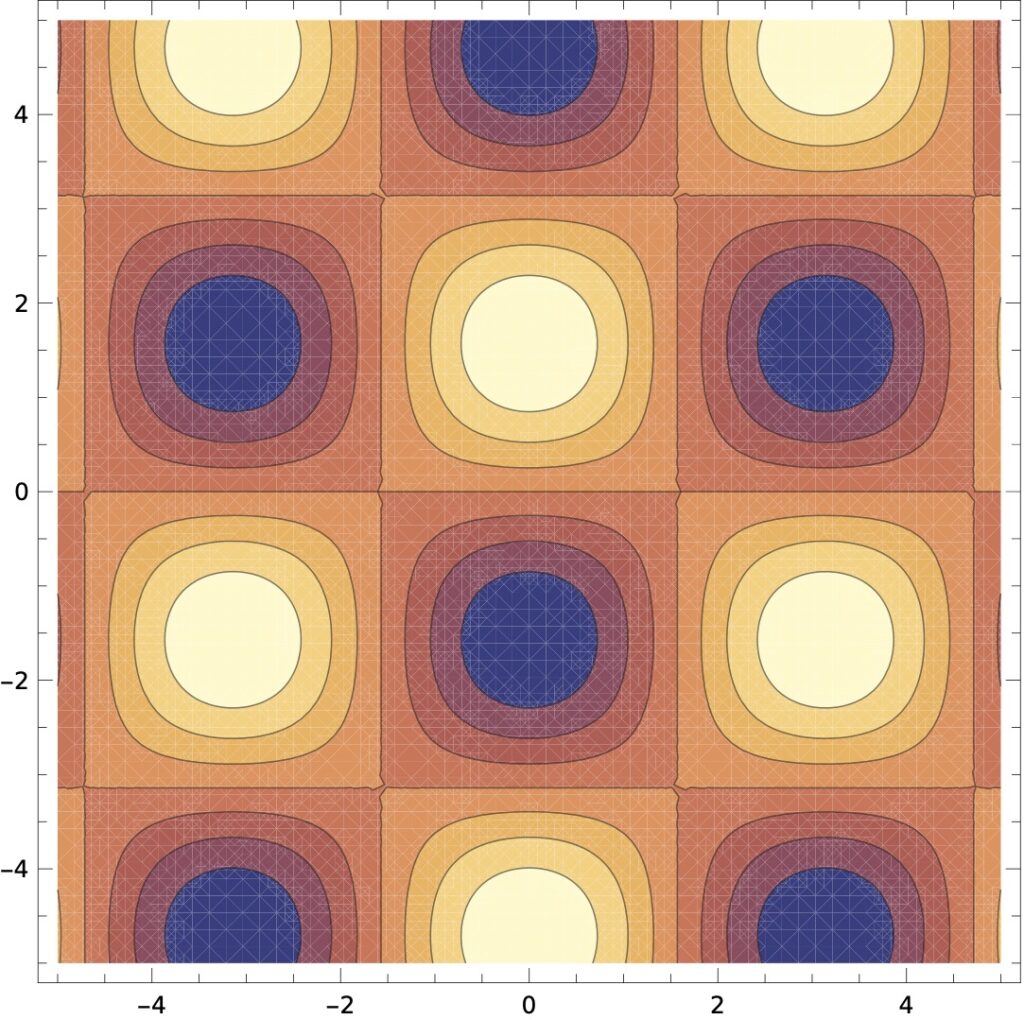
그렇다면 (3-2)식 스칼라장의 모양은 어떨까요? 그것을 그림으로 그린 것이 아래 [그림 4]입니다. 참고로 발산 연산의 전과 후를 비교하기 위해 [그림 3]을 함께 나타냈어요.

그 결과 어떤 벡터장의 발산을 연산한다는 것은, 벡터장들이 샘솟는 곳은 밝게(양의 발산), 벡터장들이 빠져나가는 곳은 어둡게(음의 발산) 표현되는 스칼라장이 된다는 것을 알 수 있을거에요.

그러므로 만일 벡터장이 [그림 3]처럼 샘솟거나 사라지는 부분없이 특정 방향을 향하는 상수벡터들로만 이루어졌다면 벡터장의 발산은 [그림 4]처럼 올록 볼록하지 않고 단순한 평면(상수벡터를 미분하면 0이 되므로)으로 나타나게 됩니다.

3-3. 회전(Curl)

이번에는 벡터장에 델 연산자를 외적하는 회전을 알아보겠습니다. 이를 위해서는 벡터장이 필요한데요.

아래 식으로 주어진 어느 벡터장 \vec V을 활용하겠습니다.

\tag{3-3}
\vec V = y \hat x - x \hat y

이 벡터장에 델 연산자를 외적하면 회전을 구할 수 있어요. 구체적인 계산 방법은 다음과 같습니다.

\tag{3-4}
\begin{align}
\nabla \times \vec V &= 

   \begin{vmatrix} 
   \hat x & \hat y & \hat z  \\
   {{\partial}\over{\partial x}} & {{\partial}\over{\partial y}} & {{\partial}\over{\partial z}}  \\
   y & -x & 0  \\
   \end{vmatrix} \\[10pt]

&=\Big ( {{\partial}\over{\partial y}}0-{{\partial}\over{\partial z}}(-x) \Big)\hat x + \Big({{\partial}\over{\partial z}}y -{{\partial}\over{\partial x}}0 \Big) \hat y+\Big({{\partial}\over{\partial x}}(-x) - {{\partial}\over{\partial y}}y \Big) \hat z\\[10pt]
&=(0-0)\hat x + (0 - 0)\hat y + (-1-1)\hat z\\[10pt]
&=-2 \hat z
\end{align}

그럼 이번에도 회전을 취하기 전의 벡터장 (3-3)식과 회전을 취한 후의 벡터장 (3-4)식을 함께 그려 비교해 볼게요. 그 결과는 아래와 같습니다.

위 그림들에서 [그림 5]는 회전 연산 전 (3-3)식의 벡터장을 3차원으로 나타낸 그림인데요. 아무래도 화살표가 많아 전체를 이해하기 쉽지 않아요.

그래서 z=0 평면에서만 그려본것이 [그림 6]입니다. 뱅글 뱅글 회전하는 벡터들을 볼 수 있어요. 저런 벡터들이 위 아래로 층층이 쌓여 있는 것이 [그림 5]가 되는거에요.

회전을 취한 후의 결과는 [그림 7]입니다. 위에서 아래 방향으로 모두 동일한 크기와 방향을 갖는 상수벡터들이 만들어졌음을 알 수 있어요.

즉 어느 벡터장에 회전을 취한다고 하는 것은, 오른손법칙에 따라 손가락 4개를 벡터장의 회전 방향을 향하게 하고 엄지손가락을 폈을 때 향하는 벡터들을 그려내는 거에요. 물론 [그림 6]의 회전 방향이 반대가 된다면 [그림 7]의 벡터장은 위쪽을 향하게 됩니다.

그렇다면 [그림 3]의 벡터장에 회전을 취하면 어떻게 될까요? 네. 그때는 0이 될거에요. 왜냐면 [그림 3]의 벡터장은 수렴과 발산만 있을 뿐 회전하는 요소가 하나도 없기 때문이죠.

3-4. 라플라시안(Laplacian)

라플라시안은 어떤 스칼라장 T에 대한 기울기의 발산을 말해요. 식으로 쓰면 다음과 같습니다.

\tag{3-5}
\begin{align}
\nabla \cdot (\nabla T) = \nabla^2 T = {{\partial^2 T}\over{\partial x^2}} + {{\partial^2 T}\over{\partial y^2}} + {{\partial^2 T}\over{\partial z^2}}
\end{align}

그럼 (1-1)식의 스칼라장에 라플라시안을 구해볼께요. 그 결과는 아래와 같습니다.

\tag{3-6}
\begin{align}
\nabla^2 T &= 2 \cos x \sin y + 2 \cos x \sin y + 0\\
&=4 \cos x \sin y
\end{align}

그럼 스칼라장에 라플라시안 연산 전과 후의 모습은 어떻게 될까요? 이것에 대해서는 이미 앞에서 모두 끝냈습니다.

즉 [그림 2]가 스칼라장 T, [그림 4]는 T에 기울기의 발산을 구한 결과이므로 라플라시안 연산 후의 스칼라장이 되는 것이죠.

라플라시안을 적용한 후인 [그림 4]에서 밝고 어두운 부분이 생성되는 이유는 [그림 2]의 최초 스칼라장에서 올록 볼록한 부분이 있었기 때문이에요.

그래서 우리가 알지 못하는 어떤 스칼라장에 라플라시안을 취했더니 0이 나왔다면 최초의 스칼라장은 올록 볼록한 것이 아니라 평평한 구조를 갖고 있었음을 알 수 있게 되는 거죠. 물론 평평한 상태에서 기울어져 있어도 라플라시안을 취하면 0이 됩니다.

Related posts.

자동차 사양서 – 토크, 등급, CO2, 정부 공인 표준 연비 등의 제원 설명 자동차 배기량(displacement)의 정의와 어떻게 계산하는지를 알아볼까요? 자동차의 최고출력 개념과 이 값이 크면 무엇이 좋은가? 인공지능 기술 분야. 중소기업은 머신러닝 중심, 그럼 대기업은? 밀도 정의와 활용 사례 단위 표기 오류가 있는 도쿄 올림픽 중계방송이 불편한 이유 등가소음도 계산 방법 알려 드립니다. 음압레벨도 함께 공부해요. 선풍기 살 때 풍량 효율 큰 것 고르면 되는 거에요?