Last Updated on 2025-09-07 by BallPen
속력과 속도를 구분하는 이유와 두 개념 사이의 차이를 사용 사례를 들어 소개합니다.
속력과 속도에 대한 이야기를 이번 글에서 다루고자 합니다.
속력(speed)과 속도(velocity)의 공식을 알고 있는 사람은 많이 있습니다. 그러나 두 개념을 구분해서 공부하는 이유와 언제 속력과 속도를 적용하고 사용해야 하는지를 모르는 경우가 많습니다.
서로 비슷하면서도 다른 속력과 속도를 알아볼까요? 아래는 이번 글의 목차입니다.
Contents
혹시 가속도에 관한 내용이 궁금한 사람은 아래의 글을 참고해 주세요.
- 가속도-빠르게 움직이면 가속도가 큰거에요? (클릭)
1. 이동거리와 변위
속력과 속도를 구분하기 위해서는 우선 이동거리(distance)와 변위(displacement)에 대한 내용을 알아야 합니다.
![[그림 1] 속력과 속도 개념을 알기 위해서는 이동거리와 변위의 차이를 우선 구분해야 합니다. 어느 물체가 처음 위치에서 나중 위치로 움직였을 때, 이동거리는 물체가 이동한 실제 경로의 총 길이이고, 변위는 나중위치와 처음위치 사이의 직선거리를 뜻합니다.](https://ballpen.blog/wp-content/uploads/2021/08/Picture1-2-1024x446.png)
어느 물체가 [그림 1]과 같이 파랑색 경로를 따라 처음 위치에서 나중 위치로 움직여갔다고 생각해 보세요.
이때 이동거리란 실제 물체가 이동한 경로상의 총 거리를 뜻합니다. 그러므로 [그림 1]에서 이동거리는 파랑색 경로의 전체 길이인 520 m가 되는 것입니다. 물론 나중 위치까지 이동하는 경로가 구불구불 할수록 이동거리는 늘어나겠죠.
이에 비해 변위의 크기는 나중과 처음 위치 사이의 직선 거리를 뜻합니다. 즉 [그림 1]과 같이 나중 위치와 처음 위치 사이의 거리가 270 m라면 바로 변위의 크기가 270 m임을 의미합니다. 그러므로 변위는 실제 이동하는 경로가 구불구불 할지라도 처음과 나중위치만 같으면 동일한 값을 갖게 됩니다.
이동거리와 변위사이의 또 다른 특징은 이동거리는 크기만 갖는 스칼라이고 변위는 크기와 방향을 갖는 벡터입니다. 따라서 변위를 표기할 때에는 크기 뿐만 아니라 방향 표기도 빠트리면 안됩니다.
– 관련 예제 풀이
(예제1) 가로방향으로 반듯한 직선도로에서 자전거를 타는 사람이 있다. 이 도로를 따라 170 m를 오른쪽으로 가다가 뒤로 돌아 왼쪽으로 56 m를 가고, 다시 뒤로 돌아 오른쪽으로 30 m를 갔다. 이동거리와 변위는 각각 얼마인가?
(Sol) 이동거리는 자전거가 도로를 따라 실제 이동한 경로의 총 합입니다. 그러므로 이동거리 d는 아래 (1)식과 같이 256 m입니다.
\tag{1}
\begin{aligned}
d &= 총 ~이동~거리\\[10pt]
&= 170 ~\mathrm{m} + 56~\mathrm{m} + 30 ~\mathrm{m}\\[10pt]
&=256~ \mathrm{m}
\end{aligned}변위는 어떻게 될까요? 변위의 크기는 나중 위치와 처음 위치 사이의 직선거리입니다. 그러므로 변위 \vec{d}는 다음 (2)식과 같습니다.
\tag{2}
\begin{aligned}
\vec{d} &= 오른쪽~170 ~\mathrm{m}+(왼쪽~-56~\mathrm{m}) + 오른쪽 ~30 ~\mathrm{m}\\[10pt]
&= 오른쪽~144~\mathrm{m}
\end{aligned}즉, 변위는 오른쪽 방향으로 144 m입니다. 이 표현에서 ‘오른쪽’이 변위의 방향이고 ‘144’는 변위의 크기입니다.
2. 속력과 속도
2-1. 속력과 속도 개념 차이
속력과 속도 개념은 물리학에서 역학의 초기 부분에 등장합니다. 이 둘은 공식도 비슷하고 개념도 비슷해서 많이 헷갈려요.
우선 속력과 속도는 \mathrm{m/s}로 단위가 동일하지만 서로 다른 물리적 의미를 갖습니다. 아래 표는 그 내용을 정리한거에요.
| 구분 | 속력 | 속도 |
|---|---|---|
| 1 | 단위시간당 물체의 총 이동거리(distance) | 단위시간당 물체의 총 변위(displacement) |
| 2 | 크기만 있고 방향이 없는 스칼라량 | 크기 뿐만 아니라 방향도 있는 벡터량 |
| 3 | 이동하는 물체의 평균 속력은 절대로 0이 될 수 없음 | 이동하는 물체의 평균 속도는 변위가 0일때 0이 될 수 있음 |
| 4 | 이동하는 물체의 빠르기에 대한 정보를 줌 | 이동하는 물체의 빠르기와 방향에 대한 정도를 줌 |
| 5 | 움직이는 물체의 속력은 음수가 될 수 없음 | 움직이는 물체의 속도는 음수, 양수, 0도 될 수 있음 |
2-2. 속력과 속도 공식
속력 s는 전체 이동거리 d를 경과시간 t로 나눈 값입니다.
\tag{3}
\begin{align}
s &= {{d}\over{t}}
\end{align}이와 달리 속도 \vec {v}는 변위 \vec {d}를 경과시간 t로 나눈 값입니다.
\tag{4}
\begin{align}
\vec{v} = {{\vec{d}}\over{t}}
\end{align}(3)식과 (4)식에서와 같이 이동거리를 사용하느냐 변위를 사용하느냐에 따라 속력과 속도의 공식은 달라집니다. 다만 두 식의 분자에 있는 이동거리와 변위의 단위가 모두 m이므로 속력과 속도의 단위는 m/s로 동일합니다.
– 관련 예제 풀이
(예제2) [그림 1]에 주어진 상황을 이용하여 속력과 속도를 구하여라. 이때 경과 시간 t는 480 s로 계산하고 물체는 수평면에 대해 30^\circ로 방향으로 이동한다.
(Sol) [그림 1]에서 이동거리 d는 520 m입니다. 그러므로 속력을 구하면 아래 (5)식과 같이 1.08 m/s가 나옵니다. 즉 물체는 1초당 1.08 m를 가는 빠르기로 이동한 것입니다.
\tag{5}
\begin{aligned}
s &= {{d}\over{t}}\\[10pt]
&={{520 ~\mathrm{m}}\over{480~{\mathrm{s}}}}\\[10pt]
&=1.08~\mathrm{m/s}
\end{aligned}이번에는 속도를 구해보겠습니다. [그림 1]에서 변위의 크기 \vec d는 270 m입니다. 이를 바탕으로 속도를 구하며 아래 (6)식과 같이 속도의 크기는 0.56 m/s이고, 방향은 변위의 방향과 동일한 수평면으로부터 30^\circ방향입니다.
\tag{6}
\begin{aligned}
\vec{v} &= {{\vec{d}}\over{t}}\\[10pt]
&={{270 ~\mathrm{m}}\over{480~\mathrm{s}}}\\[10pt]
&=0.56~ \mathrm{m/s} ~(수평면으로부터~30^\circ~ 방향)
\end{aligned}3. 속력과 속도 : 사용 사례
그렇다면 어느 물리적 상황에서 속력과 속도가 사용될까요?
3-1. 속력을 사용하는 예
[그림 2]와 같이 어느 자동차가 주차장을 출발하여 20 min 동안 12 km인 동네 한바퀴를 돌고 다시 출발했던 주차장으로 되돌아 온 경우를 생각해 보겠습니다.
![[그림 2] 자동차가 처음 위치를 출발하여 12 km 길이의 동네를 한바퀴 돌고 다시 처음 위치로 돌아왔습니다. 그러면 이동거리는 12 km이고, 변위는 0 m가 됩니다.](https://ballpen.blog/wp-content/uploads/2021/08/Picture2-2-1024x508.png)
그런데 누군가가 자동차가 주행하는 동안 휘발유 1.0 L가 소모되었으니, 주행 빠르기가 얼마였냐고 묻는다면 여러분들은 속력이나 속도 중 무엇으로 답하겠습니까?
당연히 속력으로 답할거에요. 속력을 구하면 아래 (7)식과 같이 10 m/s가 나옵니다.
\tag{7}
\begin{aligned}
s &= {{d}\over{t}}\\[10pt]
&={{12~\mathrm{km} \times(1,000~\mathrm{m}/1~\mathrm{km})}\over{20~\mathrm{min} \times({60~\mathrm{s}/1~\mathrm{min})}}}\\[10pt]
&={{12,000~\mathrm{m}}\over{1,200~\mathrm{s}}}\\[10pt]
&=10~\mathrm{m/s}
\end{aligned}그렇다면 (4)식을 이용하여 속도를 구하면 어떨까요? 그런데 변위가 [그림 2]에서와 같이 0 m입니다. 그러므로 속도의 크기가 0 m/s가 되어버리는 군요.
만약 “속도가 0 m/s 였습니다”라고 답한다면 질문을 한사람은 차가 주행하지 않았다는 것으로 오해하고 황당해 할 수 있어요. 왜 그러냐면 일반 사람들은 속력과 속도를 엄밀하기 구분해서 사용하지 않기 때문입니다.
이와 같이 단순히 어느 물체의 빠르기 정보만이 필요한 경우에는 속도보다는 속력을 사용해야 합니다.
속력을 사용해야 하는 유사한 사례로는 다음과 같은 것들이 있습니다.
- 지그재그로 움직이는 어느 물체의 순간적인 빠르기 정보를 표현하고 싶을 때
- 어느 위치에서 강에 흐르는 물의 유속을 표현하고 싶을 때
3-2. 속도를 사용하는 예
이런 경우를 생각해보세요.
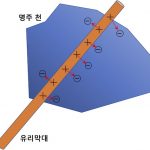
![[그림 3] 공기중에 있는 향수 분자의 속력은 수백 m/s로 매우 빨라 단위시간 동안 이동한 거리는 매우 큽니다. 그러나 이동과정 중 공기 분자와의 수많은 충돌로 지그재그로 이동하게되어 향수병으로부터 주변으로 퍼져나간 변위는 그렇게 크지 않습니다.](https://ballpen.blog/wp-content/uploads/2021/08/Picture3-1-1024x599.png)
[그림 3]과 같이 방의 중간에 향수 병이 있습니다.
만약 향수 병을 누군가가 열어 놓았다면 그 냄새가 주변으로 퍼져 나갈거에요. 이때 병 밖으로 방출된 개별 향수 분자의 속력은 보통 수백 m/s 정도로 매우 빠릅니다.
그러나 실제로는 향수 냄새가 그렇게 빨리 퍼져나가지는 않는다는 것을 경험상 알고 있어요. 향수병이 열리고 거리에 따라 다르겠지만 몇 초 정도 걸려야 방안 저 끝까지 향수냄새가 전달되니까요.
그렇다면 향수 분자의 속력은 수백 m/s로 빠른데 냄새가 퍼지는 확산속도는 왜 그렇게 크지 못할까요? 그 이유는 향수분자가 주변으로 이동할 때 공기분자와 수많이 충돌하여 분자는 지그재그로 움직이게 됩니다.
따라서 단위시간당 분자의 전체 이동거리([그림 3]에서 구불구불한 경로에 대한 전체 길이)는 매우 크지만 향수병으로부터 향기 분자가 퍼져나간 실제 변위는 매우 작습니다.
자 그렇다면 향수냄새의 확산 빠르기는 속력과 속도중 무엇으로 표현해야 할까요? 바로 속도로 해야 합니다.
예를 들어, 위의 그림처럼 향수병이 있는 위치로부터 바깥방향으로 10.0 m 떨어진 지점까지 냄새가 확산하는데 37.0 s 걸렸다면 속도는 얼마일까요? 바로 아래 (8)식에서와 같이 0.270 m/s가 나옵니다.
\tag{8}
\begin{aligned}
\vec{v} &= {{\vec{d}}\over{t}}\\[10pt]
&= {{10.0~\mathrm{m}}\over{37.0~\mathrm{s}}}\\[10pt]
&=0.270~\mathrm{m/s}~~(병으로부터~ 멀어지는~ 방향)
\end{aligned}속도를 사용해야 하는 유사한 사례로는 다음과 같은 것들이 있습니다.
- 어느 댐이 파괴되어 강을 따라 물이 퍼져나가고 있습니다. 댐으로부터 남쪽 방향으로 직선거리 30.0 km 떨어진 어느 도시까지 물이 전달되는 정보를 시민들에게 제공하고자 한다면 속도 표현을 사용하는게 좋습니다. 예를 들어 남쪽 도시로 전달되는 물의 속도가 15.0 km/h라고 한다면 사람들은 2시간이면 도시에 홍수가 발생할 것을 알고 미리 대피할 수 있기 때문입니다. 그런데 만일 속도가 아닌 속력정보를 알려주게 되면 강의 구불구불한 전체 이동경로를 아는 사람이 많지 않기 때문에 도시로 물이 도착하는 경과시간을 정확하게 구하지 못해 불필요한 혼란을 주게 됩니다.
- 도선내에 전류가 흐를때 전자의 이동을 속도로 표현합니다. 이것은 향수냄새의 경우와 비슷한데요. 도선내에서 순간적인 전자의 이동 속력은 매우 빠를 수 있습니다. 그러나 이동과정 중 원자와의 수많은 충돌로 단위시간당 전자의 실제 변위는 생각보다 매우 작습니다.
4. 속력과 속도에 대한 내용 요약
- 속력과 속도의 단위는 \mathrm{m/s}로 같다. 그러나 속력은 이동거리를 경과시간으로 나누고 속도는 변위를 경과시간으로 나눈다.
- 그러므로 속력은 어느 시간동안 이동 경로 상의 빠르기에 대한 정보를 표현하는데 유용하다. 이와 달리 속도는 이동 경로보다는 나중과 처음위치 사이의 빠르기와 방향 정보를 표현하는데 유용하다.
- 속력이 실생활에서 주로 사용되지만 속도가 사용되어야 하는 다양한 사례도 많다.


안녀하세요?
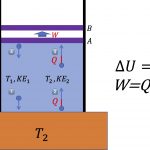
소형 원심분리기의 kinetic energy 룰 구하려고 합니다.
로터의 지름은 90mm , RPM은 6,000rpm 입니다.
로터의 무게는 32g 입니다.
kinetic energy (J)를 구하기 위해 필요한 정보가 있는지요?
댓글을 이제서야 확인했어요.
답장이 늦어 미안합니다.
사실 제가 원심분리기를 사용해본 적이 없어 구조를 잘 몰라요.
다만 회전운동에너지를 구하기 위해서는 W=(1/2)Iw^2으로 구할 수 있어요.
RPM이 주어져 있으니 각속력 w는 구할 수 있는데요. 문제는 로터의 관성모멘트 I를 계산하거나 측정해야 해요.
관성모멘트는 질량 m뿐만 아니라 회전축으로부터 질량이 있는 곳까지의 거리 r에 따라서도 달라져요.
즉 질량이 동일한 물체일지라도 모양이 어떻게 생겼느냐에 따라 관성모멘트는 서로 다른 값을 갖습니다.
로터가 대칭인 구조라면 관성모멘트 I를 근사적으로 계산 할 수도 있겠지만 복잡한 구조라면 측정이 더 편할거에요.
정리하면 로터의 관성모멘트 I를 구한 후 위 공식에 대입하면 됩니다.
큰 도움 못드려 죄송합니다.
안녕하세요.
글 감사히 잘 보고갑니다.
궁금한것들을 잘 찾아보고 있습니다.
항상 건강하시고 행복하세요.
방문해주시고 관심가져주셔서 감사합니다.
글 감사히 잘보고있습니다. 혹시 출처를 남기고 퍼가도될까요?
방문해 주셔서 감사합니다. 출처 남기시고 퍼가셔도 됩니다.
변위가 0이되면 속도가 0 이되게 되는데 그럼 운동을 안했다고 봐야 하나요? 운동의 정의는 다를까요?
쿠쿠리님 방문해주셔서 감사합니다.
속도는 주어진 시간 동안의 변위로 정의됩니다. 그래서 주어진 시간 동안 변위가 0이면 물체의 평균속도는 0이되고, 주어진 시간 동안 운동을 전혀 하지 않은 것으로 간주됩니다.
예를 들어 엄마가 아이에게 공부하라고 말하고 책상에 강제로 앉혔어요. 그리고는 1시간 후에 아이가 공부하는지 잠시 문을 열어봤는데 아이가 책상에 앉아 공부하고 있으면 엄마는 아이가 1시간 동안 움직이지 않고 공부를 계속 하고 있는 것으로 생각하게 되는 것과 같아요. 만일 엄마가 1시간 후에 공부하는지 문을 여는 것을 아이가 미리 알고 엄마가 문을 열어볼 때를 제외하고는 침대에서 휴대폰 보고 딩굴딩굴 놀았을지라도 엄마는 그러한 사실을 전혀 알 수 없습니다.
아마도 쿠쿠리님이 질문하신 의도는 주어진 시간 동안 어느 물체의 변위가 0이면 속도가 0이 되는데, 주어진 시간 사이에 물체가 운동했다면 변위가 있었을 것이고 그렇다면 이때 속도는 어떻게 되느냐의 내용인 것 같아요. 만일 주어진 시간 사이에 물체가 움직였고 그때의 속도를 구하고 싶다면 주어진 시간의 크기를 작게하면 됩니다. 즉 더 촘촘하게 측정을 하면 되는 거에요. 1초마다 변위를 측정하던 것을 0.5초마다 측정하면 더 촘촘하게 속도를 구할 수 있게 됩니다. 그러면 1초마다 제자리로 돌아와 변위가 0이되는 물체일지라도 0.5초 마다의 변위와 속도를 구할 수 있게 되요.
예를 들어 아이가 공부하는지를 엄마가 더 상세하게 알고 싶다면 1시간마다 문을 열어보는 것이 아니라 30분마다 문을 열어보면 공부를 계속 잘 하고 있는지의 여부를 더 잘 알 수 있잖아요.
사실 과학에서는 측정을 더 촘촘하게 하기 위해 많은 노력을 하고 있어요. 그래야 더 짧은 시간동안의 운동 상태를 알 수 있게 되니까요.
답변 감사합니다. 다시 보니 질문을 너무 줄여서 쓰긴 했네요
답변 주신대로 전체 시간에 대한 변위는 0 이라도 중간에는 이동을 했는데 운동을 안했다고 봐야 하는지 궁금했습니다.
예전부터 궁금해 하던 정의였는데 쉽게 이해할 수 있게 설명해 주셔서 감사합니다.^^
조영미님 방문해 주셔서 감사합니다.^^
잘 보고 갑니다
방문해 주셔서 감사합니다.^^