Last Updated on 2025-08-23 by BallPen
입자의 궤도방정식에 역제곱 중심력을 대입하면 타원궤도가 얻어짐을 알아 봐요.
케플러 제1법칙(Kepler’s 1st law of planetary motion)이란 태양을 한 초점으로 하는 타워궤도를 따라 행성이 공전한다는 법칙입니다.
따라서 이 법칙을 타원궤도의 법칙이라고도 불러요.
이 법칙은 입자의 궤도방정식에 역제곱 중심력을 대입하여 공전각도 \(\theta\)에 따른 입자의 궤도식을 구함으로써 명확이 입증할 수 있습니다. 그 결과는 다음 식으로 주어져요.
\begin{align}
\tag{D1}
r = {{ml^2 /k}\over{1+(A ml^2 /k ) \cos \theta}}
\end{align}
여기서 \(r\)은 태양으로부터 행성까지의 거리, \(m\)은 행성의 질량, \(l\)은 단위질량당 각운동량, \(k=GMm\)으로서 만유인력상수와 태양 질량과 행성 질량을 곱한 양입니다. \(A\)는 행성에 따른 상수이고, \(\theta\)는 공전각도를 의미해요.
위 (D1)식을 컴퓨터로 그려보면 실제 타원궤도가 나오는 것을 알 수 있어요. 이제부터 (D1)식이 어떻게 유도되는지 알아보고 그 의미를 살펴봐요.
아래는 이번 글의 목차입니다.
Contents
1. (복습) 중심력에서 입자의 궤도 방정식
뉴턴운동의 제2법칙에 중심력을 적용하면 입자의 궤도 방정식을 도출할 수 있습니다. 궤도 방정식은 미분방정식으로 나타나는데 다음과 같아요.
\begin{align}
\tag{1-1}
{{d^2 u}\over{d \theta^2}} + u = – {1 \over {ml^2 u^2}} f(u^{-1})
\end{align}
여기서 \(u\)는 다음의 관계를 가집니다.
\begin{align}
\tag{1-2}
u = {1 \over r}
\end{align}
(1-1)식에 역제곱 중심력을 대입한 후 미분방정식을 풀면 \(r(\theta)\) 식을 얻을 수 있게 됩니다. 이에 대해 계속 알아 봐요.
2. 입자의 궤도 방정식 풀이
2-1. 중심력과 역제곱 중심력(역제곱 법칙)
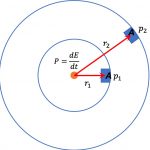
중심력이란 물체의 지름방향을 따라 떨어진 거리에 의존하는 힘을 의미합니다.
예를 들어 태양과 지구 사이의 만유인력은 두 입자의 중심을 연결한 직선 상의 떨어진 거리 \(r\)에 의존하여 힘이 작용하므로 대표적인 중심력입니다. 식으로 쓰면 다음과 같아요.
\begin{align}
\tag{2-1}
F = -{{GMm}\over{r^2}}
\end{align}
여기서 음의 부호는 두 입자 사이에 인력이 작용하기 때문에 붙인 거에요. 또한 \(M\)은 태양의 질량, \(m\)은 지구의 질량이에요.
여기서 중요한 것은 작용하는 힘 \(F\)가 태양과 지구사이의 떨어진 거리 \(r\)에 의존하는 중심력인데, 그 중에서도 특히 \(r^2\)에 반비례한다는 거에요. 즉, 아래 (2-2)식의 관계가 성립해요.
\begin{align}
\tag{2-2}
F \propto {1 \over r^2}
\end{align}
이러한 유형의 힘을 역제곱 중심력이라고 불러요. 역제곱 중심력은 만유인력 뿐만 아니라 두 전하사이의 전기력 등에서도 나타납니다.
따라서 역제곱에 비례하는 물리량들을 통칭하여 역제곱 법칙(inverse square law)이라고 말하기도 합니다.
2-2. 입자의 궤도 방정식에 역제곱 중심력 대입
이제 (1-1)식의 궤도방정식에 (2-1)식으로 주어지는 만유인력, 즉 역제곱 중심력을 대입해 봐요. 이 중심력을 대입하는 이유는 태양과 행성 사이에 작용하는 힘이 만유인력 뿐이기 때문이에요.
그런데 (2-1)식의 만유인력 공식에서 분자의 \(GMm\)은 상수끼리의 곱이므로 상수가 될 뿐이이에요. 그래서 매번 이것을 복잡하게 쓰는 것 보다 \(k\)라고 치환해서 간단히 표현하도록 하겠습니다.
따라서 (2-1)식의 만유인력은 다음과 같이 표현할 수 있어요.
\begin{align}
\tag{2-3}
F = – {k \over r^2}
\end{align}
위 (2-3)식을 (1-1)식에 대입하면 다음과 같아요. 이때 (1-2)식의 관계도 적용했어요.
\begin{align}
\tag{2-4}
{{d^2 \theta}\over{d \theta^2}} + u = – {1 \over{ml^2 u^2}}(-ku^2)
\end{align}
그리고 윗 식을 한번 더 정리하면 다음과 같습니다.
\begin{align}
\tag{2-5}
{{d^2 u}\over{d \theta^2}} + u = {{k}\over{ml^2}}
\end{align}
[미분방정식의 일반해 구하기]
(2-5)식은 비제차 이계 선형 상미분방정식으로 보조해와 특성해의 결합으로 주어지는 일반해를 갖습니다. 식으로 쓰면 다음과 같아요.
\begin{align}
\tag{2-6}
u = u_h + u_p
\end{align}
여기서 \(u_h\)는 보조해로서 (2-5)식의 우변을 0으로 두고 푼 해로, 단순조화진동자의 운동방정식과 같은 형태임을 알 수 있어요. 따라서 보조해는 다음과 같이 주어집니다.
\begin{align}
\tag{2-7}
u_h = A \cos (\theta + \theta_0)
\end{align}
한편 특성해 \(u_p\)를 구해야 하는데요. (2-5)식의 우변을 해라고 가정하면 \(u=k/ml^2\)로 쓸 수 있고, 이를 (2-5)식에 다시 대입해봐요. 그러면 다음을 얻을 수 있어요.
\begin{align}
\tag{2-8}
\color{red}{{{d^2}\over{d\theta^2}}\Big({{k}\over{ml^2}}\Big)} + {{k}\over{ml^2}} = {{k}\over{ml^2}}
\end{align}
이때, 윗 식의 빨강색 수식 부분이 0이 된다면 좌변과 우변이 같아져 \(u=k/ml^2\)가 해임을 알 수 있어요. 바로 이 해가 특성해 \(u_p\)인 것이죠.
일단 빨강색 수식에서 \(k\)와 \(m\)은 상수이므로 신경쓸 필요가 없고 단지 단위질량당 각운동량인 \(l\)이 \(\theta\)에 의존하느냐가 중요한 문제가 됩니다.
일단 행성의 각운동량은 보존됩니다. 따라서 단위질량당 각운동량도 보존이 되어 \(dl/dt=0\)의 관계가 성립해요. 그리고 이 관계를 연쇄규칙을 사용하여 변형하면 다음과 같이 쓸 수 있어요.
\begin{align}
\tag{2-9}
{{dl}\over{d \theta}}{{d \theta}\over{dt}} =0
\end{align}
이때 행성의 각속도 \(d\theta/dt\)는 0이 아니므로 윗 식이 성립하기 위해서는 \(dl/d\theta=0\)이 성립되어야 함을 알 수 있어요. 따라서 이 관계를 이용해 (2-8)식의 빨강생 부분만을 다시 정리하면 아래와 같아요.
\begin{align}
\tag{2-10}
\color{red}{{{d^2}\over{d\theta^2}} \Big( {{k}\over{ml^2}}\Big)} &= {{k}\over{m}} {{d}\over{d \theta}}(l^{-2})\\[8pt]
&={{k}\over{m}}(-2l^{-3}){{dl}\over{d \theta}}\\[8pt]
&=0
\end{align}
결국 (2-8)식의 빨강색 수식이 0이므로, \(k/ml^2\)가 특성해가 됩니다. 그래서 다음과 같이 쓸 수 있어요.
\begin{align}
\tag{2-11}
u_p = {k \over {ml^2}}
\end{align}
결국 (2-6)식에 보조해 (2-7)식과 특성해 (2-11)식을 대입하여 일반해를 구하면 아래와 같아요. 이때 초기 위상 \(\theta_0\)는 편의상 0으로 처리하도록 하겠습니다.
\begin{align}
\tag{2-12}
u = A \cos \theta + {{k}\over{ml^2}}
\end{align}
2-3. 이심율과 궤도식
위 (2-12)식에 (1-2)식의 관계를 적용해 \(r\)의 함수로 되돌리면 다음과 같아요.
\begin{align}
\tag{2-13}
{1 \over r} = A \cos \theta + {{k}\over{ml^2}}
\end{align}
또 윗 식을 \(r\)에 대해 정리하면 다음과 같죠.
\begin{align}
\tag{2-14}
r = {1 \over{A \cos \theta + k/ml^2}} = {{ml^2}\over{Aml^2 \cos \theta}+k}
\end{align}
그리고 윗 식 우변의 분모와 분자를 \(k\)로 나누면 다음의 식을 얻을 수 있어요.
\begin{align}
\tag{2-15}
r = {{ml^2 /k}\over{1+(A ml^2 /k ) \cos \theta}}
\end{align}
이때 윗 식의 분모에 있는 다음의 항을 \(\epsilon\)으로 치환하고 이심율이라고 불러요.
\begin{align}
\tag{2-16}
\epsilon = {{Aml^2}\over{k}}
\end{align}
이심율을 통해 (2-15)식을 다시 표현하면 아래와 같습니다. 이때 \(ml^2/k\)은 \(\alpha\)로 치환할게요.
\begin{align}
\tag{2-17}
r = {{\alpha}\over{1+\epsilon \cos \theta}}
\end{align}
그런데 이때 이심율이 \(\epsilon =0\)이면 원, \(0<\epsilon<1\)이면 타원, \(\epsilon=1\)이면 포물선, \(\epsilon>1\)이면 쌍곡선 궤도가 만들어지게 됩니다.
실제 태양계의 행성들은 타원궤도로 공전하고 있어요. 행성의 이심율을 구해보면 \(0<\epsilon<1\)의 조건을 만족하죠.
이를 케플러 제1법칙, 타원궤도의 법칙이라고 부릅니다.
3. 지구의 공전 타원 궤도
태양을 중심으로 공전하는 지구의 이심율은 \(\epsilon=0.0167\)입니다. 이 값을 반영해 실제 궤도 모양을 그려보면 다음과 같아요. 단 여기서 \(\alpha\)는 10으로 대입했습니다.
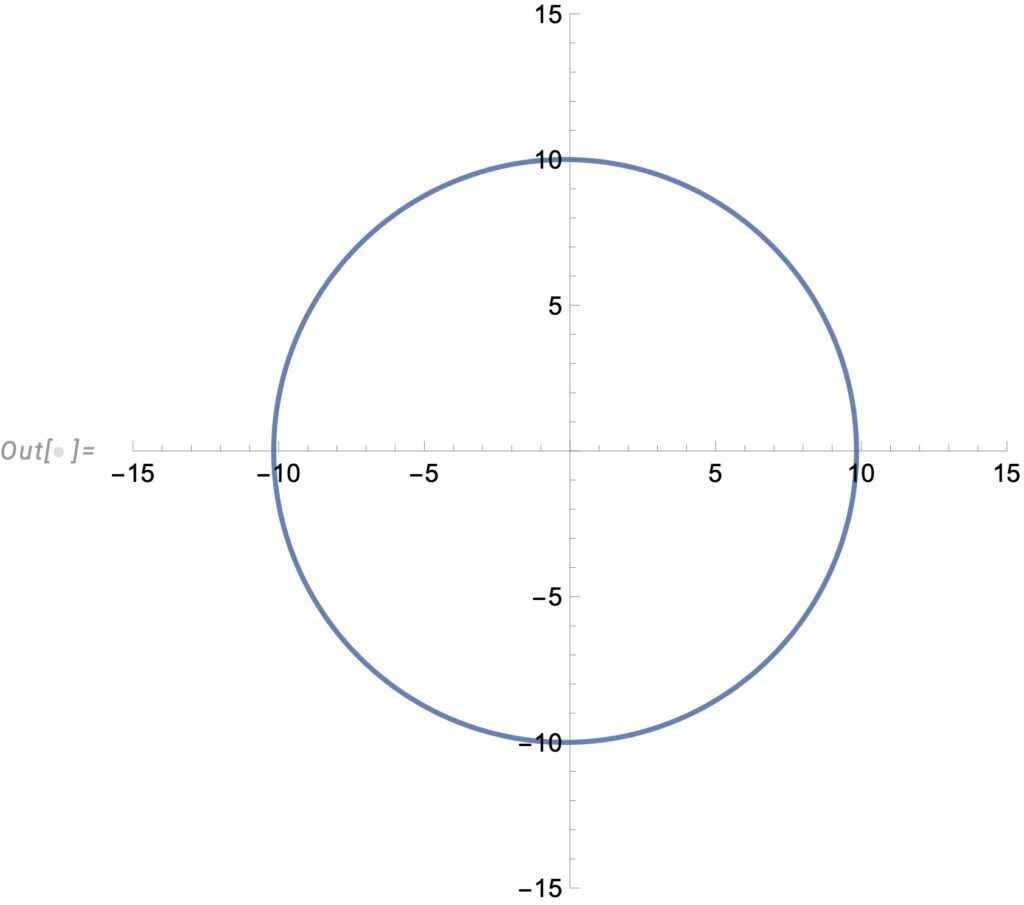
그림과 같이 얼핏 보면 지구의 공전궤도가 원으로 보이지만 실제로는 약간 찌그러진 타원이에요.