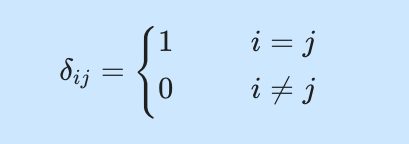Last Updated on 2025-08-26 by BallPen
함수값이 1 또는 0이 되는 크로네커 델타를 알아 봐요.
크로네커 델타(Kronecker delta)의 성질과 그 적용 예시를 이번 글에서 알아 봐요.
Contents
1. 크로네커 델타
크로네커 델타는 레오폴드 크로네커(Leopold Kronecker, 독일, 1823-1891)의 이름에서 유래되었어요.
크로네커 델타 \delta_{ij}의 성질은 아래와 같이 정수로 정의되는 두 변수 i와 j가 같은 값을 가지면 1, 다른 값을 가지면 0이 되는 함수를 말합니다.
\tag{1}
\delta _ {ij} = \left\{
\begin{align*}
1 ~~~~~~~~~~i=j\\
0~~~~~~~~~~i \ne j
\end{align*}
\right.예를 들어 \delta_{11}=1, \delta_{21}=0, \delta_{32}=0, \delta_{33}=1이 되는 방식이죠.
2. 크로네커 델타 성질
크로네커 델타의 성질이 사용되는 대표적인 사례는 다음과 같아요.
\tag{2}
\sum_{n=1}^{\infty} G_n \delta_{mn} = G_m즉, G_n \delta_{mn}을 모두 합하면 m번째 G_m를 구할 수 있어요.
예를 들어 G_n=2n이고 크로네커 델타가 \delta_{3n}으로 주어졌다면 다음과 같이 G_3의 값이 얻어지는 것과 같죠.
\begin{align}
\tag{3}
\sum_{n=1}^{5} G_{n}\delta_{3n} &= G_1 \delta_{31} + G_2 \delta_{32}+G_3 \delta_{33}+G_4 \delta_{34}+G_5 \delta_{35}\\[8pt]
&=G_3
\end{align}
결국 위 식의 결과는 G_3 = 2 \times 3 = 6이 됩니다.
물론 (2)식에서 G_m을 G_n으로 표기해도 상관없어요. 왜냐면 n=m인 경우에만 (2)식이 성립하니까요.
3. 예시
예를 들어 아래의 식은 삼각함수의 직교성에 따라 다음 관계가 성립합니다.
\tag{4}
\int_0^a \Big(\sin {{n \pi}\over{a}} y \sin {{m\pi}\over{a}}y\Big) ~dy =
\left\{
\begin{align*}
&0~~~~~~~~~~ n \ne m\\[8pt]
&{{a} \over {2}}~~~~~~~~~~ n=m\\
\end{align*}
\right.
윗 식에서 n과 m은 정수인데요. 그 정수가 서로 다른 값을 가지면 적분 결과가 0, 같은 값을 가지면 적분결과가 {a \over 2}가 됩니다.
(4)식을 크로넥커 델타 \delta_{nm} 기호를 사용하면 다음과 같이 간단히 표기할 수 있어요.
\tag{5}
\int_0^a \Big(\sin {{n \pi}\over{a}} y \sin {{m\pi}\over{a}}y\Big) ~dy = {a \over 2} \delta_{nm}마지막으로 (5)식을 \delta_{nm}에 대해 정리하면 다음과 같습니다.
\tag{6}
\delta_{nm} = {2 \over a} \int_0^a \Big(\sin {{n \pi}\over{a}} y \sin {{m\pi}\over{a}}y\Big) ~dy