회전운동 – 각위치, 각변위, 각속도, 각가속도의 정의와 개념

Last Updated on 2023-12-09 by BallPen

병진운동과 비교하여 회전운동에서의 각위치, 각변위, 각속도, 각가속도의 정의, 공식, 계산 방법을 알아보겠습니다.

회전운동 상태를 명확히 기술하기 위해서는 이와 관련된 몇 가지 주요 개념을 이해해야 합니다. 바로 각위치, 각변위, 각속도, 각가속도가 그것들인데요.

이러한 개념들은 병진운동에서의 위치, 변위, 속도, 가속도의 개념과 비교하여 이해하면 아주 재미있어요.

여기서 회전운동이란 고정된 회전축을 중심으로 물체가 회전하는 것을 말하며, 병진운동이란 물체의 모든 부분이 옆으로 이동해 나가는 현상을 말합니다.

예를 들어 아래 [그림 1]과 같이 CD가 플레이어 안으로 들어가면 CD가 회전하게 되잖아요. 이것이 회전운동의 한 예에요.

병진운동은 물체가 옆으로 이동하는 현상을 말하는데요. 아래 [그림 2]와 같이 기차가 철길을 따라 이동하고 있습니다. 이것이 병진운동입니다.

회전운동과 병진운동의 가장 큰 차이점은 회전운동은 회전체의 질량 중심이 회전축에 고정되어 이동하지 않지만 병진운동은 질량 중심 자체가 이동한다는 거에요.

만약 회전하면서 이동하는 물체가 있다면 그것은 회전운동과 병진운동의 복합운동에 해당합니다.

아래는 이번 글의 목차입니다.

1. 회전운동 상태에서의 각위치

회전운동에서의 각위치는 병진운동에서의 위치 개념에 대응할 수 있어요.

1-1. 위치 (병진운동)

어떤 기준점으로부터 동쪽으로 10 m 떨어진 곳에 물체가 있다고 생각해 보세요. 병진운동에서의 위치란 바로 그 거리와 방향을 뜻하는 것입니다. 따라서 위치 벡터 \vec d의 표기는 바로 아래 (1)식과 같이 표현하면 됩니다.

\tag{1}
\begin{align}
\vec d=10~ \mathrm{m} ~(동쪽 ~방향)
\end{align}

1-2. 각위치

그렇다면 회전운동에서의 각위치란 무엇일까요? 고정된 위치에서 회전만 할 뿐 이동하지 않으므로 병진운동에서의 위치 개념을 그대로 적용하면 항상 0 m가 되겠죠. 따라서 회전운동에서는 위치에 대응하는 다른 정의가 필요합니다.

바로 각도를 이용하는 것이죠.

예를 들어 아래 [그림 3]을 보시면 빨간색으로 표기된 기준축이 있습니다. 이때 원판이 회전하여 노란색 띠가 기준축으로부터 얼마의 각도 \theta만큼 회전되었느냐가 바로 각위치 개념입니다.

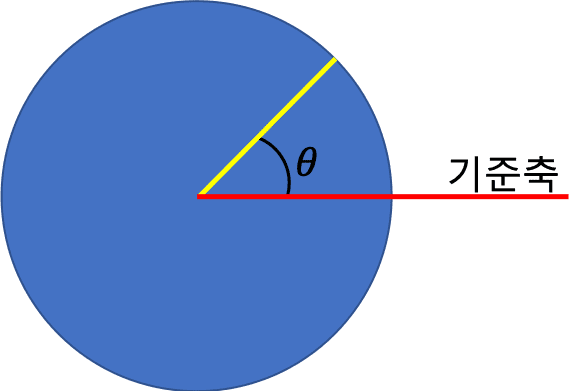
따라서 각위치를 표기하기 위해서 각도를 이용하면 되는데요. 평면각은 60분법 또는 호도법을 이용해 표기할 수 있습니다.

예를 들어 [그림 3]에서 표기된 \theta가 60분법으로 45^{\circ}일 때 각위치는 어떻게 표현하면 될까요?

바로 아래의 식(2)와 같이 표기합니다.

\begin{align}
\tag{2} &\theta = 45^{\circ} \\
\end{align}

또는 호도법을 이용해 (3)식과 같이 표기해도 됩니다. 60분법을 호도법으로 바꾸는 요령은 여기를 참고하세요.

\tag{3} \theta = 0.79 ~\mathrm{rad}

지금까지 위치와 각위치를 알아보았습니다. 병진운동에서의 위치는 거리의 단위를 갖고, 회전운동에서의 각위치는 각도의 단위를 갖는다는 것을 꼭 기억하세요.

2. 회전운동 상태에서의 각변위

이번에는 각변위입니다.

회전운동에서의 각변위는 병진운동에서의 변위 개념에 대응할 수 있어요.

2-1. 변위 (병진운동)

기준점으로부터 오른쪽 방향으로 처음위치 10 m에 있던 어떤 물체가 기준점으로부터 같은 방향으로 나중위치가 15 m로 바뀌었다고 생각해보세요. 병진운동에서의 변위란 나중위치 벡터 \vec d_2에서 처음위치 \vec d_1를 뺀 값을 말합니다.

따라서 변위 \Delta \vec d는 아래 (4)식과 같이 계산하면 되요.

\tag{4}
\begin{align}
\Delta\vec d &= \vec d_2 - \vec d_1\\
&=15~ \mathrm{m} - 10 ~\mathrm{m}\\
&=5~\mathrm{m}~~ (오른쪽 방향)
\end{align}

이때 (4)식에서 \Delta d위에 화살표를 붙이고 “오른쪽 방향”이라고 표기도 했는데요. 그 이유는 변위가 크기와 방향을 갖는 벡터량이기 때문입니다. (4)식에 따르면 변위의 크기는 5 m가 되고 방향은 오른쪽 방향이라는 뜻입니다.

2-2. 각변위

그렇다면 회전운동에서의 각변위란 무엇일까요? (4)식과 유사하게 생각하면 됩니다. 바로 나중 각위치에서 처음 각위치를 빼는 거에요.

아래 [그림 4]를 보세요. 노란색 띠가 처음 각위치 \theta_1에 있었어요. 그런데 이 원판이 반시계방향으로 회전하여 나중 각위치 \theta_2가 되었다고 생각해 보세요.

이때 각변위는 나중 각위치 \theta_2에서 처음 각위치 \theta_1을 빼면 구할 수 있어요.

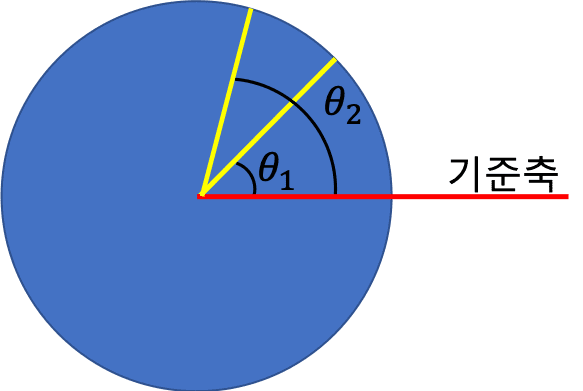
각변위 \Delta \theta를 공식으로 표현하면 아래 (5)식과 같습니다.

\tag{5}
\begin{align}
\Delta \theta = \theta_2 - \theta_1
\end{align}

그렇다면 [그림 4]에서 \theta_1이 0.79 rad이고 \theta_2가 1.31 rad이라면 각변위는 얼마일까요?

아래 (6)식처럼 계산하면 됩니다.

\tag{6}
\begin{align}
\Delta \theta &= \theta_2 - \theta_1 \\
&=1.31 ~\mathrm{rad} - 0.79 ~\mathrm{rad}\\
&=0.52 ~\mathrm{rad}
\end{align}

각변위는 0.52 rad입니다.

3. 회전운동 상태에서의 각속도

이번에는 각속도입니다.

회전운동에서의 각속도는 병진운동에서의 속도 개념에 대응됩니다.

3-1. 속도 (병진운동)

병진운동에서 속도란 이동하는 물체의 빠르기와 방향을 표현하는 수단입니다. 즉 속도의 크기가 클수록 물체는 빠르게 움직이는 것으로 볼 수 있습니다.

속도는 위에서 설명한 변위를 사용하여 정의합니다. 즉 주어진 변위가 얼마의 시간동안 일어나느냐인 것이죠.

공식으로 표현하면 아래의 (7)식과 같습니다.

\tag{7}
\begin{align}
\vec v = {{\Delta \vec d}\over{\Delta t}} ~(변위와 ~동일한 ~방향)
\end{align}

단위는 m/s이고 방향은 변위의 방향과 동일합니다.

예를 들어, 나중 위치벡터에서 처음 위치벡터를 뺀 변위벡터 \Delta \vec d가 북쪽으로 34.0 m인데, 이 변위가 31.0초 동안 일어났다면 속도는 얼마일까요?

아래 (8)식처럼 계산하면 됩니다.

\tag{8}
\begin{align}
\vec v &= {{\Delta \vec d}\over{\Delta t}}\\
&={{34.0 ~\mathrm{m}}\over{31.0~\mathrm{s}}}\\
&=1.10 ~\mathrm{m/s}~ (북쪽 방향)
\end{align}

속도의 크기는 1.10 m/s이고 방향은 변위와 동일하게 북쪽을 향합니다.

3-2. 각속도

그렇다면 회전운동에서의 각속도란 무엇일까요? 회전하는 빠르기와 관련이 있습니다. 각속도의 크기가 상대적으로 클수록 빠르게 회전합니다.

각속도도 (7)식으로 주어진 병진운동에서의 속도 표현과 동일한 방식으로 이해하면 됩니다.

즉, (5)식에 주어진 각변위 \Delta \theta를 변위가 일어나는 시간 \Delta t로 나누어 회전 빠르기의 척도인 각속도 \vec \omega의 크기를 구합니다.

이를 공식으로 표현하면 아래 (9)식과 같습니다.

\tag{9}
\begin{align}
\vec \omega &= {{\Delta \theta}\over{\Delta t}} ~(방향은~오른손~법칙을 ~따름)
\end{align}

이때 \omega위에 화살표가 붙어있어요. 바로 각속도가 벡터이기 때문입니다.

그런데 각속도의 크기는 (9)식을 이용해서 구하면 되는데요. “방향은 오른손법칙을 따름”이라고 표기되어 있어요. 오른손법칙이란 아래 [그림 5]와 같이 물체의 회전방향에 맞추어 오른손 네 손가락을 감아쥔 후 엄지를 펼쳤을 때 향하는 방향을 말해요.

따라서 [그림 4]와 같이 원판이 반시계방향으로 회전하는 경우 각속도의 방향은 원판에서 수직하게 나오는 방향, 즉 화면으로부터 나오는 방향이 됩니다.

그런데 여기서 많은 사람들이 각속도의 방향이 무슨 의미를 갖느냐라고 생각할 수도 있어요. 일단은 물리적 약속이라고 생각하시면 편합니다.

그리고 어떤 사람은 회전하는 물체의 접선방향을 각속도 방향으로 잡는 것이 좋지 않나하고 생각하는 분도 계신데요. 접선 방향을 각속도 벡터로 정하면 경우에 따라 크기는 동일할수 있지만 방향이 모두 다르기 때문에 각속도 벡터 방향으로는 타당하지 않습니다.

참고로 혹시 벡터가 익숙치 않다면 여기를 클릭해서 벡터를 공부할 수 있어요.

예제를 하나 풀어보죠. [그림 4]처럼 반시계방향으로 어떤 원판이 회전하고 있습니다. 15.0 s 동안 나중 각위치에서 처음 각위치를 뺀 각변위가 0.520 rad이라면 각속도는 어떻게 될까요?

아래 (10)식과 같이 계산하면 됩니다.

\tag{10}
\begin{align}
\vec \omega &= {{\Delta \theta}\over{\Delta t}}\\
&={{0.520 ~\mathrm{rad}}\over{15.0~ \mathrm{s}}}\\
&=0.0347 ~\mathrm{rad/s}~(화면으로부터 ~나오는 ~방향)
\end{align}

한편 각속도와 각속력이 헷갈리는 경우가 있는데요. 위에서 말씀드렸듯이 각속도는 벡터이므로 크기와 방향을 갖는 물리량입니다. 그런데 그중에서 크기 만을 말할 때 우리는 각속력이라고 합니다.

(10)식의 결과에서 ‘0.0347 rad/s’라고 크기만 표현하면 각속력을 말한 것이고, ‘화면에서 나오는 방향으로 0.0347 rad/s’라고 하면 각속도를 표현한 것입니다.

속력이 속도의 크기인 것과 같은 이치입니다.

4. 회전운동 상태에서의 각가속도

다음에는 각가속도를 설명드립니다.

회전운동에서의 각가속도는 병진운동에서의 가속도 개념에 대응됩니다.

4-1. 가속도 (병진운동)

병진운동에서 가속도란 단위시간당 속도의 변화량을 표현하는 수단입니다. 그러므로 가속도의 크기가 클수록 속도의 변화가 많이 나타납니다.

이때 속도의 변화가 많이 나타난다는 표현을 빠르다는 말로 오해하면 안됩니다. 느린 속도에서 빠른 속도로 급격히 가속되거나 반대로 빠른 속도가 급격히 느려진다는 표현으로 이해하시면 됩니다.

또한 가속도가 0인 물체는 속도가 변하지 않는 등속도운동을 하게 됩니다. 또한 가속도가 항상 일정한 운동을 등가속도운동이라고 부릅니다.

가속도 \vec a를 식으로 표현하면 아래(11)식과 같습니다.

\tag{11}
\begin{align}
\vec a &= {{\Delta \vec v}\over{\Delta t}}\\
&= {{\vec v_2 - \vec v_1}\over{\Delta t}} (속도벡터의 ~변화~ 방향)
\end{align}

(11)식과 같이 나중속도 \vec v_2에서 처음속도 \vec v_1을 뺀 속도의 변화량 \Delta \vec v를 경과시간 \Delta t로 나누면 가속도 \vec a를 구할 수 있습니다.

예를 들어 처음속도 20.0 m/s로 남쪽으로 움직이던 자동차가 45.0 s동안 가속되어 55.0 m/s가 되었다면 가속도는 얼마일까요?

\tag{12}
\begin{align}
\vec a &= {{\vec v_2 - \vec v_1}\over{\Delta t}}\\
&= {{55.0 ~\mathrm{m/s}-20.0~\mathrm{m/s}}\over{45.0 ~\mathrm{s}}}\\
&=0.778~\mathrm{m/s^2}~(남쪽~방향)
\end{align}

가속도는 남쪽 방향으로 0.778 m/s² 입니다.

4-2. 각가속도

회전운동에서의 각가속도란 무엇일까요? 가속도와 유사하게 단위시간당 각속도의 변화량을 각가속도라 합니다.

각가속도의 크기가 크면 회전하는 물체가 빠르게 빨라지고, 각가속도의 크기가 작으면 천천히 빨라지는 것으로 보시면 됩니다.

예를 들어 화물칸이 비어있는 트럭이 정지상태에 있습니다. 가속페달을 밟으면 바퀴가 정지상태에서 빠르게 회전하는 각속도 상태로 바뀌는 것을 볼 수 있습니다. 이러한 경우는 각가속도의 크기가 큰 경우입니다. 바퀴가 각속도 0인 상태에서 각속도가 큰 상태로 변하는데 걸리는 시간이 매우 짧기 때문이죠.

반대로 화물을 가득실은 정지한 트럭의 가속페달을 밝을때, 트럭의 바퀴를 보면 정지상태에서 회전 각속도가 큰 상태로 서서히 변하는 것을 볼 수 있습니다. 이러한 경우는 각가속도의 크기가 작은 경우에 해당합니다. 바퀴가 각속도 0인 상태에서 각속도가 큰 상태로 변하는데 걸리는 시간이 매우 길기 때문이죠.

각가속도가 0인 물체는 각속도가 변하지 않는 등각속도운동을 하게 됩니다. 또한 각가속도가 항상 일정한 운동을 등각가속도운동이라고 부릅니다.

각가속도 \vec \alpha를 공식으로 표현하면 아래 (13)식과 같습니다. 단위는 rad/s²입니다.

\tag{13}
\begin{align}
\vec \alpha &= {{\Delta \vec \omega}\over{\Delta t}}\\
&={{\vec \omega_2 - \vec \omega_1}\over{\Delta t}}(각속도 벡터의 ~변화~ 방향)
\end{align}

(13)식과 같이 나중 각속도 \vec \omega_2에서 처음 각속도 \vec \omega_1을 뺀 각속도의 변화량 \Delta \vec \omega를 경과시간 \Delta t로 나누어 각가속도 \vec \alpha를 구합니다.

예제 하나를 풀어보겠습니다. [그림 4]와 같이 반시계방향으로 처음 각속도 8.00 rad/s로 회전하던 원판이 12.0 s 동안 점점 빨라져 12.0 rad/s로 되었다면 각가속도는 얼마일까요?

\tag{14}
\begin{align}
\vec \alpha &={{\vec \omega_2 - \vec \omega_1}\over{\Delta t}}\\
&={{12.0~\mathrm{rad/s}-{8.00~\mathrm{rad/s}}}\over{12.0~\mathrm{s}}}\\
&= 0.333~\mathrm{rad/s^2} ~(화면으로부터~ 나오는~ 방향)
\end{align}

각가속도는 화면으로부터 나오는 방향으로 0.333 rad/s² 입니다.

5. 개념 정리

• 회전운동에서의 각위치는 병진운동에서의 위치에 대응한다. 각위치의 단위는 보통 rad으로 표현된다.
• 회전운동에서의 각변위는 병진운동에서의 변위에 대응한다. 각변위는 각위치의 변화량으로 정의되며 단위는 rad이다.
• 회전운동에서의 각속도는 병진운동에서의 속도에 대응한다. 각속도는 회전빠르기의 척도로서 단위시간당 각변위로 정의되며 단위는 rad/s이다.
• 회전운동에서의 각가속도는 병진운동에서의 가속도에 대응한다. 각가속도는 각속도 변화의 척도로서 단위시간당 각속도의 변화량으로 정의되며 단위는 rad/s²이다.

Related posts.

각운동 – 각속도와 접선속도, 각가속도와 접선가속도의 관계 자동차 배기량(displacement)의 정의와 어떻게 계산하는지를 알아볼까요? 단위 표기 오류가 있는 도쿄 올림픽 중계방송이 불편한 이유 에너지 절약 – 정말 TV 시청 시간 줄인다고 에너지가 절약 되나요? 측정 – 정확도와 정밀도의 개념, 계산, 표기 방법 등가소음도 연습 문제 원심분리기 원리와 RPM, RCF, G 값의 차이 높이에 따른 위치에너지 변화