Last Updated on 2024-03-04 by BallPen
자연과학이나 공학에서는 측정값의 불확정도를 감안하여 숫자를 계산합니다. 이때 사용하는 것이 유효 숫자입니다.
유효 숫자 (significant figure)란 측정을 통해 기록되는 숫자 중 의미가 있다고 판단되는 숫자를 말합니다.
과학이나 공학자들은 어떤 이론을 검증하거나 실험을 수행하기 위해 수많은 측정을 하는데요. 이러한 측정을 통해 우리 인류에게 도움이 되는 새로운 이론이나 기술이 탄생하게 됩니다.
현대 과학 기술에서 측정이라 함은 센서를 이용한 변환단계(sensor transducer), 신호 조정 단계(signal conditioning), 기록 단계(readout, recording)가 종합된 개념으로 볼 수 있습니다.
이때 기록단계에서 숫자로 된 측정 데이터를 연산해야 하는 경우가 많은데요. 이 과정에서 숫자의 자릿수를 어디까지 표기해야 하는지에 대한 기준이 필요합니다.
이때 필요한 것이 유효 숫자 개념입니다.
1. 측정 사례
여러분이 어느 기준점으로부터 종이에 표기된 어느 선까지의 길이를 30 cm 자로 측정한다고 생각해보세요. 아래에 두개의 이미지가 있습니다.
1-1. 첫번째 측정 사례
빨간색 화살표가 있는 선에 걸친 눈금을 읽어보세요.

15.3 cm와 15.4 cm의 중간에 선이 놓여있습니다. 많은 사람들은 15.35 cm라고 측정하고 기록할거에요.
1-2. 두번째 측정 사례
이번에는 아래 이미지에서 파랑색 화살표가 있는 선에 걸친 눈금을 읽어보세요.

16.4 cm의 눈금에 선이 완전히 겹쳐진 것 같아요. 그러면 눈금을 16.4 cm라고 읽고 기록하면 될까요?
2. 유효 숫자 개념
위의 첫번째 사진에서는 눈금을 15.35 cm라고 기록하고 두번째 사진에서는 16.4 cm라고 기록했습니다. 이게 올바른 측정값 기록일까요?
측정의 불확정도 또는 정밀도 관점에서 한번 생각해 봅시다. 이때 여기서 말하는 정밀도는 측정 분해능(measurement resolution)의 관점에서의 표현이고 우연오차에 의해 발생되는 정밀도(precision)와는 다른 개념입니다.
첫번째 사진에서 측정하여 기록한 15.35 cm는 15.3 cm와 15.4 cm의 중간에 선이 놓여 있기 때문에 신경써서 정밀하게 측정한 값입니다.
또한 두번째 사진에서 측정하여 기록한 16.4 cm도 선이 눈금과 일치되어 기록한 값입니다. 그런데 만일 16.4 cm보다 조금 길었다면 우리는 16.41 cm로도 측정할 수도 있었고 16.4 cm보다 조금 부족했다면 16.39 cm로도 측정할 수 있었을거에요.
따라서 정밀도 관점에서 두번째 기록인 16.4 cm는 우리가 0.01 cm까지 정밀하게 읽을 수 있는 능력이 있다는 정보를 누락한 기록에 해당합니다.
왜냐면 첫번째 사진에서는 0.01 cm까지 정밀하게 기록한 반면에 두번째 사진에서는 0.1 cm까지만 기록했기 때문입니다. 그러므로 우리가 읽을 수 있었던 정밀도를 정확하게 표기하기 위해서는 두번째 측정의 기록을 16.4 cm가 아닌 16.40 cm라고 기록해야 하는 것이죠.
물론 수학에서는 16.4와 16.40은 같은 크기를 갖는 숫자로 처리합니다만, 과학적 기록에서는 16.40 cm의 기록이 16.4 cm보다 더욱 정밀한 측정이 이루어진 것으로 간주합니다.
노력해서 정밀하게 읽은 값이면 그 정밀한 정도를 숫자에 표기를 해주어야 합니다.
그게 바로 유효한 숫자, 즉 유효 숫자를 사용하는 이유입니다.
그렇다면 이런 경우는 어떨까요? 여러분들이 정밀한 저울을 가지고 있어요. 그 저울로 물체의 질량을 측정했더니 28 g이 나왔습니다. 그러면 28 g이라고 기록하시면 되겠죠.
그런데 동일한 저울로 다른 물체를 측정했더니 100 g이 나왔습니다. 그러면 0.1 kg 이라고 기록하면 될까요? 아니요 0.100 kg 또는 100. g이라고 기록해야 합니다. 그래야 사람들이 1 g단위로 측정할 수 있는 저울을 사용했음을 알게 됩니다.
만일 0.1 kg이라고 표기하면 좋은 저울로 정밀하게 측정했음에도 정밀도가 안좋은 저울로 대충 측정한 값으로 오해합니다. 그러니까 0.1 kg 밑으로는 정밀하게 측정할 수 없는 저울로 측정한 값이라고 인식해버려요.
물론 16.40 cm로 측정하고 일부러 16.400 cm라고 유효 숫자 수를 늘려 정밀하게 측정한 것처럼 표기해서도 안되겠죠.
3. 유효 숫자 판정
그렇다면 누군가가 측정한 표기값에서, 무엇이 유효 숫자인지의 여부는 어떻게 판단할까요? 몇가지 규칙이 있으니 예시와 함께 설명드리겠습니다. 이 유효 숫자를 정확히 판정할 수 있어야 덧셈, 뺄셈 등의 정확한 연산이 가능합니다.
아울러 유효 숫자 여부를 명확히 표기하기 위해 보통 과학적 표기법이 주로 활용됩니다. 이에 대해서도 함께 참고하세요.
3-1. 모든 측정 값이 0이 아닌 숫자로 구성된 경우는 모두 유효 숫자
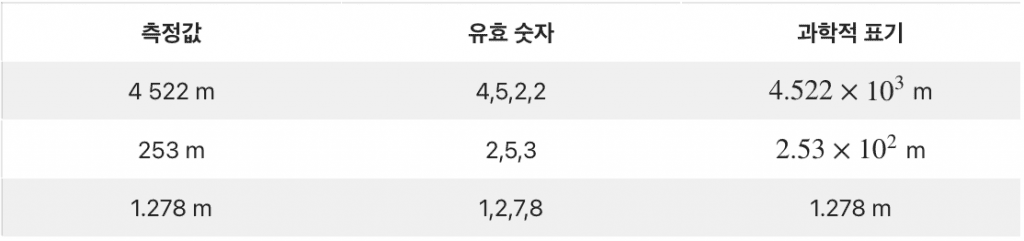
3-2. 0이 아닌 숫자로 둘러싸인 0은 유효 숫자
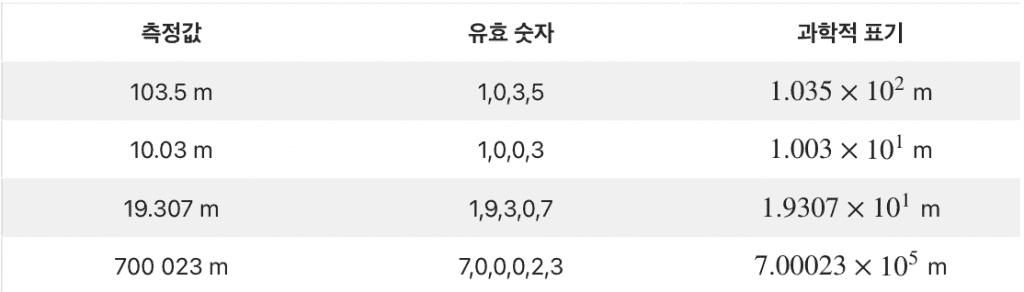
3-3. 단지 숫자의 크기를 표현하기 위해 붙은 0은 유효 숫자가 아님
단지 숫자의 크기를 표현하기 위해 붙혀진 0은 유효숫자가 아닙니다. 이러한 경우에는 과학적 표기법의 10의 지수 또는 단위 앞에 붙는 접두어에 따라 그 존재 여부가 달라질 수 있기 때문입니다.
이 경우에도 과학적 표기법을 활용하면 유효 숫자를 명확히 표기할 수 있습니다.
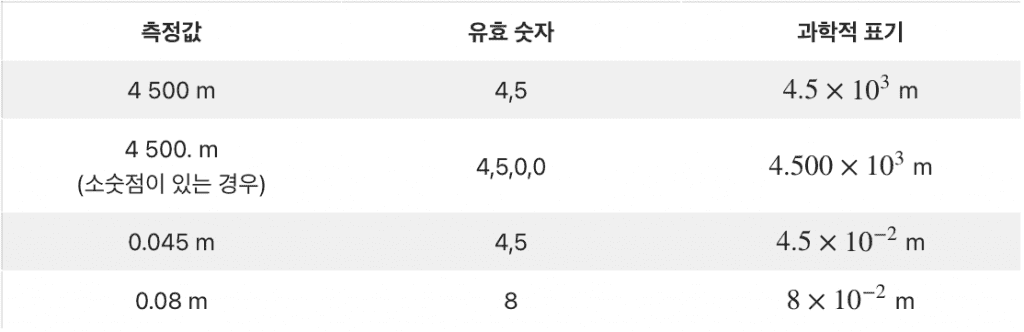
3-4. 소수점 아래의 끝에 있는 0은 유효 숫자

3-5. 과학 상수, 배수, 물건의 갯수를 셈한 것은 무한의 유효 숫자로 간주
아보가도로수 또는 중력가속도와 같은 과학적 상수나 물건의 갯수를 셈한 수치 등은 무한대의 유효 숫자를 갖는 것으로 간주합니다.
4. 유효 숫자 계산
4-1. 덧셈에서의 유효 숫자
두 숫자 끼리의 덧셈을 할 때 유효 숫자는 어떻게 처리해야 할까요? 결과 값의 표기는 연산되는 값 중에서 소수점 아래의 자리수가 가장 작은 것에 일치시켜야 합니다.
예를 들어 1.467은 소수점 아래의 자리수가 3개이고, 83.3은 소수점 아래 자리수가 1개입니다. 이 두 숫자를 더하면 84.767이 나오는데요. 결과값은 소수점 아래 자리수가 작은 1개에 맞추어서 기록하면 됩니다. 소수점 둘째자리에서 반올림하여 소수점 첫째자리까지만 표기하세요. 즉 결과값은 84.8이 됩니다.
간혹 정밀도(불확정도)가 크게 차이나는 경우에 대해서 고민하는 경우가 있습니다. 예를 들어 1236 m + 0.000001 m일 경우 결과값은 1236 m가 될 뿐입니다. 그렇다면 0.000001은 어디로 갔나하고 궁금할 수도 있을 텐데요.
사실 이러한 계산은 시도하지 않는게 좋습니다. 왜냐면 누군가가 m급 규모로 대충 측정한 큰 수치에 마이크로미터 급으로 아주 정밀하게 얻은 작은 수치를 더하는 것은 아무런 의미가 없기 때문입니다.
덧셈에 대한 계산 예시
| (숫자 A) + (숫자 B) | 결과 값 | 과학적 표기 |
|---|---|---|
| 1.467 m + 83.3 m (소수점 아래 자리수 3개와 1개) | 84.8 m (84.767의 소수점 둘째자리에서 반올림하여 소숫점 아래 1개로 표기) | 8.48 \times 10^1 m |
| 1.357 m + 83.3 m (소수점 아래 자리수 3개와 1개) | 84.6 (84.657의 소수점 둘째자리에서 반올림하여 소수점 아래 1개로 표기. 이때 둘째자리가 5인 경우에는 앞의 바로 앞의 숫자가 짝수인 경우 버림주1) | 8.46 \times 10^1 m |
| 1.457 m + 83.3 m (소수점 아래 자리수 3개와 1개) | 84.8 (84.757의 소수점 둘째자리에서 반올림하여 소수점 아래 1개로 표기. 이때 둘째자리가 5인 경우에는 앞의 바로 앞의 숫자가 홀수인 경우 올림 주1) | 8.48 \times 10^1 m |
| 11 m + 0.23 m (소수점 아래 자리수 0개와 2개) | 11 m (11.23의 소수점 첫째 자리에서 반올림하여 소수점 아래 0개로 표기. 0.23을 더했지만 불확정도를 감안할 때 그 효과가 미미하여 합한 효과가 무시되는 것임) | 1.1 \times 10^1 m |
| 11 m + 0.87 m (소수점 아래 자리수 0개와 2개) | 12 m (11.87의 소수점 첫째자리에서 반올림하여 소수점 아래 0개로 표기) | 1.2 \times 10^1 m |
| 9 m + 0.87 m (소수점 아래 자리수 0개와 2개) | 10. m (9.87의 소수점 첫째자리에서 반올림하여 소수점 아래 0개로 표기. 그리고 위 결과값에서 0이 유효숫자이므로 0 다음에 점을 찍어 주어야 함) | 1.0 \times 10^1 m |
| 12.23 m + 0.079 m (소수점 아래 자리수 2개와 3개) | 12.31 m (12.309의 소수점 세째자리에서 반올림하여 소수점 아래 2개로 표기) | 1.231 \times 10^{1} m |
4-2. 뺄셈에서의 유효 숫자
두 숫자 끼리의 뺄셈을 할 때에는 덧셈에서의 유효 숫자 처리 방식과 동일합니다. 즉 결과 값의 표기는 연산되는 값 중에서 소수점 아래 자리 수가 가장 작은 것에 일치시켜야 합니다.
뺄셈에 대한 계산 예시
예를 들어 123.344는 소수점 아래 자리수가 3개이고 5.6은 1개입니다. 이때 두 수의 뺄셈인 117.744를 소수점 둘째 자리에서 반올림하여 소수점 아래 자리수 1개까지만 기록합니다. 그래서 결과 값은 117.7이 됩니다.
| (숫자 A) – (숫자 B) | 결과 값 | 과학적 표기 |
|---|---|---|
| 123.344 m – 5.6 m (소수점 아래 자리수 3개와 1개) | 117.7 (117.744의 소수점 둘째자리에서 반올림하여 소수점 아래 1개로 표기) | 1.177 \times 10^{2} m |
| 126 m – 0.27 m (소수점 아래 자리수 0개와 2개) | 126 (125.73의 소수점 첫째자리에서 반올림하여 소수점 아래 0개로 표기) | 1.26 \times 10^{2} m |
| 0.45 m – 0.002 m (소수점 아래 자리수 2개와 3개) | 0.45 (0.448의 소수점 셋째자리에서 반올림하여 소수점 아래 2개로 표기) | 4.5 \times 10^{-1} m |
4-3. 곱셈에서의 유효 숫자
두 숫자 끼리의 곱셈을 할 때 유효 숫자는 어떻게 해야 할까요? 이 경우 결과 값의 표기는 연산되는 값 중에서 유효 숫자의 갯수가 가장 작은 것과 같게 일치시켜야 합니다.
예를 들어 4.56은 유효 숫자가 3개이고, 1.4는 2개입니다. 이 두 숫자를 곱하면 6.384가 나오는데요. 결과값은 유효 숫자의 갯수가 작은 2개에 맞추어서 기록하면 됩니다. 소수점 둘째자리에서 반올림하여 소수점 첫째자리까지 표기해 유효숫자의 갯수를 2개로 맞추면 됩니다. 결과값은 6.4입니다.
곱셈에 대한 계산 예시
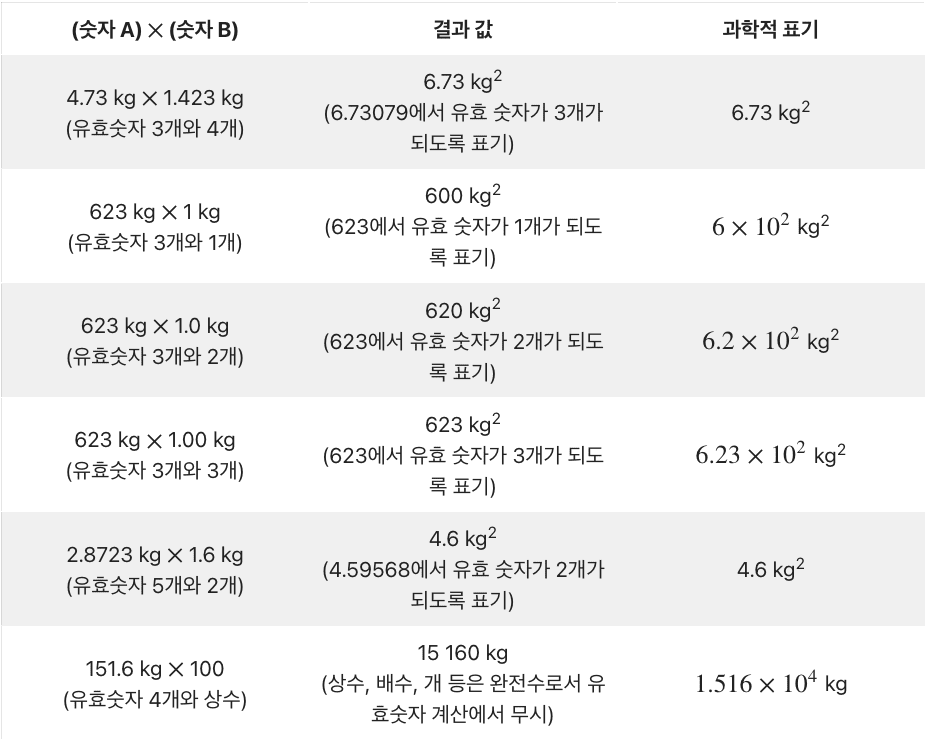
4-4. 나눗셈에서의 유효 숫자
두 숫자 사이의 나눗셈을 할 때에는 곱셈에서의 유효 숫자 처리 방식과 동일합니다. 즉 결과 값의 표기는 연산되는 값 중에서 유효 숫자의 갯수가 가장 작은 것에 일치시켜야 합니다.
나눗셈에 대한 계산 예시
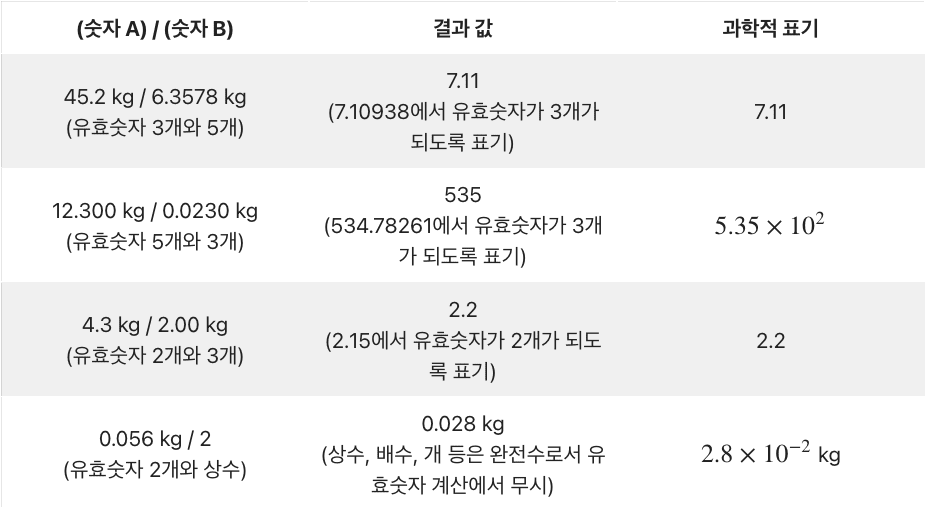
5. 유효 숫자 혼합 계산 예제
6. 유효 숫자 개념, 계산 및 표기 방법 요약
- 유효숫자란 측정을 통해 기록되는 숫자 중 의미가 있다고 판단되는 숫자를 말함
- 유효숫자 판정은 다음의 기준을 따름
– 모든 측정값이 0이 아닌 숫자로 구성된 경우는 모두 유효숫자
– 0이 아닌 숫자로 둘러싸인 0은 유효숫자
– 단지 숫자의 크기를 표현하기 위해 붙은 0은 유효숫자가 아님
– 소수점 아래의 끝에 있는 0은 유효숫자
– 상수 또는 물건의 갯수를 셈한 것은 무한의 유효숫자로 간주 - 덧셈과 뺄셈에서는 연산되는 값 중에서 소수점 아래 자리수가 가장 작은 것에 맞추어 결과값 표기
- 곱셈과 나눗셈에서는 연산되는 값 중에서 총 유효숫자의 갯수가 가장 작은 것에 맞추어 결과값 표기






0.45m-0.002m의 뺄셈이 0.4m가 된다고 하셨는데,
뺄셈은 소수점 이하의 개수를 따지는 것이므로 0.45m가 되는 것이 아닌지요.
단위 변환을 통해 생각해 보면,
0.45m = 45cm = 450mm
0.002m = 0.2cm = 2mm
뺄셈의 결과는 448mm이며, 유효숫자를 따르면 450mm가 되어야 하는 것 같습니다.
다른 예제로,
17m – 2m = 15m이지, 20m가 되지는 않을 것 같습니다.
0.45m-0.002m를 단위를 빼고 숫자로 생각하면,
0.45-0.002인데, 이 경우에도 0.45가 맞을 것 같습니다.
혹시 제가 생각하는 바가 잘못되었다면 메일 주시면 감사하겠습니다.
잘못된 오류를 지적해주셔서 감사합니다.
김준호님께서 말씀하신 내용이 맞습니다.
제가 실수를 했어요.
틀린 부분이 있을 때마다 수정해주시는 많은 분들이 계셔서 항상 감사할 뿐입니다.
틀린 부분 수정하였습니다.
감사합니다.
좋은 내용 감사합니다. 혹시 4장 유효숫자의 계산편의 내용이 담긴 관련 표준이나 책을 공유해 주신다면 더없이 많은 도움이 될 것 같습니다. 좋은 글 감사합니다!
방문해 주셔서 감사합니다.
말씀하신 유효숫자의 계산법을 구체적으로 설명하는 책은 의외로 찾아보기 힘듭니다. 다만 유효숫자 판정법과 유효숫자를 이용한 덧셈, 뺄셈 등의 계산 원칙이 실려있는 책은 많아요. 그런데 그 내용은 저의 블로그 내용과 거의 비슷합니다. 혹시라도 책을 원하신다면 서점에서 일반물리학 도서를 찾으시면 됩니다. 대부분 일반물리학의 서론 부분에서 유효숫자를 다루고 있습니다. 참고하시기 바랍니다.