입자의 궤도 방정식

Last Updated on 2025-08-22 by BallPen

중심력장 하에서 움직이는 입자의 궤도를 구하는 미분방정식을 알아 봐요.

입자의 궤도 방정식(differential equation of the orbit of a particle)이란 어떤 중심력(Central Force) 하에서 움직이는 입자가 무슨 궤도를 갖게 되는지를 구할 수 있는 미분방정식입니다.

이 방정식에 중심력을 대입하여 풀면 \(\theta\)의 함수로 원점으로부터 입자까지의 거리 \(r\)을 구할 수 있어요. 그래서 \(\theta\)의 범위에 따라 \(r\)의 값을 구한 후 연결하면 궤도의 모양을 알 수 있답니다.

결론부터 말씀드리면 아래의 식이 입자의 궤도 방정식이에요.

\begin{align}
\tag{D1}
{{d^2 u}\over{d \theta^2}} + u = – {1 \over{ml^2 u^2}} f(u^{-1})
\end{align}

여기서 \(u=1/r\)의 관계를 갖고, \(l\)은 단위질량당 각운동량을 뜻합니다. 그리고 \(f(u^{-1})\)은 중심력이에요.

윗 식을 풀면 \(\theta\)의 함수로 주어지는 \(u\)에 대한 식을 구할 수 있고, 그 \(u\)에 역수를 취하면 \(r(\theta)\)를 구하게 되는 것이죠.

이제부터 더 구체적으로 알아 봐요.

1. 중심력(Central Forces)

중심력장 하에서 입자의 궤도방정식을 구하고자 하므로 중심력에 대한 정의를 먼저 알아야 해요.

중심력이란 물체를 하나의 점으로 간주했을 때 이 점으로부터의 거리에만 의존하고 지름방향을 향하는 힘을 의미합니다.

대표적으로 질량 사이에 작용하는 만유인력과 전하 사이에 작용하는 전기력이 있어요.

이 글에서는 중심력장을 다음과 같이 표현할게요.

\begin{align}
\tag{1-1}
f(r) \hat {e_r}
\end{align}

위 식에서 단위벡터 \(\hat {e_r}\)은 중심으로부터 멀어지는 지름방향을 뜻합니다.

2. 입자의 궤도 방정식 유도

입자의 궤도방정식을 유도하기 위해서는 입자에 작용하는 힘에 대한 운동방정식부터 만들어야 해요.

2-1. 운동방정식

우리는 어떤 입자가 (1-1)식으로 주어지는 중심력을 받고 있을 때 그 입자가 어떤 궤도를 갖게 되느냐에 대해 궁금한 거에요.

이를 알기 위해서는 먼저 입자가 받는 중심력을 뉴턴의 운동 제2법칙에 적용하면 됩니다. 이를 운동방정식이라 하고 식으로 표현하면 다음과 같아요.

\begin{align}
\tag{2-1}
f(r) \hat {e_r} = m \ddot {\vec r}
\end{align}

윗 식에서 좌변은 중심력의 크기와 방향을 나타낸 거에요. 그리고 우변에서 \(m\)은 입자의 질량을, \( \ddot {\vec {r}} \)은 변위 \(\vec r\)를 시간으로 두번 미분한 가속도를 의미해요. 즉 \(\ddot {\vec r} = {{d^2 \vec r}/{dt^2}}\)을 의미합니다.

참고로 어떤 물리량 위에 점이 하나가 있다면 그것은 속도를 나타내요. 예를 들어 \(\dot {\vec r} = {{d{\vec r}}/{dt}}\)을 의미한다는 것을 기억하세요.

2-2. 궤도 방정식

(2-1)식의 운동방정식으로 \(r(\theta)\) 관계식을 얻기 위해서는 입자의 궤도를 편하게 다룰 수 있는 좌표계를 선택해야 해요.

예를 들어, 중심력장이 작용하는 태양계를 생각해보면 태양을 중심으로 행성은 평면위에서 회전하고 있음을 알고 있어요. 그러므로 평면 공간에서 입자의 운동을 편리하게 기술할 수 있는 극좌표계를 사용하면 좋을 것 같아요.

그래서 (2-1)식의 우변에 극좌표계에서의 가속도 공식을 적용하면 다음과 같아요.

\begin{align}
\tag{2-2}
f(r) \hat {e_r} = m (\ddot r – r {\dot \theta}^2) \hat {e_r} + (\color{blue}{2 \dot r \dot \theta + r \ddot \theta})\hat{e_{\theta}}
\end{align}

이때 좌변과 우변이 같기 위해서는 \(\hat{e_\theta}\)방향의 가속도(식에서 파랑색 부분)는 0이 되어야 해요. 중심력이 지름방향으로만 작용하기 때문에 가로방향 가속도는 0이 되어야 하는 것은 당연해요.

결국 (2-2)식의 운동방정식은 다음과 같이 표현할 수 있습니다.

\begin{align}
\tag{2-3}
f(r) \hat {e_r} = m (\ddot r – r {\dot \theta}^2) \hat {e_r}
\end{align}

[단위질량당 각운동량]

그런데 (2-2)식에서 파랑색 부분의 식을 잘 보면 다음 관계가 성립한다는 것을 알 수 있어요.

\begin{align}
\tag{2-4}
2 \dot r \dot \theta + r \ddot \theta &= {1 \over r} {{d}\over{dt}} \color{red}{(r^2 \dot \theta)}=0
\end{align}

이것은 윗 식에서 빨강색 부분인 \(r^2 \dot \theta\)이 시간에 의존하지 않는 상수일 때 가능해요.

그런데 이것이 무슨 물리적 의미가 있길래 상수가 되는지 궁금할 텐데요. 결론부터 말씀드리면 \(r^2 \dot \theta\)은 단위질량당 각운동량을 뜻해요. 중심력장 하에서 입자의 각운동량은 보존됩니다. 그래서 단위질량당 각운동량도 상수가 되는 것 뿐이에요.

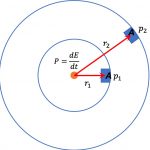
즉, 보존되는 점입자의 각운동량 크기 \(L\)를 아래와 같이 정리해봐요. 이때 \(p\)는 점입자의 선운동량이고, 접선속도와 각속도 사이의 관계인 \(v=r\omega\)의 관계를 적용했어요.

\begin{align}
\tag{2-5}
L = rp = mvr &= mr^2 \omega \\[8pt]
&= mr^2 \dot \theta
\end{align}

그리고 윗식의 마지막 줄을 단위질량당 각운동량으로 표현하면 아래와 같이 (2-4)식의 빨강색 수식이 도출됩니다. 상수이므로 편의상 \(l\)로 치환해 놓도록 할게요.

\begin{align}
\tag{2-6}
{{L}\over{m}} &= r^2 \dot \theta =l
\end{align}

[u=1/r의 도입]

(2-3)식의 운동방정식을 변형시켜 궤도 방정식을 도출하기 위해 \(r\)의 역수인 \(u\)를 도입해 봐요.

\begin{align}
\tag{2-7}
r = {1 \over u} = u^{-1}
\end{align}

한편 (2-6)식에 따르면 다음 관계가 성립합을 알 수 있어요.

\begin{align}
\tag{2-8}
\dot \theta = {{l}\over{r^2}} = u^2 l
\end{align}

그리고 (2-3)식에 대입할 수 있도록 속도 \(\dot r\)과 가속도 \(\ddot r\)의 크기도 구해보도록 해요. 먼저 (2-7)식을 시간으로 미분해 속도를 구하면 다음과 같습니다. 전개 과정중에 (2-8)식이 활용되었어요.

\begin{align}
\tag{2-9}
\require{cancel}
\dot r &= (-1)u^{-2} {{du}\over{dt}}\\[8pt]
&=- {1 \over u^2} {{du}\over{d \theta}} {{d \theta}\over{dt}}\\[8pt]
&=- {1 \over {u^2}} \dot \theta {{du}\over{d \theta}}\\[8pt]
&=-{1 \over {\cancel {u^2}}} {\cancel{u^2}} l {{d u}\over{d \theta}}\\
&=-l {{du}\over{d \theta}}
\end{align}

다음에는 위 (2-9)식을 시간으로 한번 더 미분해 가속도를 구하면 다음과 같아요.

\begin{align}
\tag{2-10}
\ddot r &= – l {{d}\over{dt}}\Big({{du}\over{d \theta}}\Big) \\[8pt]
&= -l {{d \theta}\over{dt}} {{d}\over{d \theta}} {{du}\over{d \theta}}\\[8pt]
&=-l\dot \theta {{d^2 u}\over{d\theta^2}}\\[8pt]
&=-l(u^2 l) {{d^2 u}\over{d\theta^2}}\\[8pt]
&=-l^2 u^2 {{d^2 u}\over{d \theta^2}}
\end{align}

2-3. 궤도방정식의 완성

그럼 이제 (2-3)식의 좌변와 우변을 서로 바꾼 후 (2-10)식, (2-7)식, (2-8)식을 대입하여 정리해봐요.

\begin{align}
\tag{2-11}
m(\ddot r – r {\dot \theta}^2) = f(r)
\end{align}

\begin{align}
\tag{2-12}
m \Big(-l^2 u^2 {{d^2 u}\over{d \theta^2}} – {1 \over u} {(u^2 l)}^2 \Big) = f(r)
\end{align}

\begin{align}
\tag{2-13}
-m l^2 u^2 \Big({{d^2 u}\over{d \theta^2}} + u \Big) = f(u^{-1})
\end{align}

최종적으로 위 (2-13)식을 정리하면 다음 미분방정식을 얻습니다. 이 식을 중심력장 하에서 움직이는 입자의 궤도 방정식이라고 불러요.

\begin{align}
\tag{2-14}
{{d^2 u}\over{d \theta^2}} + u = – {1 \over {ml^2 u^2}} f(u^{-1})
\end{align}

3. 예제

입자의 궤도 방정식인 (2-14)식에 중심력을 대입해 풀면 입자의 궤도 \(r (\theta)\)를 구할 수 있어요. 이 예제는 그와는 반대로 입자의 궤도를 궤도방정식에 대입해 중심력을 구해보는 문제에요.

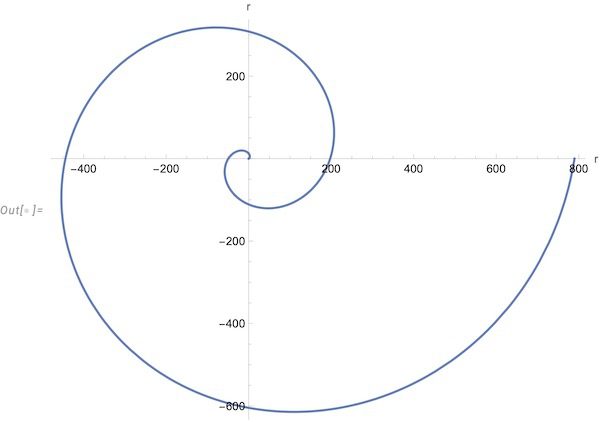
(예제) 중심력장에서 어떤 입자가 \(r=c\theta^2\)으로 주어지는 [그림 1]의 나선형 궤도를 따라 움직이고 있다. 이때 \(c\)는 상수이다. 이 궤도가 나타나기 위한 중심력을 구하여라.

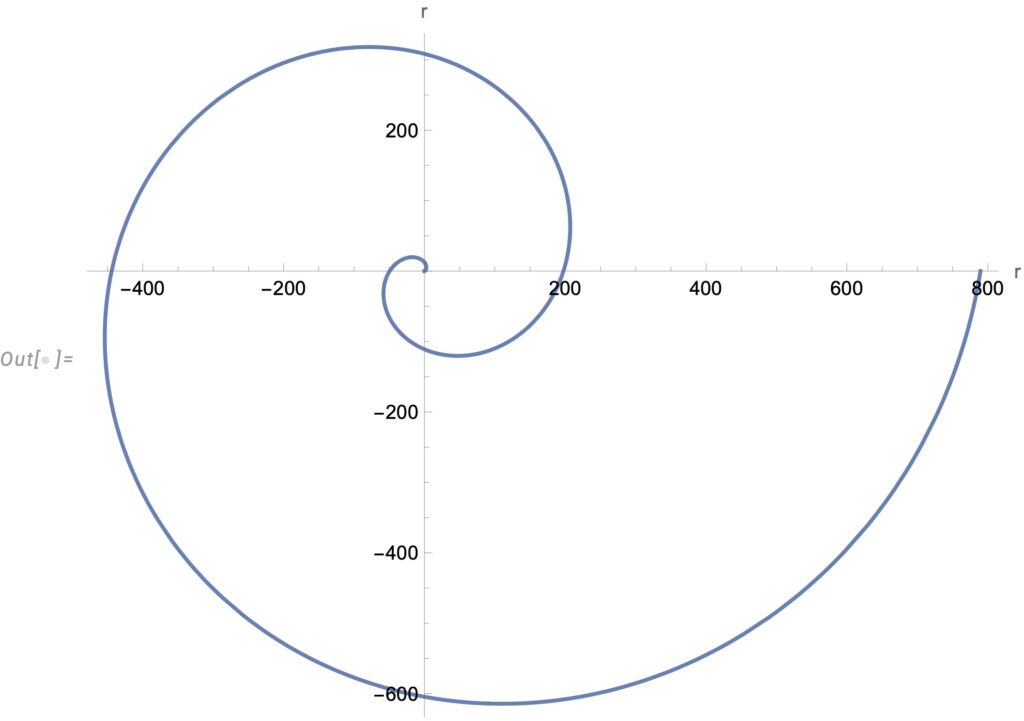
(풀이) 문제에 입자의 궤도식이 주어져 있으므로, 이를 활용해 \(u\), \(du/d\theta\), \(d^2 \theta/ d\theta^2\)을 구합니다.

\begin{align}
\tag{3-1}
u = {1 \over r} = {1 \over {c \theta^2}}
\end{align}

\begin{align}
\tag{3-2}
{{du}\over{d\theta}} =-2{1 \over c} \theta^{-3}
\end{align}

\begin{align}
\tag{3-3}
{{d^2 u}\over{d \theta^2}} &= 6 {1 \over c} \theta^{-4}\\[8pt]
&=6 {{c}\over{c^2 \theta^4}}\\[8pt]
&=6{c \over r^2}\\[8pt]
&=6cu^2
\end{align}

이제 (3-3)식을 (2-14)식 입자의 궤도방정식에 대입합니다.

\begin{align}
\tag{3-4}
6cu^2 + u = – {1 \over {ml^2 u^2}} f(u^{-1})
\end{align}

윗 식을 중심력에 대해 정리하면 다음과 같아요.

\begin{align}
\tag{3-5}
f(u^{-1}) = -ml^2u^2(6cu^2 + u)
\end{align}

마지막으로 구하고자 하는 중심력은 \(f(u^{-1})\)이 아닌 \(f(r)\)이므로 윗 식을 다음과 같이 \(r\)에 대한 함수로 되돌립니다.

\begin{align}
\tag{3-6}
f(r) = -ml^2 \Big({{6c}\over{r^4}} + {1 \over r^3}\Big)
\end{align}

결국 문제에 주어진 입자의 나선형 궤도를 형성하는 중심력은 바로 윗 식의 형태로 주어진다는 것을 알 수 있어요.