감쇠진동 미분방정식 예제 풀이

Last Updated on 2024-03-28 by BallPen

감쇠조화진동에 대한 미분방정식을 몇개 풀어보겠습니다.

감쇠진동 예제 몇개를 풀어보겠습니다.

감쇠진동은 감쇠조화진동이라고도 하고 감쇠조화운동이라고도 불러요. 우선 감쇠진동에 대한 복습부터 시작할게요. 그리고 미흡감쇠, 임계감쇠, 과다감쇠에 대한 예제를 다룹니다.

한번쯤 노트에 전체 풀이 과정을 스스로 정리해보는 것이 좋아요.

아래는 이번 글의 목차입니다.

1. 감쇠진동 복습

감쇠진동(감쇠조화운동, damped harmonic motion)에 대한 미분방정식은 다음과 같이 제차 이계 선형 상미분방정식으로 주어져요.

\tag{1-1}
{{d^2x}\over{dt^2}} + {c \over m} {dx \over dt} + {k \over m}x=0

여기서 x는 진동하는 물체의 변위, t는 시간, c는 저항력의 크기를 결정하는 감쇠계수, m은 진동하는 물체의 질량, k는 탄성력의 크기를 결정하는 용수철상수에요.

한편 단순조화진동에서 자연진동수 \omega_0는 다음과 같이 주어집니다.

\tag{1-2}
\omega_0 = \sqrt{k \over m}

또한 감쇠인자 \gamma를 다음 (1-3)식과 같이 정의할께요.

\tag{1-3}
\gamma = {c \over {2m}}

(1-2)식과 (1-3)식을 (1-1)식에 적용하면 다음과 같이 미분방정식의 모양을 바꾸어 표현할 수 있어요.

\tag{1-4}
{{d^2x}\over{dt^2}} + {2 \gamma} {dx \over dt} + {\omega_0^2}x=0

(1-4)식의 해는 다음과 같이 지수함수 꼴이 됩니다.

\tag{1-5}
x(t) = e^{ht}

그러므로 위 식에서 h만 구하면 (1-4)식에 주어진 미분방정식의 해를 완벽하게 구하는 거에요. 이를 위해 (1-5)식을 (1-4)식에 대입하여 정리하면 다음의 보조방정식을 얻을 수 있어요. 자세한 과정은 감쇠조화운동에 대한 이전 글을 참고해 주세요.

\tag{1-6}
h^2 + 2 \gamma h + \omega_0^2 = 0

보조방정식이 이차방정식이므로 근의 공식을 이용하면 다음과 같이 h를 구할 수 있어요.

\tag{1-7}
h = - \gamma \pm \sqrt{\gamma^2 - \omega_0^2}

이때 근호안에 있는 판별식이 양수인 경우 h는 두개의 실근, 0인 경우 중근, 음수인 경우 두개의 허근으로 주어지며, 이에 따라 (1-4)식의 미분방정식은 다음과 같이 세 종류의 일반해를 갖습니다.

1-1. 보조방정식이 두개의 실근을 갖는 경우: 과다감쇠

보조방정식이 두개의 실근을 갖는 경우 미분방정식의 일반해는 다음과 같습니다.

\tag{1-8}
x(t) = A e^{(-\gamma + q)t} + Be^{(-\gamma - q)t}

여기서 A와 B는 초기조건으로 결정되는 값이며, q는 \sqrt{\gamma^2 - \omega_0^2}을 뜻합니다.

(1-8)식으로 주어지는 감쇠진동을 ‘과다감쇠(또는 과도감쇠)’라고 해요.

1-2. 보조방정식이 중근을 갖는 경우: 임계감쇠

보조방정식이 중근을 갖는 경우 미분방정식의 일반해는 다음과 같습니다.

\tag{1-9}
x(t) = Ate^{-\gamma t} + B e^{-\gamma t}

여기서 A와 B는 초기조건으로 결정되는 값이에요.

(1-9)식으로 주어지는 감쇠진동을 ‘임계감쇠’라고 해요.

1-3. 보조방정식이 두개의 허근을 갖는 경우: 미흡감쇠

보조방정식이 두개의 허근을 갖는 경우 미분방정식의 일반해는 다음과 같습니다.

\tag{1-10}
x(t) = e^{-\gamma t} (A \cos \omega_d t + B \sin \omega_d t)

여기서 A와 B는 초기조건으로 결정되는 값이에요. 그리고 \omega_d는 감쇠과정에서 나타나는 진동자의 진동수인데요. \sqrt{\omega_0^2 - \gamma^2}로 구할 수 있어요.

(1-10)식으로 주어지는 감쇠진동을 ‘미흡감쇠’라고 해요.

이제 복습이 끝났으니 예제를 풀어보겠습니다.

2. 감쇠진동 예제 풀이

2-1. 예제1: 미흡감쇠

다음 미분방정식을 풀어 보세요. 이때 t=0인 순간에 변위는 x(0)=1이고, 속도는 v(0)=0입니다.

\tag{e1}
{{d^2 x}\over{dt^2}} + 0.2 {dx \over dt} + x = 0

(Sol) 일단 (e1)식과 (1-4)식을 비교하면 2 \gamma = 0.2이므로 \gamma = 0.1~\rm Hz가 됩니다. 또한 자연진동수는 \omega_0 = 1.0~\rm Hz임을 알 수 있어요.

그럼 보조방정식을 만들어봐요. 그러면 다음과 같아요.

\tag{e1-1}
h^2 + 0.2h +1 = 0

h를 구하기 위해 근의 공식을 적용해봐요.

\tag{e1-2}
\begin{align}
h &= {{-0.2 \pm \sqrt{0.2^2 - 4}}\over{2}}\\[10pt]
&={-0.1 \pm i 0.994987}
\end{align}

그결과 두개의 서로 다른 허근이 나왔어요. 이것은 주어진 미분방정식의 해가 미흡감쇠임을 의미하는 거에요.

그러면 (1-10)식을 이용해 미분방정식의 일반해를 구하면 됩니다.

[일반해]

미흡감쇠의 진동수 \omega_d는 \sqrt{\omega_0^2 - \gamma^2}으로 주어지므로 \omega_d = \sqrt{1.0^2 - 0.1^2} = 0.994987이 됩니다.

이 값들을 (1-10)식에 대입하면 다음과 같아요.

\tag{e1-2}
\begin{align}
x(t) &= e^{-\gamma t} (A \cos \omega_d t + B \sin \omega_d t)\\[0pt]
&=e^{-0.1t}(A\cos 0.994987t + B \sin 0.994987t)
\end{align}

위식이 바로 일반해 입니다. 만일 특수해를 구하고자 한다면 예제에 주어진 초기조건을 적용하여 A와 B를 구하면 됩니다.

[특수해]

문제에 주어진 t=0에서 변위 x(0)=1과, 속도 v(0)=0이 초기조건이에요. 일반해에 이 조건을 적용해봐요.

먼저 x(0)=1입니다. (e1-2)식의 t에 0을 대입하고 정리하면 됩니다.

\tag{e1-3}
\begin{align}
x(0) = e^{0}(A \cos 0 + B \sin0)&=1 \\[0pt]
A &=1
\end{align}

그 결과 A=1이 구해졌어요. (e1-2)식은 변위에 관한 식이므로, 이 식을 시간으로 한번 미분하면 속도가 됩니다. 미분을 해보면 다음과 같습니다.

\tag{e1-4}
\begin{align}
v(t) &= -0.1 e^{-0.1t} (A \cos 0.994987t + B \sin 0.994987)\\[0pt]
&~~~~~~~~~~~~~+e^{-0.1t} [-(0.994987)A\sin0.994987t + B(0.9984987)B\cos0.994987t]
\end{align}

그리고 t에 0을 대입하고 정리합니다.

\tag{e1-5}
\begin{align}
v(0) &= -0.1e^0 (A \cos0+B\sin 0 )\\[0pt]
&~~~~~~~~~~~+e^{0}[-(0.994987)A\sin0 + B(0.994987)\cos 0]\\[0pt]
&=-0.1A + B(0.994987)=0
\end{align}

이미 구한 A=1을 대입하고 정리하세요. 그러면 B는 다음과 같습니다.

\tag{e1-6}
B= 0.100504

결국 특수해는 다음과 같습니다.

\tag{e1-7}
\begin{align}
x(t)=e^{-0.1t}(\cos 0.994987t + (0.100504) \sin 0.994987t)
\end{align}

[미흡감쇠 그래프]

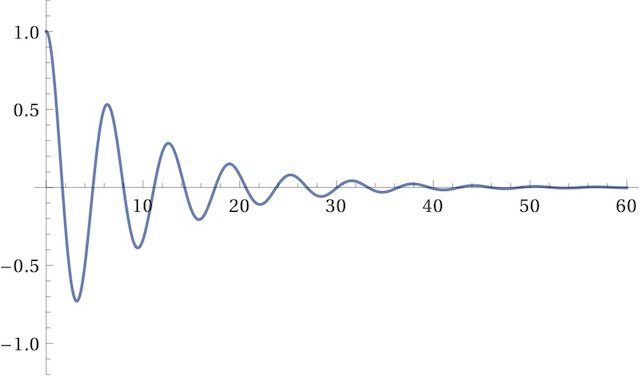
위에 있는 (e1-7)식의 그래프를 WolframAlpha로 그려보면 아래 [그림 1]과 같아요. 감쇠가 미흡하니 진동이 여러번에 걸쳐 일어나지만 결국에는 평형위치에 멈추는 것을 알 수 있어요.

참고로 그림을 그리는데 활용한 WolframAlpha 코드는 다음과 같아요.

plot (e^(-0.1t) (cos0.994987t + (0.100504)sin0.994987t)) t=0 to 60, y=-1.2 to 1.2

그래프를 보면 t=0에서 변위가 1.0으로 초기조건과 부합하는 것을 알 수 있어요.

2-2. 예제2: 임계감쇠

다음 미분방정식을 풀어보세요. 이때 t=0에서 변위는 x(0)=1.0이고, v(0)=0입니다.

\tag{e2}
{{d^2x}\over{dt^2}} + 2.0 {dx \over dt} + x =0

(Sol) 일단 (e2)식과 (1-4)식을 비교하면 2 \gamma=2.0 이므로 \gamma=1.0~\rm Hz가 됩니다. 또한 자연진동수는 \omega_0 = 1.0~\rm Hz임을 알 수 있어요.

한편 보조방정식은 다음과 같아요.

\tag{e2-1}
h^2 + 2.0 h +1 = 0

근의 공식을 적용해서 h를 구해 볼게요.

\tag{e2-2}
\begin{align}
h &= {{-2.0 \pm \sqrt{2.0^2 - 4}}\over{2}}\\[10pt]
&=-1.0
\end{align}

그 결과 h는 중근을 갖는다는 것을 알 수 있어요. 이것은 주어진 미분방정식의 해가 임계감쇠임을 의미합니다.

[일반해]

그러므로 (1-9)식의 일반해를 적용하세요.

\tag{e2-3}
\begin{align}
x(t) &= Ate^{- \gamma t} + Be^{- \gamma t}\\
&=A t e^{-1.0t}+Be^{-1.0t}\\
&=e^{-1.0t}(At+B)
\end{align}

여기서 A와 B는 초기조건으로 결정되는 값인데요.

이 값들을 구체적으로 결정하여 특수해를 구하고자 한다면 문제에 주어진 초기조건을 적용하면 됩니다.

[특수해]

문제에 주어진 t=0에서 변위 x(0)=1.0과 속도 v(0)=0이 초기 조건이에요. 이 조건을 적용해 봐요.

먼저 x(0)=1.0입니다.

\tag{e2-4}
\begin{align}
x(0)= e^0 (A0 + B)&=1.0\\
B&=1.0
\end{align}

B를 구했으니 이번에는 A를 구해봐요. 이를 위해 (e2-3)식을 시간으로 한번 미분한 후에 t 대신에 0을 대입하면 됩니다.

먼저 미분을 하면 다음과 같아요.

\tag{e2-5}
\begin{align}
v(t) = -1.0e^{-1.0t}(At+B)+e^{-1.0t}A
\end{align}

그리고 t에 0, B에 1.0을 대입하고 정리하여 A를 구합니다.

\tag{e2-6}
\begin{align}
v(0) = -1.0e^0(A0 + 1.0)+e^{0}A &= 0\\
A&=1.0
\end{align}

이제 위에서 구해진 A와 B를 (e2-3)식의 일반해에 대입하면 그게 바로 특수해입니다.

\tag{e2-7}
x(t) = e^{-1.0t}(t+1.0)

[임계감쇠 그래프]

WolframAlpha로 위 (e2-7)식의 그래프를 그려볼께요. 이때 사용한 코드는 참고로 다음과 같아요.

plot e^(-γt) (At+B) where (γ=1.0, A=1.0, B=1.0) t=0 to 60, y=-1.2 to 1.2

초기조건대로 t=0에서 물체의 변위가 1.0이며, 평형위치로 물체가 급격히 이동한 후 멈추게 됨을 이해할 수 있어요.

2-3. 예제3: 과다감쇠

다음 미분방정식을 풀어보세요. 이 경우에도 x(0)=1.0, v(0)=0입니다.

\tag{e3}
{{d^2x}\over{dt^2}} + 4.0 {dx \over dt} + x =0

(sol) (1-4)식과 비교하면 2 \gamma = 4.0이므로 \gamma=2.0~\rm Hz이고, 자연진동수는 \omega_0 = 1.0~\rm Hz입니다.

보조방정식은 다음과 같아요.

\tag{e3-1}
h^2 + 4.0 h +1 =0

근의 공식으로 h를 구하면 다음과 같습니다.

\tag{e3-2}
\begin{align}
h &= {{-4.0 \pm \sqrt{4.0^2 - 4}}\over{2}}\\[10pt]
&=-2.0 \pm \sqrt{3}
\end{align}

h가 서로 다른 두 실근을 갖는다는 것을 알 수 있어요. 이런 경우 운동은 과다감쇠가 됩니다.

[일반해]

(1-8)식을 이용해 일반해를 구해봐요. 이를 위해서는 q를 알아야 하는데요. q=\sqrt{\gamma^2 - \omega_0^2} = \sqrt{2.0^2 - 1.0^2}= \sqrt{3}이 되는군요.

결국 일반해는 다음과 같습니다.

\tag{e3-3}
\begin{align}
x(t) &= A e^{(-\gamma + q)t} + B e^{(-\gamma-q)t}\\
&=Ae^{(-2.0 + \sqrt{3})t} + B e^{(-2.0-\sqrt{3})t}
\end{align}

[특수해]

이번에는 특수해를 구해봐요. 이를 위해서는 초기조건을 적용하면 되죠. 먼저 첫번째 초기조건을 적용하면 다음과 같아요.

\tag{e3-4}
\begin{align}
x(0) = Ae^{0} + B e^0 &= 1.0\\
A&=1.0 - B
\end{align}

이번에는 두번째 초기조건을 적용하기 위해 (e3-3)식을 시간으로 한번 미분해서 속도에 관한 식으로 만들어봐요.

\tag{e3-5}
\begin{align}
v(t) = A(-2.0+\sqrt{3}) e^{(-2.0+\sqrt{3})t}+B(-2.0-\sqrt{3})e^{(-2.0-\sqrt{3})t}
\end{align}

그리고 v(0)=0이라는 초기조건을 적용합니다.

\tag{e3-6}
\begin{align}
v(0)&=A(-2.0+\sqrt{3})e^0 + B(-2.0-\sqrt{3})e^0\\
&=(1.0 -B)(-2.0+\sqrt{3}) + B(-2.0-\sqrt{3})=0\\
\end{align}

윗식을 정리하면 B는 다음과 같습니다.

\tag{e3-7}
B={{-2.0+\sqrt{3}}\over{2 \sqrt{3}}}

그리고 윗식을 (e3-4)식에 대입하여 A를 구하면 다음과 같아요.

\tag{e3-8}
A= {{2.0 + \sqrt{3}}\over{2\sqrt{3}}}

이제 초기조건에 의해 결정되는 A와 B를 모두 구했으니 일반해 (e3-3)식에 대입하여 정리합니다.

\tag{e3-9}
\begin{align}
x(t)&=Ae^{(-2.0 + \sqrt{3})t} + B e^{(-2.0-\sqrt{3})t}\\[10pt]
&={{2.0+\sqrt{3}}\over{2 \sqrt{3}}}e^{(-2.0+\sqrt{3})t} + {{-2+\sqrt{3}}\over{2 \sqrt{3}}}e^{(-2.0-\sqrt{3})t}\\[10pt]
&={1 \over 6}e^{(-2.0-\sqrt{3})t} \Big[(3+2\sqrt{3}) e^{2\sqrt{3}t}) + (3-2\sqrt{3}) \Big]
\end{align}

[과다감쇠 그래프]

WolframAlpha로 위 (e3-9)식을 그려볼께요. 이때 사용한 코드는 아래와 같습니다.

plot (Ae^((-2.0+Sqrt(3))t) + Be^((-2.0 - Sqrt(3))t)) where (A=((6.0+4 Sqrt(3))/(12)), B=((6.0-4 Sqrt(3))/(12))) t=0 to 60, y=-1.2 to 1.2

과다감쇠도 평형위치를 왔다 갔다하는 주기적 진동현상은 없어요. 얼핏보면 운동이 임계감쇠하고 비슷해 보이는데요. 감쇠가 크다보니 평형위치로 가는 시간이 임계감쇠보다 더 오래 걸립니다.

Related posts.

인공지능 기술 분야. 중소기업은 머신러닝 중심, 그럼 대기업은? 속력과 속도 – 속력과 속도를 구분하는 이유와 차이 관성의 크기는 질량이 결정한다. 오차 – 계통오차, 과실오차, 우연오차의 개념과 예시 소음도 가산과 감산 연습 문제 벡터의 뺄셈 : 벡터의 변화량을 구하는 도구 각운동 – 각속도와 접선속도, 각가속도와 접선가속도의 관계 중력 위치에너지 공식이 mgh인 이유