고유값 문제(eigenvalue problem)

BallPen · 2024-09-18T19:43:18+09:00

고유값 문제(eigenvalue problem)란 어떤 벡터를 정방행렬로 변환했을 때 결과 벡터가 원래 벡터의 실수배를 만족하는 경우, 실수배의 값을 행렬의 고유값, 원래 벡터를 고유값에 대응하는 고유벡터라고 합니다. 고유값 문제의 예제도 풀어보겠습니다.

Last Updated on 2024-09-18 by BallPen

행렬의 고유값, 고유벡터를 구하는 방법과 그 의미를 알아봐요.

고유값 문제(eigenvalue problem)란 어떤 입력 벡터 $\vec x$ 를 정방행렬 $A$ 로 변환했을 때 결과 벡터가 입력 벡터 $\vec x$ 의 실수배 $\lambda$ 를 만족하는 경우, $\lambda$ 를 행렬 $A$ 의 고유값, $\vec x$ 를 $\lambda$ 에 대응하는 고유벡터라고 합니다.

이를 식으로 표현하면 다음과 같아요.

\tag{D1} A \vec x = \lambda \vec x

고유값 문제란 위 식을 만족하는 고유값 $\lambda$ 와 고유벡터 $\vec x$ 를 구하는 구하는 것을 말해요.

그럼 이제부터 고유값 문제 해법과 그 의미를 구체적으로 알아봐요.

아래는 이번 글의 목차입니다.

Contents

1. 고유값 문제
- 1-1. 정의
- 1-2. 고유값 문제 의미
2. 고유값 문제 풀이 방법
- 2-1. 고유값
- 2-2. 고유벡터
3. 고유값 문제 예제 : 고유벡터의 직교성

이 글에서 사용된 그림 파일은 아래 링크에서 다운 받으세요. 맥의 키노트로 작성되었어요.

맥 키노트 파일: eigenvalue_problem.key

1. 고유값 문제

1-1. 정의

일반적으로 벡터 $\vec x$ 에 선형 변환 정방행렬 $A$ 를 취하면 다른 벡터 ${\vec x}~^{\prime}$ 가 나옵니다. 식으로 쓰면 다음과 같아요.

\tag{1-1} A \vec x = \vec x~^{\prime}

이때 결과 벡터 $\vec x^{\prime}$ 은 입력 벡터 $\vec x$ 와는 서로 다른 방향과 크기를 갖게 됩니다.

하지만 어떤 벡터 $\vec x$ 는 다음의 경우를 만족하기도 해요.

\tag{1-2} A \vec x = \lambda \vec x

즉 어떤 벡터 $\vec x$ 를 행렬 $A$ 로 변환했을 때 원래 벡터 $\vec x$ 의 $\lambda$ 실수배로 나오는 거에요. 즉 변환 전 입력 벡터와 변환 후 결과 벡터의 방향이 보존되는 경우가 있다는 거에요.

이때 $\lambda$ 를 행렬 $A$ 의 고유값, $\vec x$ 를 $\lambda$ 에 대응하는 고유벡터라고 합니다.

고유값 문제란 바로 (1-2)식의 조건을 만족하는 고유벡터 $\vec x$ 와 고유값 $\lambda$ 를 구하는 것을 말해요.

1-2. 고유값 문제 의미

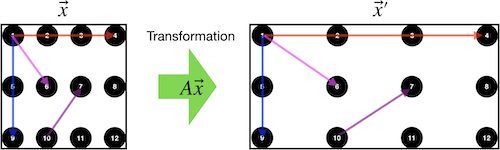
아래 [그림 1]의 왼쪽을 보면 검정색 정사각형이 있고, 그 안에 총 12개의 점이 있어요. 그런데 그 정사각형을 가로로 2배, 세로로 1배 확대하는 변환행렬 $A$ 를 취했더니 오른쪽 그림과 같이 직사각형으로 바뀌었어요.

[그림 1] 고유값 문제 의미. 벡터 <span class="katex-eq" data-katex-display="false">\vec x</span>에 변환을 취하여 <span class="katex-eq" data-katex-display="false">A \vec x</span>를 해주면 <span class="katex-eq" data-katex-display="false">\vec x~^ \prime</span>가 됩니다. 이때 빨강색과 파랑색 벡터는 <span class="katex-eq" data-katex-display="false">A\vec x = 2 \vec x</span>와 <span class="katex-eq" data-katex-display="false">A \vec y = 1 \vec y</span>를 만족합니다. — [그림 1] 고유값 문제 의미. 벡터 $\vec x$ 에 변환을 취하여 $A \vec x$ 를 해주면 $\vec x~^ \prime$ 가 됩니다. 이때 빨강색과 파랑색 벡터는 $A\vec x = 2 \vec x$ 와 $A \vec y = 1 \vec y$ 를 만족합니다.

이때 왼쪽 정사각형 안에 있던 점도 오른쪽 그림의 위치로 바뀌게 될 것을 상상할 수 있을 거에요.

그림에서 1번 점을 원점이라고 했을 때 1번에서 4번을 향하는 빨강색 벡터와 1번에서 9번을 향하는 파랑색 벡터는 변환 전과 후에 벡터의 크기는 다를지라도 방향은 그대로 보존됨을 알 수 있어요.

이를 식으로 쓰면 다음 관계가 성립합니다. 이때 변환 전의 빨강색 벡터를 $\vec x$ 라 하고, 파랑색 벡터는 $\vec y$ 라고 할게요.

\tag{1-3} \begin{align} &A \vec x = 2 \vec x\\ &A \vec y = 1 \vec y \end{align}

하지만 이 두벡터를 제외하고 1번에서 6번을 향하는 자주색 벡터와 10번에서 7번을 향하는 보라색 벡터 들은 모두 크기와 방향이 달라졌음을 알 수 있어요.

따라서 빨강색과 파랑색의 두 벡터만이 (1-2)식의 고유값 문제를 만족하고, 이때 2와 1을 행렬 $A$ 의 고유값이라고 합니다. 물론 $\vec x$ 와 $\vec y$ 는 고유벡터가 되는 거에요.

2. 고유값 문제 풀이 방법

그렇다면 고유값 문제를 어떻게 풀어내는지 그 방법을 알아봐요.

2-1. 고유값

먼저 고유값 $\lambda$ 를 구해봐요.이를 위해서는 우선 (1-2)식의 우변을 좌변으로 이항해봐요.

\tag{2-1} (A \vec x - \lambda {\color{red}\vec x}) =0

그리고 위 식에서 빨강색 벡터의 좌측에 단위행렬 $I$ 를 곱해도 식은 여전히 성립하죠.

\tag{2-2} (A \vec x - \lambda {\color{red}I\vec x}) =0

이때 단위벡터를 곱하는 이유는 벡터 $\vec x$ 를 공통인수로 밖으로 빼내려고 하는 거에요. 그러면 아래 식과 같이 괄호안의 수식을 행렬연산으로 묶을 수 있어요.

\tag{2-3} (A - \lambda I)\vec x =0

이때 중요한 것은 $\vec x \ne 0$ 조건하에서 위 식이 성립하도록 하는 어떤 조건이 필요해요. 이를 위해 위 (2-3)식의 양변에 $A - \lambda I$ 의 역행렬을 취해봐요.

\tag{2-4} \begin{align} (A - \lambda I)^{-1} (A - \lambda I) \vec x &= (A-\lambda I)^{-1}0\\[5pt] I\vec x &= 0 \\ \vec x&=0 \end{align}

그 결과 위 식과 같이 $\vec x$ 가 0이 되어서는 안되는데, $\vec x = 0$ 이 되는 모순적 결과가 얻어져요. 그러므로 $A - \lambda I$ 의 역행렬이 존재해서는 안됩니다.

이때 역행렬이 존재하지 않기 위해서는 $A - \lambda I$ 의 행렬식이 0이 되어야 해요.

\tag{2-5} |A-\lambda I | =0

예를 들어 3×3 변환 행렬을 가정했을 때 (2-5)식은 다음과 같아요.

\tag{2-6} \begin{vmatrix} \begin{pmatrix} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33} \end{pmatrix} -\lambda \begin{pmatrix} 1 &0 & 0\\ 0 & 1 & 0\\ 0 & 0& 1 \end{pmatrix} \end{vmatrix} =0

그리고 위 식을 정리하면 다음과 같죠.

\tag{2-7} \begin{vmatrix} a_{11} - \lambda & a_{12} & a_{13} \\ a_{21} & a_{22}-\lambda & a_{23}\\ a_{31} & a_{32} & a_{33}-\lambda \end{vmatrix} =0

위 (2-7)식의 행렬식을 구하면 $\lambda$ 의 3차 방정식이 나올거에요. 그리고 그것을 풀면 고유값인 $\lambda$ 를 구할 수 있습니다.

2-2. 고유벡터

그렇다면 고유벡터는 어떻게 구하면 될까요?

이미 고유값 $\lambda$ 를 구했으니 그 값을 (1-2)식에 대입하여 고유벡터의 각 성분을 구하면 됩니다.

3. 고유값 문제 예제 : 고유벡터의 직교성

변환행렬 $A$ 가 다음과 같을 때 고유값과 고유벡터를 구해 보세요. 또한 각 고유벡터 사이의 직교 여부를 판정해보세요.

\tag{3-1} A= \begin{pmatrix} 2 & 0 & -1\\ 0 & 2 & 0\\ -1 & 0 &2 \end{pmatrix}

3-1. 고유값

우선 고유값을 구하기 위해서는 (2-5)식인 $|A-\lambda I|=0$ 을 적용하면 됩니다.

\tag{3-2} \begin{vmatrix} \begin{pmatrix} 2 & 0 & -1\\ 0 & 2 & 0\\ -1 & 0 & 2 \end{pmatrix} -\lambda \begin{pmatrix} 1 &0 & 0\\ 0 & 1 & 0\\ 0 & 0& 1 \end{pmatrix} \end{vmatrix} =0

위 식을 정리하면 다음과 같아요.

\tag{3-3} \begin{align} \begin{vmatrix} 2-\lambda & 0 & -1\\ 0 & 2- \lambda & 0\\ -1 & 0 & 2-\lambda \end{vmatrix} &=(2 - \lambda)^3-(2-\lambda)\\ &=(2 - \lambda)[(2-\lambda)^2 -1]\\ &=(2-\lambda)(\lambda^2 -4 \lambda +3)\\ &=(2-\lambda)(\lambda -3)(\lambda -1) =0 \end{align}

따라서 위 식이 성립되기 위해서는 $\lambda =2$ 또는 $\lambda = 3$ 또는 $\lambda =1$ 이 만족되어야 합니다.

즉, 세개의 고유값이 구해지는데요. 크기순서로 $\lambda_1 =1$ , $\lambda_2 = 2$ , $\lambda_3 =3$ 으로 정하겠습니다.

3-2. 고유벡터

그럼 이제부터는 고유값에 대응하는 고유벡터를 구해봐요.

[고유값 = 1인 경우]

먼저 고유값 $\lambda_1 =1$ 인 경우에 대한 고유 벡터 $\vec x_1$ 이에요.

이를 위해 고유값을 $A \vec x = \lambda \vec x$ 인 (1-2)식에 대입해보세요. 그러면 아래와 같습니다.

\tag{3-4} \begin{pmatrix} 2 & 0 & -1 \\ 0 & 2 &0\\ -1 & 0 & 2 \end{pmatrix} \begin{pmatrix} x_1\\ x_2\\ x_3 \end{pmatrix} =1 \begin{pmatrix} x_1\\ x_2\\ x_3 \end{pmatrix}

이제 위 식을 전개한 후 연립하여 풀어 벡터 $\vec x_1$ 의 각 성분 $x_1,~x_2,~x_3$ 을 구하면 됩니다. 여기서 $\vec x_1$ 는 고유벡터를, $x_1$ 은 고유벡터 $\vec x_1$ 의 한 성분을 나타냅니다. 헷갈리지 마셔요.

\tag{3-5} \left \{ \begin{align*} &2x_1 - x_3 = x_1\\ &2 x_2 = x_2\\ &-x_1 + 2x_3 = x_3 \end{align*} \right.

그 결과 $x_1 = x_3$ 를 만족하는 임의값 $a$ 면 되고, $x_2 =0$ 임을 알 수 있어요.

따라서 $\lambda_1 = 1$ 에 대응하는 고유 벡터 $\vec x_1$ 은 다음과 같습니다.

\tag{3-6} \begin{align} \vec x_1 = \begin{pmatrix} a \\ 0\\ a \end{pmatrix} =a \begin{pmatrix} 1\\ 0\\ 1 \end{pmatrix} \end{align}

이때 위 식에서 $a$ 는 아무 값이나 대입되어도 성립하지만, 고유벡터의 크기가 1이 되도록 벡터 정규화(vector normalization)를 하는 것이 일반적입니다.

이를 위해서는 행렬 안의 성분이 1, 0, 1이므로 이 벡터의 크기는 다음과 같을 거에요.

\tag{3-7} \begin{align} \sqrt{1^2 + 0^2 + 1^2} = \sqrt{2} \end{align}

그 결과 $\sqrt{2}$ 가 나오는데요. 이 값의 역수를 $a$ 로 정하면 고유벡터 $\vec x_1$ 의 크기는 1로 정규화됩니다.

그러므로 고유값 $\lambda_1 =1$ 에 대응하는 고유벡터 $\vec x_1$ 은 다음과 같습니다.

\tag{3-8} \vec x_1 = {1 \over {\sqrt{2}}} \begin{pmatrix} 1\\ 0\\ 1\\ \end{pmatrix}

[고유값 = 2인 경우]

이번에는 고유값 $\lambda_2 = 2$ 인 경우에 대한 고유벡터 $\vec x_2$ 를 구해봐요.

먼저 고유값을 $A \vec x = \lambda \vec x$ 에 대입하세요.

\tag{3-9} \begin{pmatrix} 2&0&-1\\ 0&2&0\\ -1&0&2 \end{pmatrix} \begin{pmatrix} x_1\\ x_2\\ x_3 \end{pmatrix} =2 \begin{pmatrix} x_1\\ x_2\\ x_3 \end{pmatrix}

그리고 위 식을 전개해서 고유벡터의 각 성분을 구하세요.

\tag{3-10} \left \{ \begin{align*} &2 x_1 - x_3 = 2 x_1\\ &2 x_2 = 2x_2\\ &-x_1 + 3x_3 = 2 x_3 \end{align*} \right.

그러면 $x_1$ 은 0이며 $x_2$ 는 임의의 숫자 $a$ 이면 되고, $x_3$ 는 0이 되어야 함을 알 수 있어요.

따라서 $\lambda_2=2$ 에 대응하는 고유벡터 $\vec x_2$ 는 다음과 같습니다.

\tag{3-11} {\vec x_2 = \begin{pmatrix} 0\\ a\\ 0\\ \end{pmatrix} = a \begin{pmatrix} 0\\ 1\\ 0\\ \end{pmatrix}}

이번에도 벡터 $\vec x_2$ 의 크기가 1이 되도록 벡터정규화를 하면 되는데요. 각 성분의 크기가 0, 1, 0이므로 벡터의 크기는 아래와 같이 1이 됩니다.

\tag{3-12} \sqrt{0^2 + 1^2 + 0^2} =1

그러므로 이 값의 역수도 1이므로 (3-11)식의 $a$ 를 1로 두면 됩니다.

결국 고유값 $\lambda_2=2$ 에 대응하는 고유벡터 $\vec x_2$ 는 다음과 같습니다.

\tag{3-13} \vec x_2 = \begin{pmatrix} 0\\ 1\\ 0\\ \end{pmatrix}

[고유값 = 3인 경우]

이번에는 고유값 $\lambda_3=3$ 인 경우에 대한 고유벡터 $\vec x_3$ 입니다. 먼저 고유값을 $A \vec x = \lambda \vec x$ 에 대입하세요.

\tag{3-14} \begin{pmatrix} 2&0&-1\\ 0&2&0\\ -1&0&2 \end{pmatrix} \begin{pmatrix} x_1\\ x_2\\ x_3 \end{pmatrix} =3 \begin{pmatrix} x_1\\ x_2\\ x_3 \end{pmatrix}

그리고 윗 식을 전개해서 고유벡터의 각 성분을 구하면, $x_1=-x_3$ 을 만족하는 임의의 값 $a$ 이면 되고, $x_2=0$ 이 되어야 합니다.

결국 $\lambda_3=3$ 에 대응하는 고유벡터 $\vec x_3$ 는 다음과 같습니다.

\tag{3-15} \begin{align} \vec x_3 = \begin{pmatrix} a\\ 0\\ -a\\ \end{pmatrix} = a \begin{pmatrix} 1\\ 0\\ -1\\ \end{pmatrix} \end{align}

그리고 벡터 정규화를 하면 $a={1 \over \sqrt{2}}$ 이 되어야 벡터 $\vec x_3$ 의 크기가 1이 됩니다.

따라서 $\lambda_3=3$ 에 대응하는 고유벡터 $\vec x_3$ 는 다음과 같습니다.

\tag{3-16} \vec x_3 = {1 \over \sqrt{2}} \begin{pmatrix} 1\\ 0\\ -1\\ \end{pmatrix}

3-3. 고유벡터의 직교성

지금까지 주어진 행렬 $A$ 에 대한 고유값과, 그 고유값에 대응하는 고유벡터들을 아래와 같이 구했어요.

\tag{3-17} \vec x_1 = {1 \over \sqrt{2}} \begin{pmatrix} 1\\ 0\\ 1\\ \end{pmatrix} ,~~~\vec x_2 = \begin{pmatrix} 0\\ 1\\ 0\\ \end{pmatrix} ,~~~\vec x_3= {1 \over \sqrt{2}} \begin{pmatrix} 1\\ 0\\ -1\\ \end{pmatrix}

그런데 이 벡터들은 서로 수직한 특성을 갖고 있는 것으로 알려져 있어요. 그래서 이번에는 이 벡터들의 직교성에 대해 알아보겠습니다.

우선 각 벡터 화살표를 매스매티카로 그려보면 [그림 2]와 같습니다. 참고로 매스매티카 코드는 아래를 참고해주세요.

벡터들 사이의 직교성을 알기 위해서는 벡터의 내적을 활용하면 돼요. 만일 두 벡터가 서로 직교한다면 벡터의 내적은 0이 될거에요.

먼저 첫번째와 두번째 고유벡터 사이의 내적입니다.

\tag{3-18} \begin{align} \vec x_1 \cdot \vec x_2 &= {x_1}^T x_2\\ &={1 \over \sqrt{2}} \begin{pmatrix} 1&0&1 \end{pmatrix} \begin{pmatrix} 0\\ 1\\ 0 \end{pmatrix}\\ &=0 \end{align}

이번에는 두번째와 세번째 고유벡터 사이의 내적입니다.

\tag{3-19} \begin{align} \vec x_2 \cdot \vec x_3 &= {x_2}^T x_3\\ &= \begin{pmatrix} 0&1&0 \end{pmatrix} \begin{pmatrix} 1\\ 0\\ -1 \end{pmatrix} {1 \over \sqrt{2}}\\ &=0 \end{align}

같은 방식으로 첫번째와 세번째 고유벡터 사이의 내적입니다.

\tag{3-20} \begin{align} \vec x_1 \cdot \vec x_3 &= {x_1}^T x_3\\ &= {1 \over \sqrt{2}} \begin{pmatrix} 1&0&1 \end{pmatrix} \begin{pmatrix} 1\\ 0\\ -1 \end{pmatrix} {1 \over \sqrt{2}}\\ &=0 \end{align}

그 결과 모든 고유벡터 사이의 내적이 0이므로 서로 직교함을 알 수 있어요.

흥미롭고 도움이 되는 글이었나요? 리뷰를 부탁드립니다.

[Total: 1 Average: 5]