Last Updated on 2024-01-06 by BallPen
로그 계산을 위한 기본 성질과 로그가 활용된 사례를 알아보겠습니다. 의외로 로그는 활용도가 높아요.
로그 성질과 활용 사례를 이번 글에서 다루고자 합니다.
John Napier(1550~1617)가 발명한 로그(log, logarithm)는 다양한 분야에서 활용되고 있어요. 함께 알아봐요.
아래는 이번 글의 목차입니다.
Contents
1. 로그 정의
1-1. 지수함수의 역함수
로그함수란 지수함수의 역함수를 말합니다.
– 로그함수의 정의
아래 (1)식의 함수가 있다고 보세요. 이 함수는 x값을 입력받아 y값을 구하는 거에요.
\tag{1}
\begin{align}
y=x+1
\end{align}그런데 이 함수를 변경하여 y값을 입력받아 x값을 계산하고 싶으면 우리는 다음과 같이 식을 바꿀것입니다.
\tag{2}
\begin{align}
x &=y-1
\end{align}그리고는 보통 입력되는 값을 x라 하고, 결과 값을 y라고 하니 x와 y의 기호를 서로 바꾸어 다음과 같이 최종 표기합니다.
\tag{3}
y=x-1이와 같이 입력값과 결과값의 일대일 관계를 서로 바꾸어 놓은 함수를 원래함수의 역함수라고 우리는 보통 부르게 됩니다. 즉 (1)식이 원래함수이고, (2)식이 (1)식의 역함수인 거에요.
그렇다면 y = 10^x인 지수함수가 있다고 생각해봐요. 여기서 용어를 몇가지만 정리하고 가겠습니다. 이 식에서 y는 진수, 10은 밑, x를 지수라고 부릅니다.
이 함수의 역함수는 어떻게 구할 수 있을까요? 바로 (1)식과 (2)식의 방법을 그대로 적용해 보겠습니다.
\tag{4}
\begin{align}
y&=10^x\\
10^x &= y
\end{align}(3)식의 두번째 줄을 x에 관해 정리하면 되는데, 이때 사용되는 것이 로그 \log입니다. 바로 다음과 같이 \log기호를 사용하는 것이죠.
\tag{5}
\begin{align}
x={\log_{10}} y
\end{align}그리고는 x와 y의 기호를 아래 (6)식과 같이 서로 바꾸면 (4)식의 지수함수에 대한 역함수가 구해지는 것입니다.
\tag{6}
y={\log_{10}}x여기에서도 용어는 지수함수의 용어를 그대로 사용합니다. 물론 함수의 모양을 일반화하기 위해 x와 y의 기호는 서로 바꾸었지만요. (6)식에서 10을 밑, x를 진수라고 합니다. 결국 로그 함수는 지수 함수에서의 지수 y값을 구하는 함수로 보면 됩니다.
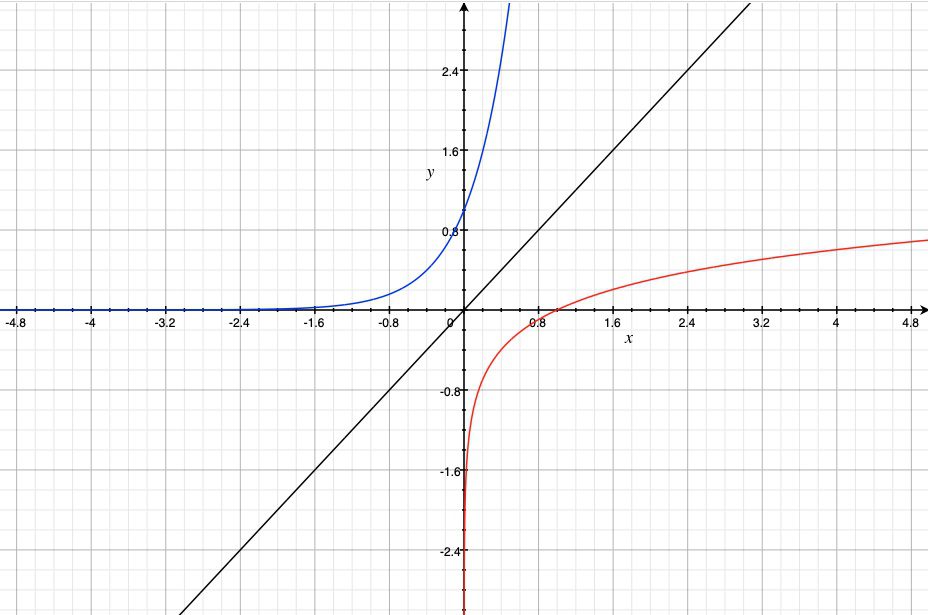
위에서 말씀드렸듯이 지수함수와 로그함수는 서로 역함수 관계입니다. 아래 [그림 1]에서 파랑색 곡선은 y=10^x의 그래프이고 빨강색 곡선은 y={\log_{10}}x의 그래프입니다. 이 두 곡선이 y=x 그래프에 대해 대칭인 것을 알 수 있습니다.
![[그림 1] 로그함수는 지수함수의 역함수입니다. 파랑색 곡선이 지수함수이고 빨강색 곡선이 로그함수입니다. 이 두 곡선은 <span class="katex-eq" data-katex-display="false">y=x</span>인 검정색 곡선에 대해 서로 대칭의 관계를 갖습니다.](https://ballpen.blog/wp-content/uploads/2021/12/Screen-Shot-2021-12-10-at-9.39.29-PM.png)
– 다양한 로그 함수 : 상용로그와 자연로그
또 하나 중요한 것은 밑이 항상 10일 필요는 없다는 것입니다. 일반적으로 밑이 10인 경우가 일상생활에서 많이 사용되기 때문에 이를 상용로그라고 합니다. 그래서 상용로그의 \log_{10}을 줄여 그냥 \log로 표현을 많이 합니다.
밑은 0보다 크고 1이 아닌 수면 무엇이든 가능합니다. 예를 들어 아래와 같은 경우가 모두 가능합니다.
- y=2^x~\longleftrightarrow x={\log_2}y \longleftrightarrow y={\log_2}x
- y=e^x~\longleftrightarrow x={\log_e}y \longleftrightarrow y={\log_e}x
위 예시에서 밑이 오일러상수 e인 경우에 대해서 제시했는데요. 이러한 로그함수는 자연계를 기술하는 수학에서 자주 등장하게 됩니다. 그래서 이 로그함수를 특별히 자연로그라고 합니다. 그리고 \log_e 기호 대신에 ln으로 바꾸어 표기하는 경우가 많아요.
1-2. 예제 풀이
아주 간단한 경우를 예로 들어 보겠습니다.
(예제1) 10^{y} = 2.10으로 주어진 관계가 있습니다. y가 얼마가 되면 이 식의 관계가 성립할까요?
(Sol) 밑이 10이고 진수가 2.10을 만족하는 지수 값 y를 구하는 문제입니다. 이때 필요한 것이 로그입니다.
\tag{7}
\begin{align}
10^y &=2.10\\
y &={\log_{10}}{2.10}
\end{align}이때 한 가지 문제가 있는데요. (6)식에서 두번째 줄의 우변이 무슨 값을 갖느냐 입니다. 이때 사용하도록 편리하게 만든 표가 로그표입니다. 또는 계산기로도 쉽게 계산되는데요. {\log_{10}}{2.10}을 계산기로 확인해보면 0.3222가 나옵니다.
결국 (7)식의 첫번째 줄이 성립하기 위한 y값이 0.3222가 된다는 것입니다.
2. 로그의 기본 성질
로그 계산 과정에서 자주 사용되는 몇 가지 기본 성질이 있습니다. 이에 대한 정의와 증명을 알아보겠습니다. 여기에서는 밑이 10인 상용로그를 예로 들었는데요. 밑은 위에서 설명한 바와 같이 1이 아닌 양의 값이면 모두 가능합니다. 밑은 2, e, 5, 7 등 다른 숫자로 바꿀 수 있다는 것을 꼭 기억하세요.
2-1. 로그의 성질 #1
{\log_{10}}1 = 0
{\log_{10}}10 = 1
(증명) 10^0 = 1이고, 10^1 = 10입니다. 이것을 (4)와 (5)식의 역함수 관계를 적용하면 {\log_{10}}1 =0이고, {\log_{10}}10 = 1이 됩니다.
2-2. 로그의 성질 #2
{\log_{10}}(M \times N)~=~{\log_{10}}M+{\log_{10}}N
(증명) 10^x = M이고, 10^y = N으로 주어진 지수함수를 생각해 보세요. 그리고 이 두 지수함수의 역함수를 각각 구하면 x= {\log_{10}}M이고 y = {\log_{10}}N이 됩니다.
이번에는 두 지수함수를 곱해 볼까요. 그러면 10^x \times 10^y = 10^{x+y} = M\times N의 관계가 성립합니다. 이때 이 식에서 두번째와 세번째 항의 식에 대한 역함수를 구하면 {\log_{10}}{(M \times N)} = x+y ={\log_{10}}M + {\log_{10}}N이 성립하게 됩니다.
2-3. 로그의 성질 #3
{\log_{10}}({{M}\over{N}})~=~{\log_{10}}M-{\log_{10}}N
(증명) 이번에도 10^x = M이고, 10^y = N으로 주어진 지수함수를 생각해 보세요. 그리고 이 두 지수함수의 역함수를 각각 구하면 x= {\log_{10}}M이고 y = {\log_{10}}N이 됩니다.
이번에는 이 두 지수함수를 나누어 볼까요. 그러면 {{10^x} / {10^y}}=10^x \times (10^y )^{-1} = 10^x \times 10^{-y} = 10^{x-y} = {{M}\over{N}}의 관계가 성립합니다.
이때 위 관계에서 네번째와 다섯번째 항의 식에 대한 역함수를 구하면 {\log_{10}}{({{M}\over{N}})} = x-y ={\log_{10}}M - {\log_{10}}N이 성립하게 됩니다.
2-4. 로그의 성질 #4
k{\log_{10}}L = {\log_{10}}L^k
(증명) 10^x = M=L^k의 관계가 성립한다고 보겠습니다. 즉 임의의 x에 대한10^x의 값 M이 L의 k제곱으로 주어지는 것이죠.
그러면 위 관계에서 첫번째와 세번째 항에 대한 역함수를 구하면 x={\log_{10}}L^k가 성립합니다.
또한 첫번째와 세번째 항의 관계가 10^x = L^k이므로, 양변을 1/k제곱하면 (10^x)^{1/k} = (L^k)^{1/k}이 됩니다. 이 식을 정리하면 10^{x/k} = L이 되며, 이 관계의 역함수를 구하면 {\log_{10}}L = x/k가 됩니다.
그리고 {\log_{10}}L = x/k의 양변을 k로 곱하면 k{\log_{10}}L = x ={\log_{10}}L^k이 성립하게 됩니다.
3. 로그 활용 사례
3-1. 음압레벨과 등가소음도
소음의 음압레벨(Sound Pressure Level)이나 등가소음도(Equivalent Noise Level)에서 로그 함수가 사용됩니다. 이에 대해서는 아래 링크를 클릭하시면 사용되는 사례를 구체적으로 볼 수 있어요.
- 음압 레벨과 등가소음도 (클릭)
3-2. 차이가 아주 큰 값 들을 하나의 그래프에서 표현할 때
로그는 아주 작은 수와 아주 큰 수가 섞여있는 데이터를 그래프로 표현할 때에도 유용하게 사용됩니다.
아래 표에 있는 데이터는 여러분들이 실험을 통해 측정한 값이라고 생각해보세요. 이것을 그래프로 나타내고자 합니다.
| x값 | y값 |
|---|---|
| 0 | 2 |
| 1 | 1 |
| 2 | 4 |
| 3 | 2 |
| 4 | 1000 |
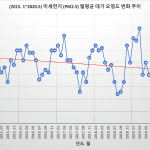
통상적인 꺽은선 그래프를 그려보면 아래 [그림 2]와 같은 모양으로 그려지게 됩니다. 문제는 (4,1000) 좌표의 데이터에 의해 아주 작은 (0,2), (1,1), (2,4), (3,2)의 y좌표가 명확하게 보이지 않고 거의 0으로 그려진다는 것입니다.
![[그림 2] 아주 큰 값에 의해 아주 작은 <span class="katex-eq" data-katex-display="false">y</span>값이 거의 0으로 그려지게 됩니다.](https://ballpen.blog/wp-content/uploads/2021/12/Screen-Shot-2021-12-10-at-10.40.57-PM-1024x680.png)
이렇게 그래프를 그리면 표에 담겨진 데이터의 세부 정보를 다른 사람들에게 전달하는데 실패하게 되는 것이죠.
그렇다면 어떻게 해야 아주 큰 데이터에서 작은 데이터까지 하나의 그래프에 모두 명확하게 보여줄 수 있을까요? 바로 y축을 로그눈금으로 그리면 가능합니다.
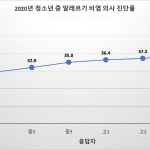
![[그림 3] <span class="katex-eq" data-katex-display="false">y</span>축을 로그 눈금으로 바꾸게 되면 아주 작은 데이터와 큰 데이터를 하나의 그래프에 모두 그릴 수 있습니다.](https://ballpen.blog/wp-content/uploads/2021/12/Screen-Shot-2021-12-10-at-10.54.41-PM-1024x680.jpg)
[그림 3]은 표의 데이터를 꺽은선 그래프로 그려낸 것인데요. [그림 2]와의 차이점은 y축의 눈금을 로그 눈금(또는 대수 눈금이라 부름)으로 바꾸었다는 것입니다.
그림과 같이 아주 작은 데이터에서부터 아주 큰 데이터까지 모두 명확하게 보여지는 것을 알 수 있습니다.
로그는 정말 유용한 것 같아요.
4. 로그의 기본 성질과 활용 사례 요약
- 로그함수는 지수함수의 역함수이다. 그러므로 두 함수의 그래프는 y=x에 대하여 대칭이다.
- 밑이 10인 상용로그는 보통 log로 표기하며, 밑이 오일러상수 e인 자연로그는 보통 ln으로 표기한다.
- 로그는 4개의 기본성질을 갖는다.
- 로그는 대표적으로 소음과 진동 분야에서 두루 쓰이며, 아주 작은 수치의 데이터와 큰 수치의 데이터를 하나의 그래프에 모두 표현하고자 할 때 사용될 수 있다.