방향코사인 정의와 의미

by

Last Updated on 2024-03-04 by BallPen

단위벡터로부터 방향코사인의 정의와 의미를 알아보겠습니다.

방향코사인 (direction cosine)이란 단위 벡터를 양의 xx축, 양의 yy축, 양의 zz축으로부터의 각도를 이용하여 표기하는 또 하나의 방법을 말합니다.

기초적인 삼각함수만 알고 있으면 아주 쉽게 이해할 수 있어요.

아래는 이번 글의 목차입니다.

1. 단위 벡터

방향코사인 개념을 이해하기 위해서는 우선 벡터와 단위 벡터를 알아야 합니다. 이에 대해 간단히 복습을 해보겠습니다.

1-1. 벡터

벡터는 기본적으로 크기와 방향을 갖는 양입니다.

예를 들어 3.0x^3.0 \hat x의 벡터가 있을 때 3.0은 벡터의 크기이고 x^\hat x는 벡터의 방향이 xx방향임을 나타냅니다.

같은 방식으로 yy방향으로 크기가 4.0인 벡터는 4.0y^4.0 \hat y로, zz방향으로 크기가 5.0인 벡터는 5.0z^5.0 \hat z로 표기하죠.

벡터는 서로 합해질 수 있어요. 그것을 벡터의 덧셈이라 합니다.

위에서 예로 들었던 세 벡터를 하나로 합해 볼까요. 합해진 벡터를 A⃗\vec A라고 한다면 아래 (1)식과 같이 표기할 수 있어요.

A⃗=Axx^+Ayy^+Azz^=3.0x^+4.0y^+5.0z^(1)\tag{1} \begin{align} \vec A &= A_x \hat x + A_y \hat y + A_z \hat z \\[7pt] &=3.0\hat x + 4.0 \hat y + 5.0 \hat z\\ \end{align}

또한 (1)식으로 주어진 벡터를 그림으로 나타내면 아래 [그림 1]의 검정색 화살표로 표현할 수 있습니다.

[그림 1] (1)식에 주어진 벡터 <span class="katex-eq" data-katex-display="false">\vec A</span>를 검정색 화살표로 나타내었습니다.
[그림 1] (1)식에 주어진 벡터 A⃗\vec A를 검정색 화살표로 나타내었습니다.

1-2. 단위벡터

(1)식에 주어진 벡터 A⃗\vec A는 크기 ∣A⃗∣| \vec A|와 방향 정보를 갖는 단위벡터 A^\hat A가 결합된 형태로도 표기할 수 있어요. 아래 (2)식 처럼요.

A⃗=∣A⃗∣A^(2)\tag{2} \vec A = |\vec A| \hat A

그렇다면 (1)식에 주어진 벡터의 형식을 (2)식처럼 어떻게 바꿀 수 있을까요? 우선 벡터의 크기 ∣A∣|A|부터 구해봐요.

벡터의 크기는 각 성분의 크기값을 제곱하여 합한 후 제곱근을 구하면 됩니다. 아래 (3)식과 같이 숫자 7.1 이 (1)식에서 주어진 벡터 A⃗\vec A의 크기입니다.

∣A⃗∣=Ax2+Ay2+Az2=3.02+4.02+5.02=7.1(3)\tag{3} \begin{align} |\vec A| &= \sqrt{A_x^2 + A_y^2 + A_z^2}\\[10pt] &=\sqrt{3.0^2 + 4.0^2 + 5.0^2}\\[10pt] &=7.1 \end{align}

이번에는 단위벡터 A^\hat A를 구해보도록 하겠습니다. 이를 구하기 위해서는 (2)식을 아래 (4)식과 같이 바꿀 수 있을거에요.

A^=A⃗∣A⃗∣(4)\tag{4} \hat A = {{\vec A}\over{|\vec A|}}

이 식에서 A⃗\vec A는 (1)식으로 이미 주어져 있고, ∣A⃗∣|\vec A|는 (3)식을 통해 이미 구했습니다. 그러므로 그 값들을 대입하면 A^\hat A를 구할 수 있게 됩니다.

A^=A⃗∣A⃗∣=Axx^+Ayy^+Azz^∣A⃗∣=Ax∣A⃗∣x^+Ay∣A⃗∣y^+Az∣A⃗∣z^=3.07.1x^+4.07.1y^+5.07.1z^=0.42x^+0.56y^+0.70z^(5)\tag{5} \begin{align} \hat A &= {{\vec A}\over{|\vec A|}}\\[10pt] &= {{A_x \hat x + A_y \hat y + A_z \hat z}\over{|\vec A|}}\\[10pt] &={A_x\over{|\vec A|}}\hat x + {A_y \over |\vec A|}\hat y + {A_z \over{|\vec A|}}\hat z\\[10pt] &={3.0\over7.1}\hat x + {4.0 \over 7.1}\hat y + {5.0 \over{7.1}}\hat z\\[10pt] &=0.42 \hat x + 0.56 \hat y + 0.70 \hat z \end{align}

이제 비로소 (1)식으로 주어진 벡터 표기를 (2)식과 같이 할 수 있게 되었습니다.

A⃗=∣A⃗∣A^=7.1(0.42x^+0.56y^+0.70z^)(6)\tag{6} \begin{align} \vec A &= |\vec A| \hat A\\[7pt] &=7.1(0.42 \hat x + 0.56 \hat y + 0.70 \hat z) \end{align}

(6)식에서 괄호안에 있는 단위벡터는 크기가 1.0이고 방향은 A⃗\vec A의 방향과 동일합니다. 그렇다면 정말 이 단위벡터의 크기가 1.0이 나올까요? 단위벡터의 크기를 구해 보겠습니다.

크기를 구하는 방법은 (3)식의 방식을 그대로 적용하면 되요.

∣A^∣=A^x2+A^y2+A^z2=0.422+0.562+0.702=1.0(7)\tag{7} \begin{align} |\hat A| &= \sqrt{\hat A_x^2 + \hat A_y^2 + \hat A_z^2}\\[7pt] &=\sqrt{0.42^2 + 0.56^2 + 0.70^2}\\[7pt] &=1.0 \end{align}

정말 단위벡터의 크기가 1.0이 됨을 알 수 있습니다.

[그림 2] 벡터 <span class="katex-eq" data-katex-display="false">\vec A</span>와 단위벡터 <span class="katex-eq" data-katex-display="false">\hat A</span>를 각각 검정색과 빨강색 화살표로 나타내었습니다. 두 벡터의 방향은 서로 같습니다. 벡터 <span class="katex-eq" data-katex-display="false">\vec A</span>의 크기 <span class="katex-eq" data-katex-display="false">|\vec A|</span>는 검정색 화살표의 길이를 의미하고, 단위벡터의 크기는 (7)식에서와 같이 1이 됩니다.
[그림 2] 벡터 A⃗\vec A와 단위벡터 A^\hat A를 각각 검정색과 빨강색 화살표로 나타내었습니다. 두 벡터의 방향은 서로 같습니다. 벡터 A⃗\vec A의 크기 ∣A⃗∣|\vec A|는 검정색 화살표의 길이를 의미하고, 단위벡터의 크기는 (7)식에서와 같이 1이 됩니다.

[그림 2]는 A⃗\vec A와 단위벡터 A^\hat A의 모습을 검정색과 빨강색 화살표로 나타낸 것입니다.

2. 방향코사인 (방향여현)

이제부터 이번 글의 주제인 방향코사인을 이야기 하겠습니다. 방향코사인은 때로 방향여현으로 불리기도 합니다.

2-1. 방향코사인 정의

방향코사인이란 단위벡터를 표기하는 또 다른 방법으로 이해하시면 좋습니다.

앞서 단위벡터에 대해 여러 이야기를 했는데요. 그 중에서 (5)식이 단위벡터를 구하는 내용이었습니다. 그 내용을 다시 쓰면 아래와 같습니다.

A^=A⃗∣A⃗∣=Axx^+Ayy^+Azz^∣A⃗∣=Ax∣A⃗∣x^+Ay∣A⃗∣y^+Az∣A⃗∣z^(8)\tag{8} \begin{align} \hat A &= {{\vec A}\over{|\vec A|}}\\[10pt] &= {{A_x \hat x + A_y \hat y + A_z \hat z}\over{|\vec A|}}\\[10pt] &={A_x\over{|\vec A|}}\hat x + {A_y \over |\vec A|}\hat y + {A_z \over{|\vec A|}}\hat z\\ \end{align}

즉 벡터를 벡터의 크기로 나누어 단위벡터를 구하는 거죠.

이 말은 (8)식의 세번째 줄과 같이 각 방향 성분의 크기를 벡터의 크기로 나누는 것과 같습니다. 예를 들어 벡터 A⃗\vec A의 xx방향 성분의 크기가 AxA_x인데요. 이 값을 벡터 A⃗\vec A의 크기 ∣A⃗∣|\vec A|로 나누는 겁니다. 동일한 방식으로 yy와 zz방향 모두 적용됩니다.

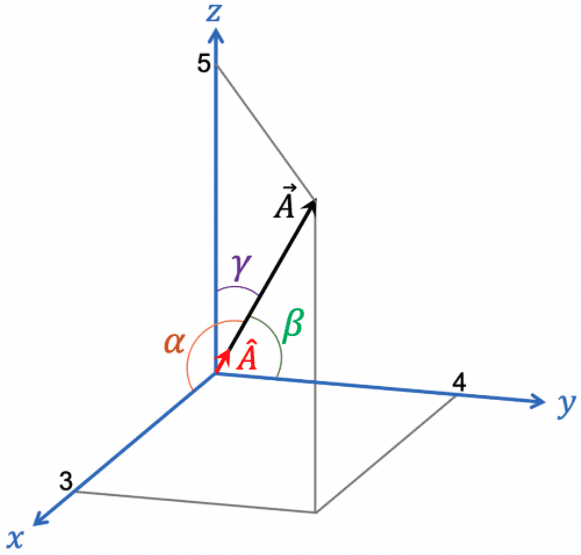
한편, 아래 [그림 3]은 벡터 A⃗\vec A와 양의 xx축, 양의 yy축, 양의 zz축 사이의 각도를 각각 α\alpha, β\beta, γ\gamma로 나타낸 그림인데요.

[그림 3] 방향코사인 정의. 벡터 <span class="katex-eq" data-katex-display="false">\vec A</span>와 양의 <span class="katex-eq" data-katex-display="false">x</span>축, 양의 <span class="katex-eq" data-katex-display="false">y</span>축, 양의 <span class="katex-eq" data-katex-display="false">z</span>축 사이의 각도를 각각 <span class="katex-eq" data-katex-display="false">\alpha</span>, <span class="katex-eq" data-katex-display="false">\beta</span>, <span class="katex-eq" data-katex-display="false">\gamma</span>라 할 때 이 각도에 코사인을 취한 것을 방향코사인이라 합니다.
[그림 3] 방향코사인 정의. 벡터 A⃗\vec A와 양의 xx축, 양의 yy축, 양의 zz축 사이의 각도를 각각 α\alpha, β\beta, γ\gamma라 할 때 이 각도에 코사인을 취한 것을 방향코사인이라 합니다.

이 그림을 보시면, 예를 들어 (8)식의 세번째 줄 세번째 항인 Az∣A⃗∣{{A_z}\over{|\vec A|}}를 다른 형식으로 표현한다면 어떻게 표현할 수 있을까요?

삼각함수에서 코사인이란 직각삼각형에서 빗변과 밑변의 길이의 비율을 뜻합니다. 즉 cos⁡θ=밑변빗변\cos \theta = {{밑변}\over{빗변}}이 되는 것이죠.

이 관계를 활용하면 벡터 A⃗\vec A의 크기인 ∣A⃗∣|\vec A|가 빗변의 길이로, zz축 방향의 크기인 AzA_z는 밑변의 길이로 대응시킨다면 다음과 같이 표현할 수 있습니다.

Az∣A⃗∣=cos⁡γ(9)\tag{9} \begin{align} {{A_z}\over{|\vec A|}} = \cos \gamma \end{align}

동일한 방식으로 xx축과 yy축을 모두 생각하면 다음 식도 성립합니다.

Ax∣A⃗∣=cos⁡α,   Ay∣A⃗∣=cos⁡β(10)\tag{10} \begin{align} {{A_x}\over{|\vec A|}} = \cos \alpha,~~~{{A_y}\over{|\vec A|}} = \cos \beta \end{align}

결국 어떤 벡터의 단위 벡터는 아래와 같이도 표현할 수 있습니다.

A^=A⃗∣A⃗∣=Axx^+Ayy^+Azz^∣A⃗∣=Ax∣A⃗∣x^+Ay∣A⃗∣y^+Az∣A⃗∣z^=(cos⁡α)x^+(cos⁡β)y^+(cos⁡γ)z^(11)\tag{11} \begin{align} \hat A &= {{\vec A}\over{|\vec A|}}\\[10pt] &= {{A_x \hat x + A_y \hat y + A_z \hat z}\over{|\vec A|}}\\[10pt] &={A_x\over{|\vec A|}}\hat x + {A_y \over |\vec A|}\hat y + {A_z \over{|\vec A|}}\hat z\\[10pt] &=(\cos \alpha) \hat x + (\cos \beta) \hat y + (\cos \gamma) \hat z \end{align}

이와 같이 단위 벡터의 각 방향 성분이 코사인으로 표기된다고 하여, 이를 방향코사인 또는 방향여현이라고 합니다.

2-2. 방향코사인 의미

단위벡터의 크기는 1이 되어야 합니다.

이를 알아보기 위해 우리는 이미 (5)식을 이용하여 단위벡터를 구한 후, (7)식을 이용하여 그 크기를 구했더니 정말 1이 나온다는 것을 확인했습니다.

따라서 (11)식에 방향코사인으로 표기된 단위벡터의 크기도 1이 되어야 합니다. 결국 다음의 관계가 성립한다는 의미가 되는 것이죠.

cos⁡2α+cos⁡2β+cos⁡2γ=1(12)\tag{12} \begin{align} \sqrt{\cos^2 \alpha + \cos^2 \beta + \cos^2 \gamma} =1\\ \end{align}

그러므로

cos⁡2α+cos⁡2β+cos⁡2γ=1(13)\tag{13} \begin{align} \cos^2 \alpha + \cos^2 \beta + \cos^2 \gamma =1 \end{align}

이 성립합니다.

결국 방향코사인 개념을 이용하면 어떤 벡터가 놓여진 각도를 구할 수 있어 편리하게 사용할 수 있습니다.

3. 방향코사인 구하는 문제 풀이

(예제1) B⃗=−4x^+2y^+3z^\vec B = -4 \hat x + 2 \hat y + 3 \hat z로 주어진 벡터가 있다. 이 벡터의 방향코사인 성분들을 구하여라.

(풀이) 수식으로는 (11)식을 이용하여 아래와 같이 정리할 수 있습니다.

B^=B⃗∣B⃗∣=Bxx^+Byy^+Bzz^∣B⃗∣=Bx∣B⃗∣x^+By∣B⃗∣y^+Bz∣B⃗∣z^=(cos⁡α)x^+(cos⁡β)y^+(cos⁡γ)z^(14)\tag{14} \begin{align} \hat B &= {{\vec B}\over{|\vec B|}}\\[10pt] &= {{B_x \hat x + B_y \hat y + B_z \hat z}\over{|\vec B|}}\\[10pt] &={B_x\over{|\vec B|}}\hat x + {B_y \over |\vec B|}\hat y + {B_z \over{|\vec B|}}\hat z\\[10pt] &=(\cos \alpha) \hat x + (\cos \beta) \hat y + (\cos \gamma) \hat z \end{align}

이 식을 이용하기 위해서는 우선 벡터의 크기 ∣B⃗∣|\vec B|를 구해야 합니다.

∣B^∣=B^x2+B^y2+B^z2=−42+22+32=29(15)\tag{15} \begin{align} |\hat B| &= \sqrt{\hat B_x^2 + \hat B_y^2 + \hat B_z^2}\\[10pt] &=\sqrt{-4^2 + 2^2 + 3^2}\\[10pt] &=\sqrt{29} \end{align}

그리고 다시 (14)식을 이용하여 방향코사인을 구하면 아래와 같습니다.

B^=B⃗∣B⃗∣=Bxx^+Byy^+Bzz^∣B⃗∣=Bx∣B⃗∣x^+By∣B⃗∣y^+Bz∣B⃗∣z^=(cos⁡α)x^+(cos⁡β)y^+(cos⁡γ)z^=−429x^+229y^+329z^(16)\tag{16} \begin{align} \hat B &= {{\vec B}\over{|\vec B|}}\\[10pt] &= {{B_x \hat x + B_y \hat y + B_z \hat z}\over{|\vec B|}}\\[10pt] &={B_x\over{|\vec B|}}\hat x + {B_y \over |\vec B|}\hat y + {B_z \over{|\vec B|}}\hat z\\[10pt] &=(\cos \alpha) \hat x + (\cos \beta) \hat y + (\cos \gamma) \hat z\\[10pt] &={{-4}\over{\sqrt{29}}} \hat x + {{2}\over{\sqrt{29}}} \hat y + {{3}\over{\sqrt{29}}}\hat z \end{align}

다시 한번 더 강조하면 방향코사인은 단위벡터를 표기하는 다른 표현일 뿐입니다.

(예제2) 어떤 벡터의 단위벡터가 C^=(1/2)x^+(1/2)y^+(1/2)z^\hat C = (1/2) \hat x + (1/\sqrt{2}) \hat y + (1/2) \hat z 로 주어졌다. 이 벡터가 xx축, yy축, zz축과 이루는 각도를 구하여라.

(풀이) 다음과 같이 정리할 수 있습니다.

C^=(cos⁡α)x^+(cos⁡β)y^+(cos⁡γ)z^=12x^+12y^+12z^(17)\tag{17} \begin{align} \hat C &= (\cos \alpha) \hat x + (\cos \beta) \hat y + (\cos \gamma) \hat z\\[10pt] &={{1}\over{2}} \hat x + {{1}\over{\sqrt{2}}} \hat y + {{1}\over{2}}\hat z \end{align}

그러므로 α, β, γ\alpha,~\beta, ~\gamma 각각의 각도는 60∘60^{\circ}, 45∘45^{\circ}, 60∘60^{\circ}가 됩니다.

흥미롭고 도움이 되는 글이었나요? 리뷰를 부탁드립니다.
[Total: 18 Average: 4.8]

Related posts.

단위 변환 – 환산 인자만 알면 단위의 변환은 아주 쉬워 SEM 구조 – (2) 주사전자현미경의 전체적인 구조와 구성 주사 전자 현미경에서 ‘주사’란 무엇인가? 평균 – 산술, 기하, 조화 평균의 개념과 실생활 활용 차트 또는 그래프 만들때의 필수 구성 요소 고도에 따른 중력 및 중력가속도 변화 극좌표계 (polar coordinate system) 시간 지연 : 특수상대성 이론

4 thoughts on “방향코사인 정의와 의미”

Leave a Comment