Last Updated on 2024-09-29 by BallPen
정상파가 수학적으로 어떻게 표현되는지 알아보고 그 파동의 모양을 관찰해 봐요.
정상파(standing wave)란 서로 반대방향으로 진행하는 파동이 중첩되어 마치 정지한 것처럼 보이는 파동을 말합니다.
여기서 정지해 보인다는 것은 파동이 위 아래로 진동하지만 옆으로 이동하지 않고 멈추어 있는 것처럼 보이기 때문이에요.
정상파 식은 다음과 같이 표현됩니다.
\tag{D1}
y = 2 A \sin (kx) \cos (wt)여기서 y는 정상파의 수직축 변위이고, A는 서로 반대방향으로 진행하는 파동의 진폭입니다. 또한 k는 파수이고, \omega는 각진동수에요.
이 글에서는 위 (D1)식이 어떻게 유도되었는지, 그리고 정상파의 파동 모양을 동영상으로 관찰해 봐요.
아래는 이번 글의 목차입니다.
Contents
정상파를 구현하기 위해 매스매티카를 사용했습니다. 매스매티카 코드는 아래 링크에서 다운받을 수 있어요.
1. 진행파(traveling wave)
진행파는 시간에 따라 옆으로 이동해 가는 파동을 말해요.
시간 t에 따라 +x 방향으로 이동하는 진행파는 다음과 같이 표기됩니다.
\tag{1-1}
y_1 = A \sin (kx - \omega t)여기서 A는 파동의 진폭이고, k는 파수(wave number)로 아래 (1-2)식처럼 파장 \lambda의 역수에 비례합니다. 그리고 \omega는 각진동수를 뜻해요.
\tag{1-2}
k = {{2 \pi}\over{\lambda}}그런데 (1-1)식의 \sin을 \cos으로 바꾸어도 되지 않을 까 생각할 수 있는데요. 그렇지 않습니다.
그 이유는 양끝이 고정된 줄에서의 정상파는 양 끝이 파동의 배가 절대로 될 수 없어요. 즉 양끝은 파동의 마디만 가능하므로 이를 충족하는 것은 \sin함수에요.
앞서 말씀드렸듯이 (1-1)식은 +x방향으로 이동하는 파동이고요. 만일 -x방향으로 이동하는 진행파를 표현하고 싶다면 다음과 같이 \omega t 앞의 부호만 +로 바꾸면 됩니다.
\tag{1-3}
y_2 = A \sin (kx + \omega t)2. 정상파 관계식
정상파를 표현하는 관계식을 유도해 보겠습니다. 먼저 정상파의 생성 조건을 이해해야 해요.
2-1. 정상파 생성 조건
정상파가 만들어지기 위해서는 진폭 A, 파수 k, 각진동수 \omega가 동일한 두 파동이 서로 마주 보며 반대방향으로 진행하며 중첩되어야 해요.
즉 (1-1)식과 (1-3)식의 두 진행파가 중첩되면 정상파가 생성되는 거에요.
2-2. 정상파 관계식 유도
정상파는 서로 마주보며 반대방향으로 진행하는 두 파동의 중첩에 대한 식을 만들고 정리하면 얻을 수 있어요.
(1-1)과 (1-3)식의 두 파동이 중첩되면 y = y_1 + y_2가 성립합니다. 그리고 이를 정리해 볼게요.
\tag{2-1}
\begin{align}
y &= y _1 + y_2\\
&=A \sin (kx - \omega t) + A \sin(kx+\omega t)\\
&=A(\sin kx \cos \omega t - {\cancel {\cos kx \sin \omega t}} + \sin kx \cos \omega t {\cancel {- \cos kx \sin \omega t)}}\\
&=2A \sin kx \cos \omega t
\end{align}윗 식의 결과만을 다시 쓰면 아래와 같아요. 이것이 정상파 관계식이에요.
\tag{2-2}
y = 2A \sin (kx) \cos (\omega t)식을 보면 2A \sin (kx)는 공간 상에 만들어진 정지된 사인 파동인데, 이 상태에 +1에서 -1까지 시간에 의존하여 부호가 반복적으로 변하는 \cos (\omega t)가 곱해졌음을 알 수 있어요.
그러므로 (2-2)식은 2A \sin (kx)의 파동이 주기적으로 부호가 바뀌어 파동의 배는 위 아래로 진동하고 마디는 멈춰있는 정상파를 만들게 됩니다.
3. 정상파 진동 모습
그럼 이제부터 양끝이 고정된 줄에서의 정상파를 동영상으로 보여드리겠습니다.
3-1. 길이가 L인 줄에서의 정상파
줄의 길이를 L이라 했을 때 정상파가 형성될 파장 \lambda는 다음의 관계를 만족해야 해요.
\tag{3-1}
L = {1 \over 2} \lambda,~~ L = {2 \over 2} \lambda,~~L={3 \over 2}\lambda,~~ \cdots위 식을 양자수 n을 도입하여 정리해 봐요.
\tag{3-2}
L = {n \over 2}\lambda~~~~~~~~~~(n=1, 2, 3,\cdots)그리고 윗 식의 \lambda를 (1-2)식의 파수 k에 대입 후 정리하면 정상파 관계식 (2-2)식은 다음과 같습니다.
\tag{3-3}
y = 2A \sin \Big({{n \pi}\over{L}}x \Big) \cos (\omega t)3-2. 정상파
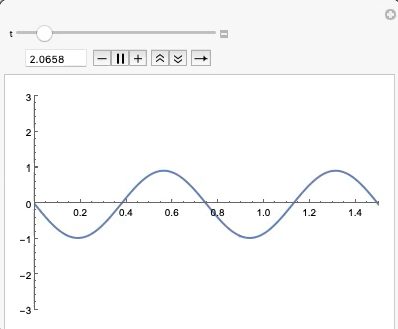
아래 동영상들은 (3-3)식에서 A=2, L=1.5, \omega=1인 경우입니다.
그리고 아래 동영상은 n=1인 제1조화모드 입니다.
그리고 아래 동영상은 n=2인 제2조화모드 입니다.
그리고 아래 동영상은 n=3인 제3조화모드 입니다.
그리고 아래 동영상은 n=4인 제4조화모드 입니다.