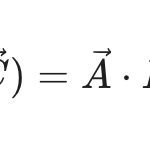조명 – 단색광, 다색광, 복사선속, 광선속, 광도, 조도, 휘도의 완벽 정리

Last Updated on 2024-03-04 by BallPen

단색광, 조도, 휘도, 광도 등 조명과 관련된 다양한 용어가 존재합니다. 이 용어들에 대한 정의와 개념을 정리했습니다.

조명 학문 분야에는 다양한 용어가 존재합니다. 단색광, 다색광, 복사측정, 측광, 광도, 조도, 휘도 등 얼핏 단어만 들어서는 그 뜻을 헤아리기가 쉽지 않습니다.

이에 따라 각각의 용어에 대한 정의와 개념을 명확하게 정리하였습니다.

다만 영어 용어에 대응하는 한글 물리 용어가 확실하게 정의되지 않은 것이 많습니다.

독자의 이해를 돕기 위해 한글 용어에 영어를 병기하였습니다. 목차는 다음과 같습니다.

1. 단색광과 다색광 (Monochromatic light and Polychromatic light)

단색광(Monochromatic light)이란 하나의 단일 파장을 갖는 빛을 말합니다. 대표적으로 레이저는 단색광을 방출하는 기기입니다.

이에 비해 다색광(polychromatic light)은 파장 분포를 갖는 빛을 말하며, 대표적으로 햇빛이 있습니다.

2. 복사측정과 측광 (Radiometry and Photometry)

복사측정(Radiometry)이란 전자기파의 일정 영역에 대한 특성들을 측정하는 과학의 한 분야입니다. 일반적으로 가시광선을 포함한 자외선에서 적외선까지의 범위를 다룹니다.

이와 달리 측광(photometry)이란 사람 눈이 인식할 수 있는 가시광선 영역의 특성들에 대해 눈의 민감도를 반영하여 측정하는 과학의 한 분야입니다. 사람이 갖는 빛의 민감성에 대한 통계적 모델을 기반으로 만들어진 분야입니다.

3. 조명 분야에서의 일률 (Flux)

조명 분야에서도 일률 또는 출력(power)의 개념이 사용되는데 그것이 복사선속(radiant flux)과 광선속(Luminous flux)입니다. 복사선속은 적외선에서 자외선까지 광원으로부터 방출되는 출력의 총합입니다. 이에 비해 광선속은 측정된 복사선속을 사람의 빛에 대한 민감도로 보정한 것입니다.

3-1. 복사선속 (Radiant flux)

복사선속(Radiant flux)이란 단위시간 t당 광원에서 방출되는 광자들의 총 에너지 U로서 출력의 단위인 W (와트)가 사용됩니다. 기계가 측정하는 값으로서 인간의 빛에 대한 민감도가 반영되어 있지 않습니다. 즉 사람 눈에 보이지 않는 영역도 다루어 집니다.

어느 단일 파장에서의 복사선속은 아래와 같이 정의됩니다.

\tag{1}
\begin{align}
\Phi_e =  {{\partial U}\over{\partial t}} ~~~~ [ \mathrm{J/s, ~W} ]
\end{align}

그러나 실제의 경우 빛은 넓은 범위의 파장에 걸쳐 방출되므로 적외선부터 자외선까지의 총 복사선속은 다음과 같이 구할 수 있습니다.

\tag{2}
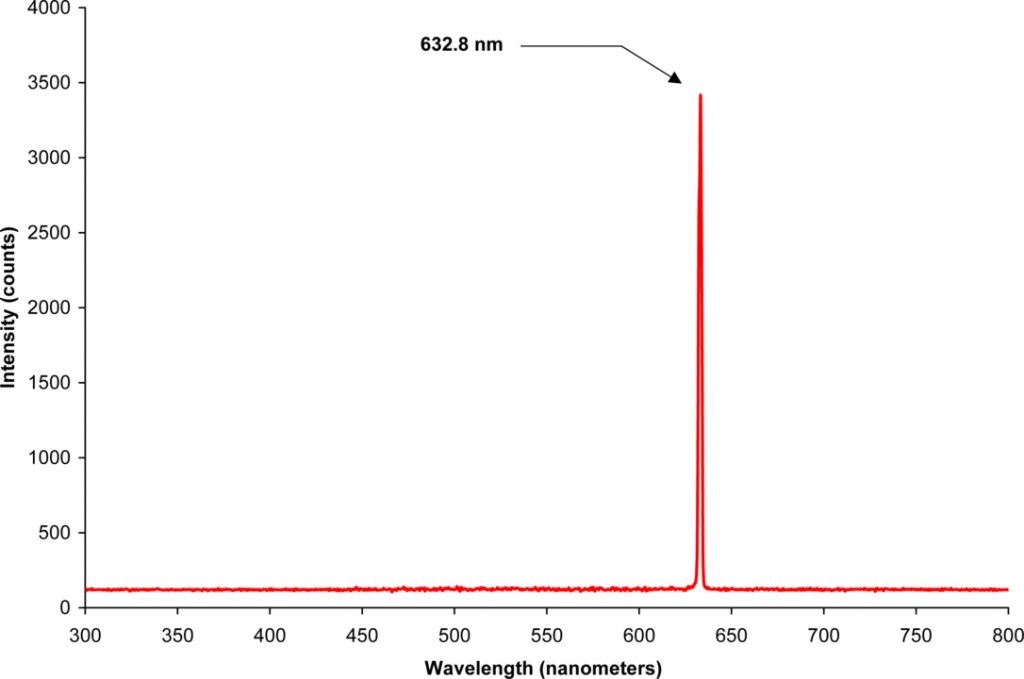
P = \int_{적외선파장값}^{자외선파장값} {\partial \Phi_e ( \lambda )\over{ \partial \lambda }}~d \lambda

여기서 적분기호 안에 있는 \partial \Phi_e( \lambda )\over{\partial \lambda }는 보통 \Phi_{e, \lambda}(\lambda) 의 기호로 표기됩니다. 이 값은 spectral flux라고 하며 단위 파장당 복사선속을 뜻합니다. 단위는 보통 \mathrm{W/nm}를 사용합니다. Spectral flux는 아래 그림에 있는 적분구(integrating sphere)를 이용해 측정합니다.

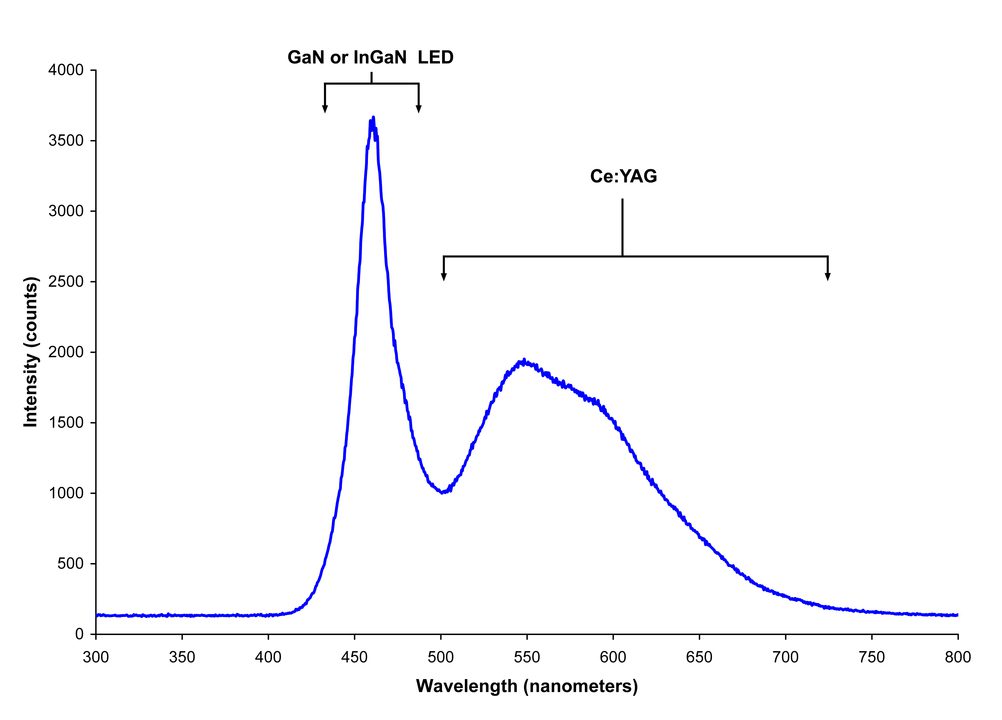
위에 있는 그래프는 적분구로 광원의 모든 방향에서 방출되는 빛에 대한 spectral flux \Phi_{e, \lambda}(\lambda) 를 측정한 예시입니다. x축이 파장이고 y축이 spectral flux입니다.

(2)식에 주어진 총 복사선속 \(P\)을 구하기 위해서는 위 예시 그래프에서 보여지는 곡선의 아래쪽 면적을 구하면 됩니다. 컴퓨터를 이용해 구했더니 626.657 W가 얻어졌습니다.

여기서 중요한 것은 복사선속을 구하기 위해 사용되는 spectral flux는 기계로 측정한 양이라는 것입니다. 복사선속이나 spectral flux는 물리학을 하는 사람들에게는 과학적으로 중요할 수 있습니다.

그러나 사람 눈의 관점에서 가시광선 영역의 빛만을 다루는 조명 분야에서는 복사선속을 그대로 사용하기가 적당하지 않습니다.

이에 따라 사람 눈의 빛의 민감도를 반영한 광선속이 도입되었습니다.

3-2. 광선속 (Luminous flux)

광선속(Luminous flux)이란 복사선속을 사람 눈의 빛에 대한 민감도로 보정한 선속입니다. 단위는 lm (루멘)을 사용합니다. 광선속은 적분구로 측정한 복사선속을 사람 눈의 민감 효율 곡선(비시감도, luminous efficiency)과 곱하고 가시광선 파장 영역에 대해 적분하여 구합니다. 식으로 표현하면 다음과 같습니다.

\tag{3}
\Phi_V = K_m \int_{380}^{780}  \Big( \Phi_{e, \lambda} (\lambda) \times  \bar{y} (\lambda) \Big) d\lambda

(3)식에서 K_m은 683 lm/W로 주어지는 상수로서 SI 단위인 광도를 정의할 때 도입된 수치입니다. 복사선속 1 W당 광선속 몇 lm에 해당하는지를 나타내는 환산인자라고 생각하시면 쉽습니다.

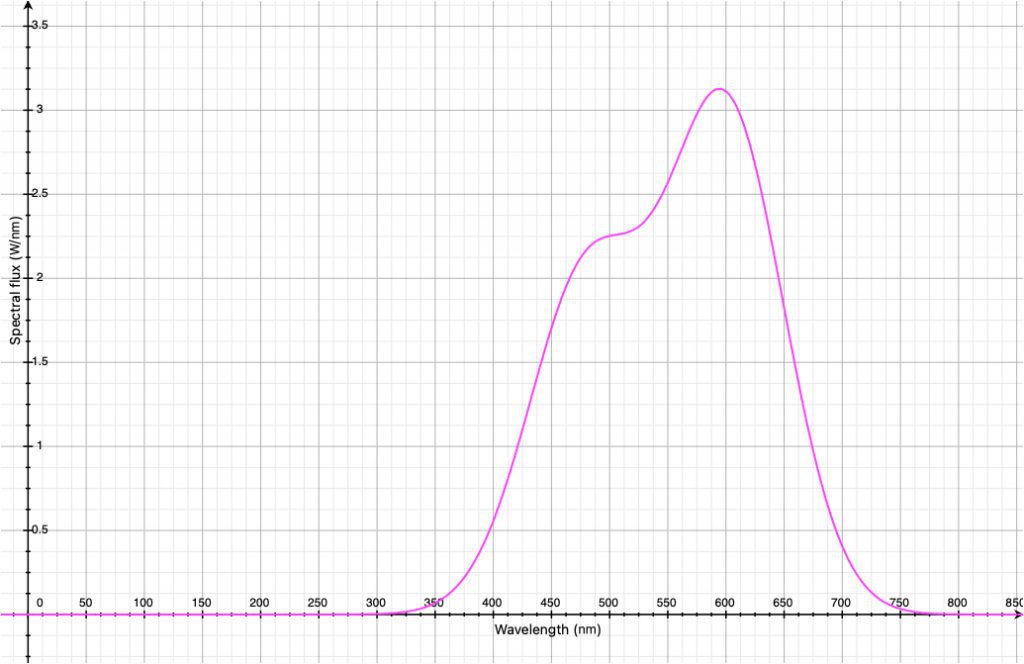
그리고 \Phi_{e, \lambda}(\lambda) 는 바로 위의 예시자료1에서 제시된 그래프에 대응합니다.

\bar{y} ( \lambda ) 는 빛의 파장별 사람 눈의 민감 효율을 의미합니다. 바로 아래 쪽 그래프에 제시하였습니다. 이 그래프에 따르면 사람은 555 nm(green)의 빛에 대해 가장 민감하고 380 nm(보라색)에서 780 nm(붉은색)의 빛은 효율이 떨어집니다.

예를 들어 470 nm와 555 nm에서 1 mW의 동일한 복사선속을 갖는 빛이 방출된다고 했을 때 사람은 555 nm의 빛을 470 nm보다 약 10배 밝다고 느끼게 됩니다.

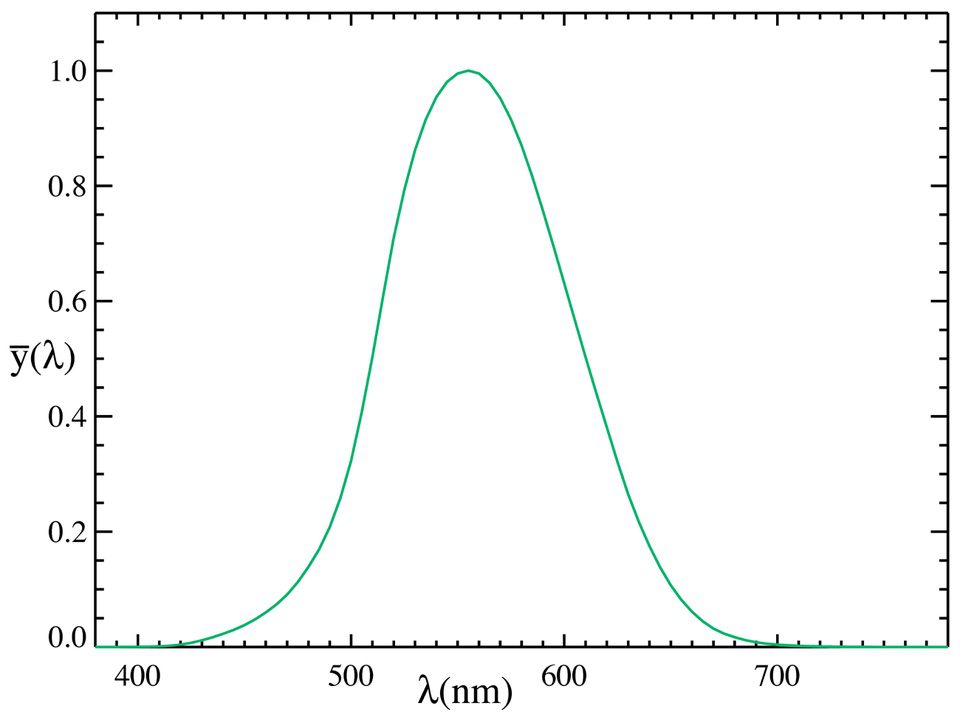
아래 그래프는 위 그래프에서 제시된 사람 눈의 민감 효율 \bar{y} ( \lambda )을 계산을 위해 가우시안 곡선으로 개략적으로 나타낸 예시자료입니다.

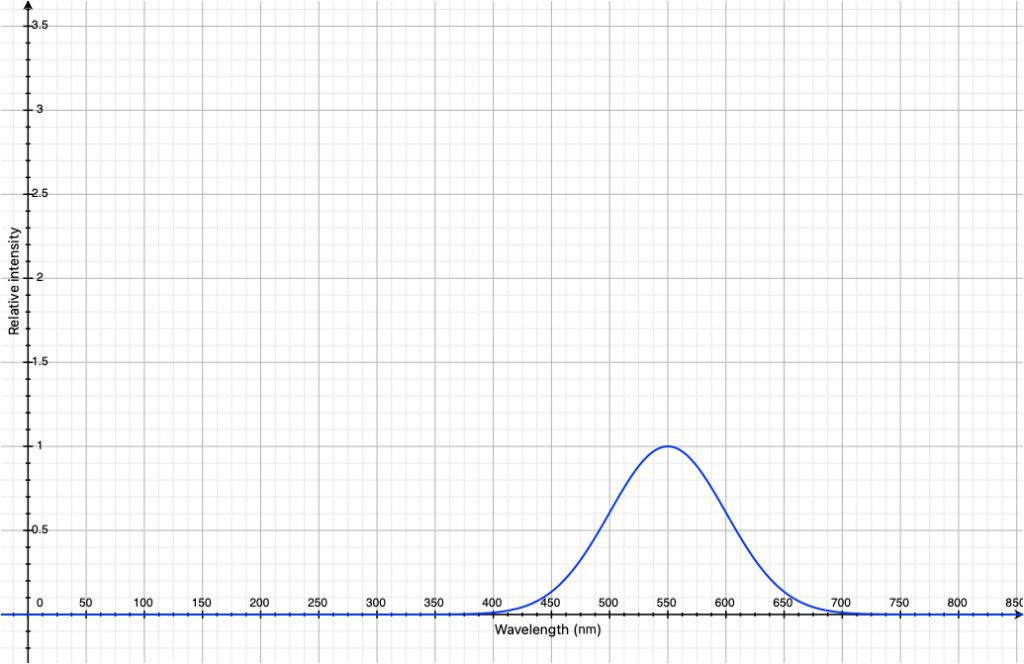
아래 그래프는 \Phi_{e, \lambda}(\lambda) 와 \bar{y} (\lambda) 의 예시자료1과 2를 곱한 후의 모습입니다. \Phi_{e, \lambda}(\lambda) (예시자료1)가 300 nm~800 nm로 넓더라도 \bar{y} (\lambda) (예시자료2)와의 곱에 의해 사람 눈이 보이는 가시광선 영역만의 spectral flux가 구해지게 됩니다.

(3)식에서 주어진 적분은 바로 위 그래프에서 제시된 곡선의 안쪽 면적을 뜻합니다. 컴퓨터를 이용해 그 면적을 구해보았을 때 315.6435 W가 도출되었습니다.

결국 (3)식으로 최종 광선속 \Phi_V 을 구하면 215,584 lm이 나옵니다.

\tag{4}
\begin{align}
\Phi_V &= K_m \times 315.6435 ~\mathrm{W} \\
&= 683 ~{{\mathrm{lm}}\over{\mathrm{W}}} \times 315.6435 ~\mathrm{W} \\
&= 215,584 ~\mathrm{lm}
\end{align}

4. 조명 광원에서 특정 방향의 밝기를 결정하는 광도 (luminous intensity)

앞서 설명한 광선속은 모든 방향으로 퍼져나가는 빛의 복사선속을 사람 눈의 민감효율로 보정한 양이라고 말하였습니다. 그러므로 복사선속이나 광선속은 광원마다 일정한 값을 갖게 됩니다.

그런데 광원의 형태에 따라 빛이 사방으로 고르게 퍼져나가는 광원이 있고 특정한 방향으로 주로 퍼져나가는 광원이 있을 수 있습니다.

예를 들어 아래 사진의 백열전구는 소켓부분을 제외한 사방으로 빛을 방출합니다. 만일 소켓이 없는 이상적인 백열전구가 있다면 모든 방향으로 고르게 빛이 방출될 것입니다.

이에 비해 아래 사진의 가로등은 지면쪽을 향해 주로 빛을 방출하도록 설계되어 있습니다.

결국 동일한 광선속을 갖는 광원일지라도 광원의 형태에 따라 빛을 방출하는 지향성이 서로 다를 수 있습니다. 따라서 특정 방향으로 방출되는 광선속의 양을 정의할 필요가 있어요.

이를 적용하면 이상적인 백열전구의 경우 방향당 광선속은 모두 동일하게 나올것입니다. 그러나 가로등의 경우에는 지면쪽 방향은 광선속이 크게 나오고 하늘쪽 방향은 광선속이 작게 나오겠죠.

이러한 빛의 지향성 개념을 광도(luminous intensity)라고 하며, 광원을 중심으로 단위 입체각당 광선속으로 정의합니다.

이를 구체적으로 이해하기 위해서는 아래 그림을 보아주세요. 그리고 광원을 중심으로 하는 특정한 입체각 \Omega을 생각해 보세요. 그러면 그 입체각 안으로 광원에서 방출된 광선속이 지나가게 될 것입니다. 그림에서와 같이 입체각이 결정되면 광원으로부터의 거리에 따른 평면의 면적과 무관하게 모두 동일한 광선의 수(화살의 갯수)가 지나가게 되죠.

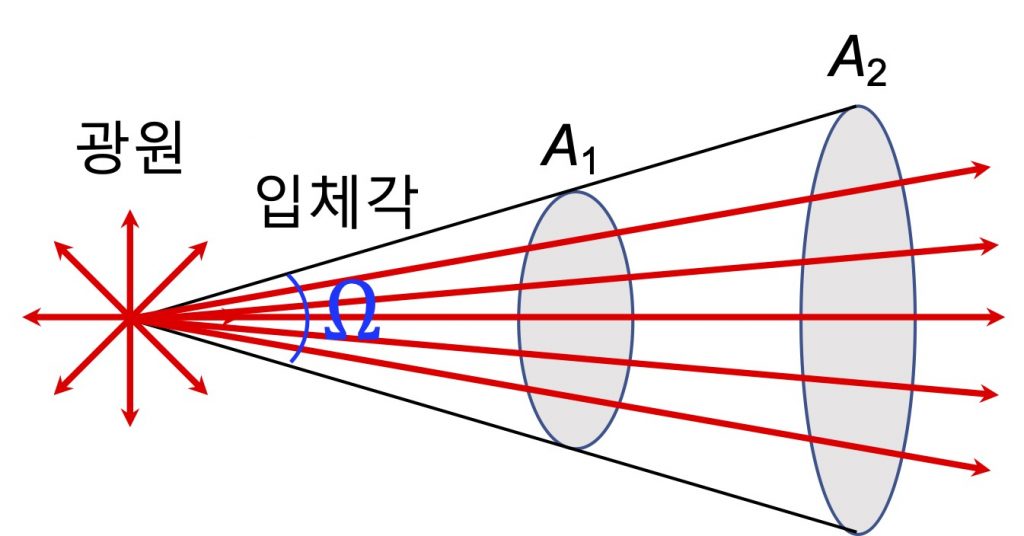
이러한 개념을 이용해 광도 I_V는 다음과 같이 정의되며, 단위는 lm/sr 또는 cd(칸델라)가 됩니다.

\tag{5}
I_V = {{광선속}\over{입체각}} = {{\Phi_V}\over{\Omega}}~~~[\mathrm{lm/sr,~cd}]

<예제 풀이>

(예제) 예를 들어 2.0 sr에서 광선속이 34,328 lm이 나왔다면 그 광원의 광도는 얼마인가?

(풀이) 수식 (5)에 적용하여 풀이하면 됩니다.

\tag{6}
I_V = {{34,328 ~\mathrm{lm}}\over{2.0~{\mathrm{sr}}}} = 17,164 ~\mathrm{cd}

광도는 17,164 lm/sr 또는 17,164 cd가 됩니다.

여기서 중요한 것은 광도는 복사선속, 광선속과 같이 광원으로부터의 거리에 따라 변하지 않는다는 것입니다. 복사선속, 광선속, 방향별 광도는 광원을 설계한 사람이 기본적으로 결정하는 수치들입니다.

5. 조명 광원으로부터의 거리에 따른 조도 (illuminance)

일반적으로 사람들은 가게에서 판매하는 조명을 구매하여 사용합니다. 그 조명들은 기본적으로 복사선속, 광선속, 방향별 광도가 이미 결정되어 있습니다. 여러분들은 단지 그 조명들을 사용할 뿐입니다.

그런데 이때 또 하나 생각해야할 것이 있습니다. 비로 광원으로부터 거리에 따른 빛의 밝기 변화입니다.

여러분들이 가로등 밑에서 책을 보고 있다고 생각해 보세요. 가로등의 복사선속, 광선속, 지면쪽 광도는 이미 가로등을 만드는 회사에서 일정한 값을 갖도록 제작되어 있습니다.

그런데도 가로등으로부터 거리가 멀어질 수록 밝기가 어두워져 책을 보기가 어려운 이유는 무엇일까요?

바로 이것이 조도(illuminance)와 관련된 내용입니다. 조도를 이해하기 위해서는 아래 그림을 보아주세요.

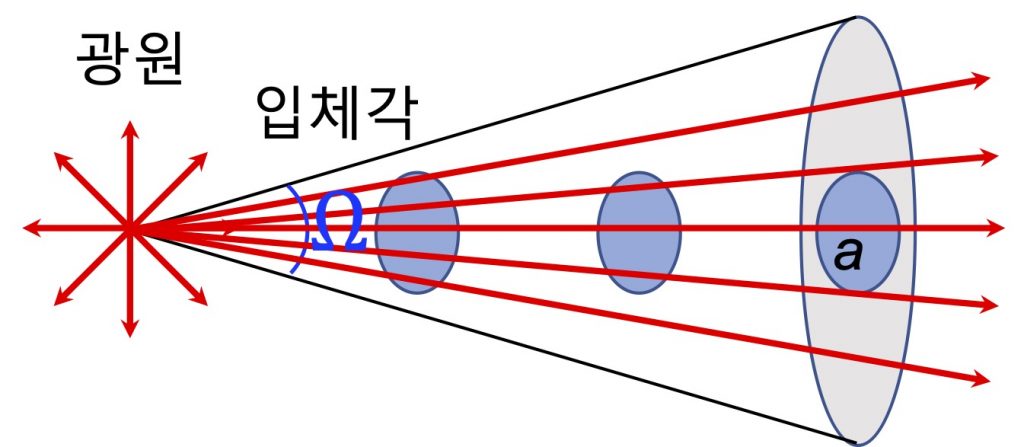
앞에서 말한 것처럼 광도는 단위입체각을 통과하는 광선속의 크기입니다. 그러므로 광원으로부터의 거리에 무관하게 동일한 값을 같게 되는데요. 조도는 그렇지 않습니다. 바로 거리에 따라 달라지는 양입니다.

위 그림에는 배경색이 있는 세 개의 원이 있습니다. 그 원의 면적은 모두 동일해요. 예를들어 그 원의 면적을 여러분들이 보고 있는 책의 면적이라고 생각하셔도 좋습니다.

그런데 그 책의 면적을 통과하는 입사 광선속(incident )의 갯수를 보면 광원에서 가까울때에는 5개의 광선속이 지나가고, 조금 멀리 있을 때는 3개의 광선속이 지나갑니다. 아주멀리 있을 때는 단지 1개의 광선속만 지나가는 군요.

바로 이것이 뜻하는 것은 여러분들이 보고 있는 책에 비추어지는 빛의 밝기가 광원으로부터의 거리가 멀어질수록 점점 어두워진다는 것을 뜻합니다.

이러한 개념을 이용해 조도 E_V는 다음과 같이 정의되며, 단위는 lm/m² 또는 lx(럭스)가 됩니다.

\tag{7}
\begin{align}
E_V &= {{광선속}\over{단위면적}} \\[10pt]
&= {{\Phi_V}\over{a}} ~~~[\mathrm{lm/m^2},~ \mathrm{l_x}]
\end{align}

<예제 풀이>

(예제) 예를 들어 사방으로 균일한 광도를 갖는 광원이 있다고 하겠습니다. 이 광원으로부터 1.5 m 떨어진 아래에 바닥이 구의 일부(shperical cap)로서 오목하게 만들어진 거대한 후라이펜이 있다고 상상해 보세요. 이 후라이펜의 표면적이 6.0 m²인 경우에 후라이펜을 비추는 빛의 조도는 얼마일까요? 단 광원에서 방출되는 총 광선속 \Phi_V는 215,584 lm입니다.

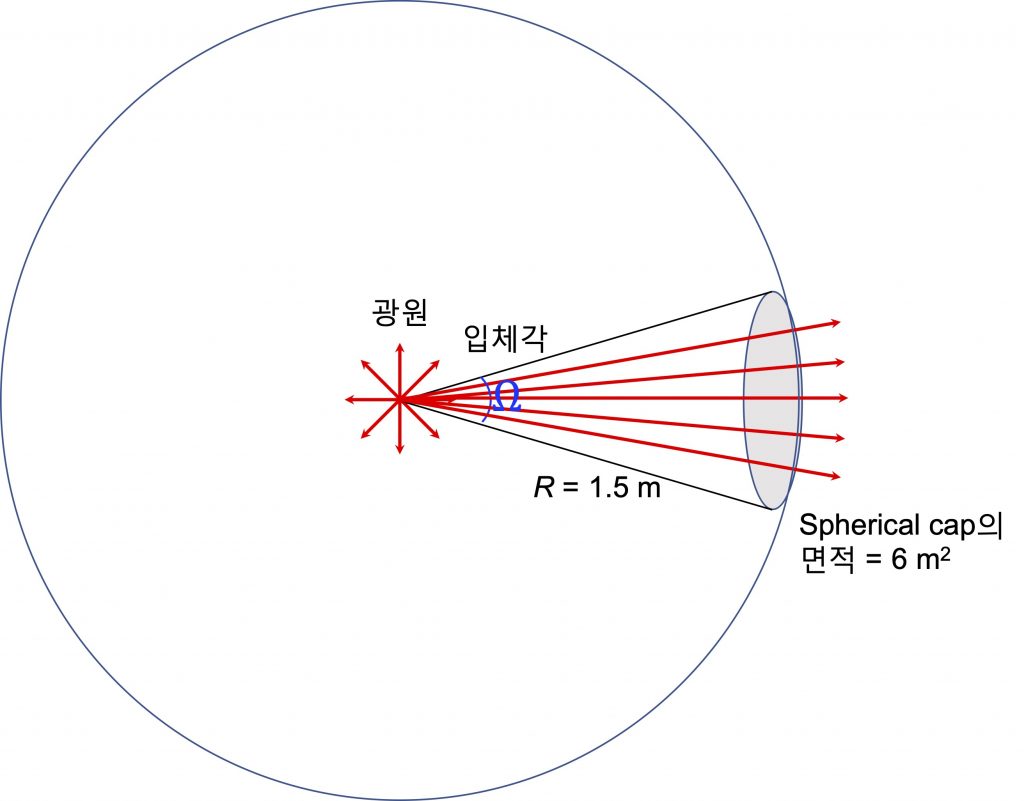
(풀이) 반지름이 R = 1.5 m인 구의 전체 표면적 4 \pi R^2 = 28.3 m²을 통해 215,584 lm의 광선속이 통과합니다. 그러므로 6.0 \mathrm{m^2}을 통과하는 입사 광선속을 비례식으로 구하면 약 45,706.9 lm이 나옵니다.

\tag{8}
28.3 ~\mathrm{m^2} : 215,584~\mathrm{lm} = 6.0 ~\mathrm{m^2} : x~\mathrm{lm}

\tag{9}
\begin{align}
x~{\mathrm{lm}} &= {{215,584~{\mathrm{lm} \times {6.0~\mathrm{m^2}}}}\over{28.3~\mathrm{m^2}}} \\
&=45706.9~\mathrm{lm}
\end{align}

그러므로 (7)식을 이용해 조도를 구하면 7617.8 lx가 나옵니다.

\tag{10}
E_V = {{{45,706.9~ \mathrm{lm}}}\over{6.0~\mathrm{m^2}}} \approx 7617.8 ~\mathrm{lx}

그렇다면 이번에는 광원으로부터 3 m가 떨어져 있고 나머지 조건은 모두 동일하면 조도는 얼마가 나올까요? 위에서와 같은 방식으로 그대로 풀면 됩니다. 단 R=3 m만 바꾸어주시면 되는데요.

풀어보시면 약 1907.8 lx가 나옵니다.

계산 결과와 같이 광원으로부터의 거리가 커질수록 조도는 점점 작아지게 됩니다.

조도 값은 조도계를 이용해 측정합니다.

6. 조명 분야에서 최근 많이 활용하는 휘도 (luminance)

과거에는 인간이 만들어낸 불빛이라고는 장작불, 촛불, 백열전구 등이 전부였습니다. 이러한 광원의 특징은 사방으로 불빛이 퍼져나가고 조금만 멀리 떨어져도 하나의 점 광원으로 간주할 수 있었습니다.

그러나 시대가 변하면서 면이 광원역할을 하는 경우가 있습니다.

대표적으로 텔레비전, 휴대폰 화면, 조명이 내장된 광고판넬, 벽면을 이용한 간접 조명, 면에서 반사된 빛 등 점이 아닌 면이 조명의 역할을 하게 됩니다.

따라서 점광원이 아닌 면광원에서 방출된 빛의 양에 대한 평가 개념으로 휘도 (luminance)가 도입되었습니다.

휘도는 현대의 공간 인테리어나 조명 설계 등에 중요한 역할을 합니다.

예를 들어 가로등 높이는 보통 10 m 높이에 있습니다. 그러므로 가로등불이 켜지면 주변으로 빛을 방출하게 되는데요.

가로등이 일정한 높이에 고정되어 있으므로 가로등의 복사선속, 광선속, 광도, 조도 모두 일정한 값을 갖게 됩니다.

그런데 가로등 밑을 걸어가는 사람이 검은색 옷을 입었을때와 흰색 옷을 입었을 때 주변에서 사람을 인식하는 정도는 차이가 있습니다.

검은색 옷을 입은 사람보다 하얀색 옷을 입은 사람을 더 발견하기 쉬운데요.

그 이유는 똑같은 조도 상황에서 검은색 보다 하얀색이 빛을 더 반사하여 관찰자에게 더 많은 빛을 보내기 때문입니다. 이러한 차이가 바로 휘도입니다.

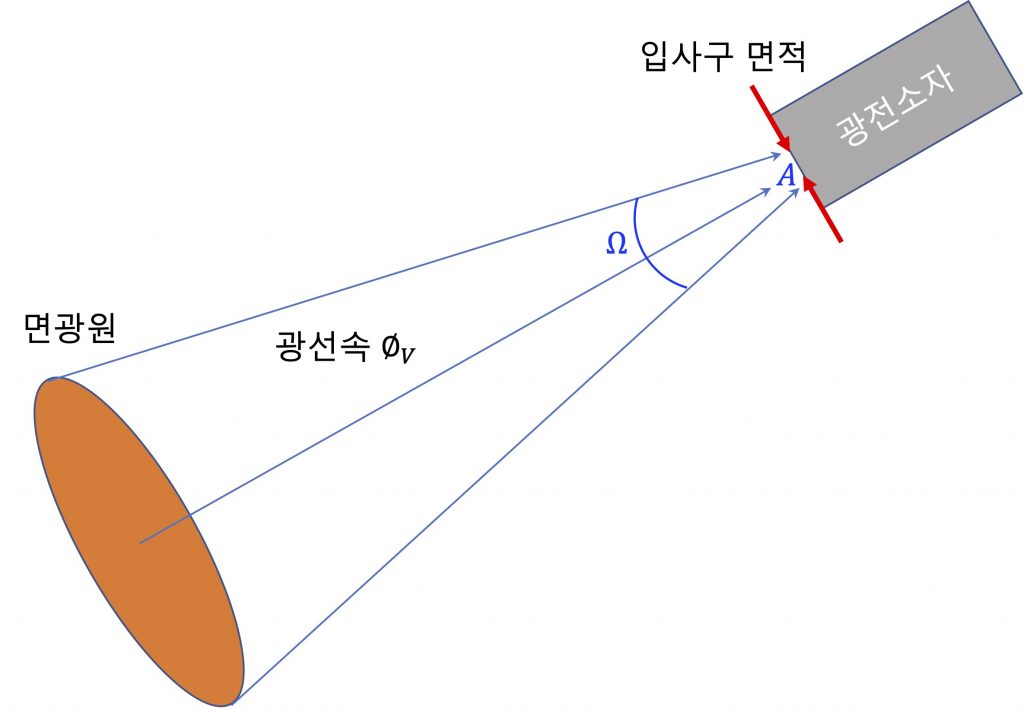
휘도는 면광원에서 방출된 빛 또는 반사된 빛을 위 그림과 같이 특정한 입체각 \Omega과 입사구 면적 A를 통해 휘도계의 광전소자 센서로 받아들여 측정됩니다. 그러면 아래의 식을 통해 휘도값을 계산합니다.

\tag{11}
\begin{align}
L_V &= {{광도}\over{단면적}} = {{광선속/입체각}\over{단면적}} \\[10pt]
&= {{d \Phi_V / d\Omega}\over{dA}} \\[10pt]
&= {{d \Phi_V}\over{d \Omega \cdot dA}}~~~[\mathrm{cd/m^2, ~lm/(sr \cdot m^2})]
\end{align}

휘도는 휘도계로 측정합니다.

7. 조명 관련 용어의 요약 정리

• 단색광이란 단일의 파장을 갖는 빛이고 다색광은 넓은 파장범위를 갖는 빛입니다.
• 복사측정이란 자외선에서 적외선까지의 빛의 특성을 측정하는 학문이며, 측광이란 복사측정을 비시감도로 보정하여 빛의 특성을 다루는 학문입니다.
• 복사선속이란 단위시간동안 광원에서 방출되는 에너지의 총량입니다.
• 광선속이란 복사선속을 비시감도로 보정한 선속입니다.
• 광도란 광원에서 단위 입체각당 방출되는 광선속의 양입니다.
• 조도란 광원으로부터 일정한 거리의 단위 단면적을 통과하는 광선속의 양입니다. 그러므로 광원으로부터의 거리가 멀어질수록 조도는 감소하게 됩니다.
• 휘도란 조도가 일정할 지라도 반사면의 성질에 따라 반사광의 강도가 달라질 수 있는데 이를 휘도라 합니다. 면광원에서도 휘도가 활용됩니다.

Related posts.

일률(power) 관성질량 vs 중력질량 – 진공에서 자유낙하하는 볼링공과 깃털의 운동 SEM 전자총 원리와 총을 갖고 싶던 어린 시절의 값비싼 추억 표준 오차 계산 예제 벡터의 방향 표기를 정확하게 하는 방법 내적의 분배법칙 등온 과정 (isothermal process) 전하 (electric charge)