Last Updated on 2024-03-03 by BallPen
측정 기술 분야에서 정확도와 정밀도는 구분해서 사용해야 합니다. 또한 측정 값의 정확도와 정밀도를 계산하여 숫자로 표기하는 방법도 알아봅니다.
측정 관련 용어로 가장 처음에 익히는 개념이 정확도(accuracy)와 정밀도(precision)입니다. 두 개념은 서로 비슷해서 일반인들은 많이 혼용해서 사용하는데요.
과학이나 공학을 하는 분들은 ‘속력과 속도‘처럼 이 두 개념을 무척 엄밀하게 구분합니다. 아울러 여기에서 설명드리는 정밀도는 유효 숫자 개념에서의 정밀도와는 다른 개념입니다.
이에 대한 내용을 소개합니다. 목차는 아래와 같습니다.
Contents
1. 양궁 경기에서 과녁에 꽂힌 화살의 분포
우리 나라의 양궁 위상은 전세계적으로 최상위입니다.
양궁은 활로 화살을 쏘아 과녁을 맞추는 스포츠인데요. 화살이 과녁의 정중앙을 맞추게 되면 양궁 선수의 기량에 감탄을 하게 됩니다.
(출처 : “Incheon_AsianGames_Archery_14” by KOREA.NET – Official page of the Republic of Korea is licensed under CC BY-SA 2.0)
아래 사진은 화살이 과녁을 맞춘 모습입니다. 과녁의 중앙에 화살이 꽂히는 경우도 있지만 중앙으로부터 상대적으로 먼곳에 화살이 꽂히기도 합니다.
이렇게 과녁의 중앙을 기준으로 화살이 꽂힌 분포를 보고 정확도와 정밀도에 대한 이야기를 시작할 수 있습니다.
(출처 : “Archery Lessons” by ProAdventure is licensed under CC BY 2.0)
2. 측정 기술 분야에서 정확도와 정밀도의 정의 및 차이
아래 그림은 과녁에 꽂힌 화살의 위치를 크게 4개로 구분하여 제시하고 있습니다.
A1(가로방향 A, 세로방향 1번) 그림은 전체적으로 화살이 과녁의 중앙으로부터 한쪽으로 몰려 있고 그 분포도 매우 넓습니다. 이에 비해 A2 그림은 화살이 중앙에서 한쪽으로 몰려있는 것은 동일하나 그 분포가 매우 좁다는 것을 볼 수 있습니다.
B1 그림은 대체적으로 화살이 과녁의 중앙 부분에 몰려 있으나 그 분포가 매우 넓습니다. 이에 비해 B2 그림은 화살이 과녁의 중앙에 몰려 있으며 그 분포도 매우 좁습니다.
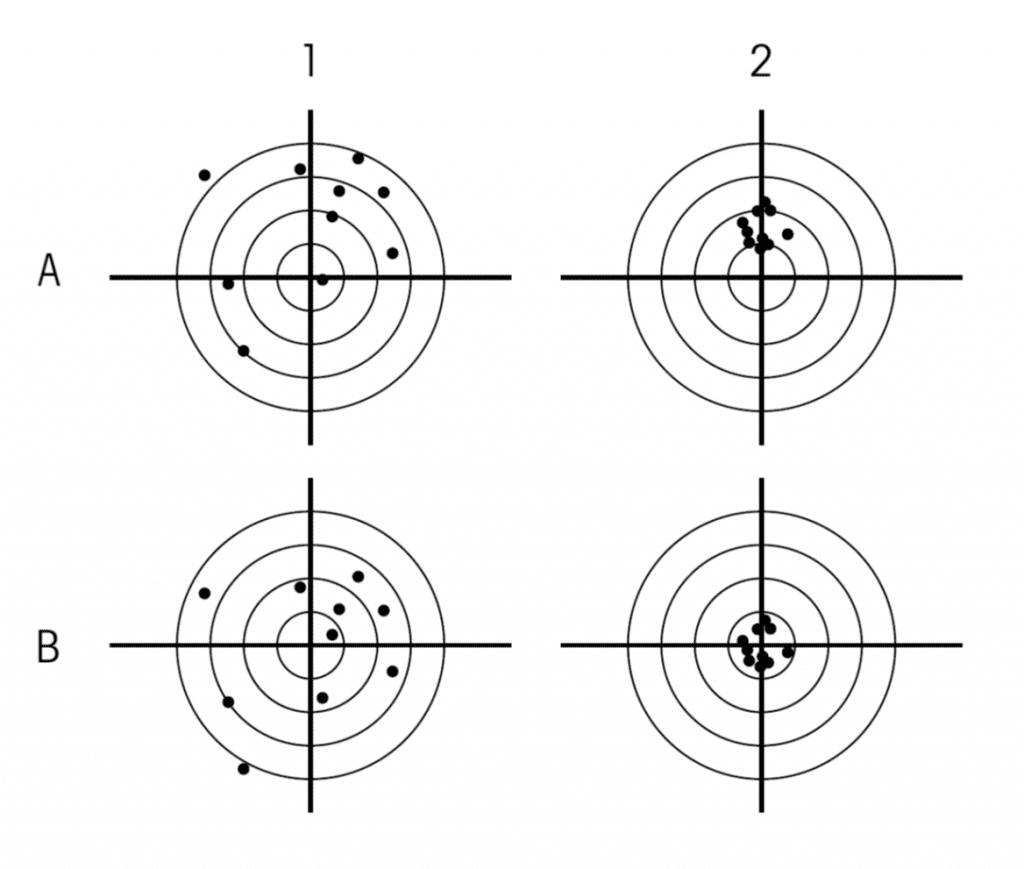
(출처 : By Sgiani – Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=88745978)
2-1. 정확도와 정밀도의 정의
오차론에서 정확도와 정밀도는 다음과 같이 정의합니다.
정확도 : 측정값들이 한쪽으로 몰리는 일이 적은 정도. 즉 계통오차가 적은 정도를 나타내는 개념
정밀도 : 측정값들의 퍼짐이 좁은 정도. 즉 우연 오차가 적은 정도를 나타내는 개념
2-2. 정확도와 정밀도의 차이
정확도와 정밀도에 대한 정의의 차이를 토대로, 화살의 정확도와 정밀도를 상대적으로 판단할 수 있어요.
A1 그림은 화살이 중앙으로부터 한쪽으로 몰려있어 정확도가 낮고 화살의 분포가 넓어 정밀도도 낮습니다. 이에 비해 A2 그림은 화살이 한쪽으로 몰려있어 정확도는 낮으나 화살의 분포가 매우 좁아 상대적으로 정밀도는 높습니다.
B1 그림은 화살이 대체적으로 중앙 부분에 몰려 있어 정확도는 높으나 그 분포가 넓어 정밀도는 낮습니다. 아울러 B2 그림은 화살이 중앙 부분에 몰려있어 정확도가 높고 그 분포도 매우 좁아 정밀도도 높습니다.
이상으로 정확도와 정밀도에 대한 포괄적 개념을 알아봤습니다. 그러나 개념은 개념일 뿐 우리가 어떠한 물리량을 측정해서 측정값을 얻었을 때 그 값들의 정확도와 정밀도를 수치로 표현할 수 있어야 되겠죠.
우선 참값이 12.85 kg인 어느 물체의 질량을 여러분들이 직접 제작한 저울로 측정했다고 생각해보세요. 그 결과 다음과 같은 측정값들이 얻어졌습니다. 측정값의 단위는 kg입니다만 표기를 생략하도록 하겠습니다.
11.25, 12.78, 14.24, 12.92, 13.65, 11.86
총 6번을 측정했으며 약간씩 값들의 차이가 있습니다. 이 값들에 대한 정확도와 정밀도를 계산하고 표기하는 방법을 더 알아보겠습니다.
3. 측정 값의 정확도 계산과 표기
정확도를 표기하는 방법은 크게 2가지 방법이 있습니다.
첫번째는 평균값과 참값의 비율로 제시하는 방법입니다.
두번째는 오차를 제시하는 것입니다.
3-1. 평균값과 참값의 비율을 통한 정확도 계산과 표기
평균값과 참값의 비율을 통해 정확도를 계산하고 표기할 수 있습니다.
이를 위해 우선 아래의 (1)식으로 측정값들의 산술 평균 \mu을 구합니다. 여기서 x는 측정값이고, n은 측정 횟수입니다.
\tag{1}
\begin{align}
\mu &= {{\Sigma{x}}\over{n}}\\[10pt]
&= {{11.25+12.78+14.24+12.92+13.65+11.86}\over{6}}\\[10pt]
&=12.78~\mathrm{kg}
\end{align}정확도는 아래의 (2)식으로 계산합니다. 여기서 X는 참값을 뜻합니다.
\tag{2}
\begin{align}
정확도(\%) &= {{평균값}\over{참값}} \times 100 \\[10pt]
&= {{\mu}\over{X}} \times 100 \\[10pt]
&= {{12.78~\mathrm{kg}}\over{12.85 ~\mathrm{kg}}} \times 100 \\[10pt]
&= 99.46~\%
\end{align}따라서 ‘측정값들의 평균은 12.78 kg으로 참값 12.85 kg과 99.46%의 정확도를 갖습니다’라고 표기하면 됩니다. 100%에 가까울수록 정확도가 높습니다.
3-2. 오차를 이용한 정확도 계산과 표기
오차는 절대오차(absolute error)와 상대오차(relative error)가 있습니다. 이 두 양은 모두 정확도와 관련이 있습니다.
– 절대오차
절대오차 \epsilon란 측정값을 x, 참값을 X라 했을 때 아래 (3)식과 같이 그 두 값의 차이를 말합니다.
\tag{3}
\begin{align}
\epsilon &= x - X \\[10pt]
&= 11.25~\mathrm{kg} - 12.85~\mathrm{kg}\\[10pt]
&=-1.60 ~\mathrm{kg}
\end{align}따라서 ‘측정값 11.25 kg은 참값 12.85 kg과 -1.60 kg의 절대오차를 갖습니다’라고 표기하면 됩니다. 절대오차가 0에 가까울수록 정확도가 높습니다.
물론 모든 측정값들에 대해 각각 절대오차를 구한 후 그 절대오차들의 평균을 총 정확도로 제시할 수도 있을 것입니다.
– 상대오차
상대오차란 보통 백분율오차로 불리기도 합니다. 아래 (4)식으로 주어집니다.
\tag{4}
\begin{align}
백분율오차{\%} &= {{{\mid절대오차\mid}\over{참값}}} \times 100 \\[10pt]
&= {{\mid \epsilon\mid}\over{X}} \times 100 \\[10pt]
&={{1.60}\over{12.85}} \times 100\\[10pt]
&=12.45~\%
\end{align}따라서 ‘측정값 11.25 kg은 참값 12.85 kg과 12.45%의 상대오차를 갖습니다’라고 표기하면 됩니다. 상대오차가 0에 가까울수록 정확도가 높습니다.
물론 모든 측정값들에 대해 상대오차를 구한 후 그 상대오차들의 평균을 총 정확도로 제시할 수도 있을 것입니다.
3-3. 표준 오차를 이용한 정확도 계산과 표기
표준 오차를 이용하여 정확도를 표기하는 것은 아주 중요합니다. 또한 표준오차는 다양한 분야에서 활용되는데요.
이에 대해서는 내용이 많아 별도로 포스팅합니다. 아래의 링크를 클릭해 주세요.
4. 측정 값의 정밀도 계산과 표기
측정 값의 정밀도는 상대표준편차로 제시하는 방법이 있습니다. 아울러 측정값을 제시할 때 데이터의 평균값과 정밀도를 함께 표기하는 방법도 있습니다
4-1. 상대표준편차 (%RSD)를 이용한 정밀도 계산과 표기
상대표준편차 즉, %RSD(Relative Standard Deviation)는 측정 값들의 표준편차와 평균의 비율입니다.
상대표준편차를 계산하기 위해 필요한 편차(deviation), 표준편차(standard deviation)를 먼저 알아보겠습니다.
– 편차
편차란 측정값에서 측정값의 평균값을 뺀 값입니다. 측정값이 평균으로부터 멀리 떨어져 있을 수록 편차가 커져 정밀도가 나빠지는 것입니다.
\tag{5}
d = x-\mu– 표준편차
표준편차는 측정값의 퍼짐정도를 나타내는 수치입니다. 표준편차에는 2가지 종류가 있습니다. 하나는 모집단 표준편차이고 다른 하나는 표본 표준편차입니다.
모집단 전체로부터 데이터를 획득한경우 모집단 표준편차를 사용하고 모집단의 표본으로부터 데이터를 획득한 경우에는 표본 표준편차를 사용합니다. 표본 표준편차가 더 일반적입니다.
이때 측정 값을 x, 측정 값의 평균을 \mu, 측정 횟수를 n이라 하겠습니다.
[모집단 표준편차]
\tag{6}
\sigma = \sqrt{{\Sigma (d)^2}\over{n}} = \sqrt{{\Sigma(x-\mu)^2}\over{n}}
[표본 표준편차]
\tag{7}
s = \sqrt{{\Sigma (d)^2}\over{n-1}} = \sqrt{{\Sigma(x-\mu)^2}\over{n-1}}
위에서 제시한 데이터를 기준으로 표본 표준편차를 계산하면 다음과 같습니다. 표현이 반복되는 구간은 식을 일부 생략하였습니다.
\tag{8}
\begin{align}
s &= \sqrt{{(11.25-12.78)^2 + \ldots + (11.86-12.78)^2}\over{6-1}} \\[10pt]
&= 1.10
\end{align}– 상대표준편차, %RSD
이제 정밀도를 표현하는 상대표준편차를 정의하겠습니다. 상대표준편차, %RSD는 다음 (9)식과 같습니다.
\tag{9}
\begin{align}
\% \mathrm{RSD} &= {{표준편차}\over{평균}} \times 100 = {{\sigma}\over{\mu}} \times 100 \\[10pt]
&= {{1.10}\over{12.78}} \times 100 \\[10pt]
&=8.61 ~\%
\end{align}따라서 ‘측정값들의 정밀도를 나타내는 상대표준편차는 8.61 %입니다’라고 표기하면 됩니다. 상대표준편차가 작을수록 정밀도가 높습니다.
4-2. 측정 값의 범위를 이용한 정밀도 계산과 표기
대표 측정값을 제시할 때 ‘평균값 \pm정밀도’ 형식으로 표기하는 것이 일반적입니다.
이때 측정값의 범위(range)를 이용한 정밀도 표기 방법입니다.
여기서 x(\mathrm{max})는 측정 값 중 최대값을, x(\mathrm{min})은 측정 값 중 최소값을 의미합니다.
\tag{10}
\begin{align}
Range &= x(\mathrm{max}) - x(\mathrm{min}) \\[10pt]
&=14.24 - 11.25 \\[10pt]
&=2.99
\end{align}따라서 ‘측정값은 12.78\pm2.99 kg이며 정밀도는 최대값과 최소값의 범위값으로 구했습니다’라고 표기하면 됩니다.
4-3. 평균편차를 이용한 정밀도 계산과 표기
대표 측정값을 제시할 때 ‘평균값\pm정밀도’ 형식으로 표기하는 것이 일반적입니다. 이때 평균편차(Average deviation)를 이용한 정밀도 표기 방법입니다.
\tag{11}
\begin{align}
\bar d &= {{\Sigma|x-\mu |}\over{n}} \\[10pt]
&= {{1.53+0+1.46+0.14+0.87+0.92}\over{6}} \\[10pt]
&=0.82
\end{align}따라서 ‘측정값은 12.78\pm0.82 kg이며 정밀도는 평균편차로 구했습니다’라고 표기하면 됩니다.
4-4. 표준편차를 이용한 정밀도 계산과 표기
대표 측정값을 제시할 때 ‘평균값\pm정밀도’ 형식으로 표기하는 것이 일반적입니다. 이때 표준편차(Standard deviation)를 이용한 정밀도 표기 방법입니다.
위에서 표본 표준편차 s는 1.10으로 구했습니다.
따라서 ‘측정값은 12.78\pm1.10 kg이며 정밀도는 표준편차로 구했습니다’라고 표기하면 됩니다.
5. 측정 분야에서의 정확도와 정밀도에 대한 요약
- 정확도는 측정 값들이 한쪽으로 몰리는 일이 적은 정도를 나타낸다.
- 정밀도는 측정 값들의 퍼짐이 좁은 정도를 나타낸다.
- 정확도는 평균값과 참값의 비율, 절대오차, 상대오차, 표준오차를 이용해 계산하고 표기한다.
- 정밀도는 상대표준편차, 측정값 범위, 평균편차, 표준편차를 이용해 계산하고 표기한다.
6 thoughts on “측정 – 정확도와 정밀도의 개념, 계산, 표기 방법”