Last Updated on 2025-01-14 by BallPen
전기쌍극자의 등전위면과 전기장 모양을 매스매티카로 그려 봐요.
전기쌍극자 등전위면과 전기장 모양을 매스매티카(mathematica)로 그려볼 거에요. 이 글을 보시기 전에 전기쌍극자의 전위와 전기장에 관한 내용이 궁금하다면 이전 글을 참고하시기 바랍니다.
전기쌍극자의 전위는 다음과 같습니다.
\tag{D1}
\begin{align}
V = k{{\vec p \cdot \hat r }\over{r^2}}
\end{align}이 식을 시작으로 전기쌍극자의 등전위면과 전기장의 모양을 그려볼거에요.
아래는 이번 글의 목차입니다.
Contents
이 글에서 사용된 그림은 키노트로 작성되었습니다. 그림파일이 필요하신 분은 다운받아 사용하세요. dipole_electric_potential_field.key
1. 전기쌍극자의 전위
아래 [그림 1]에 전기쌍극자가 있어요.
![[그림 1] 전기쌍극자로부터 <span class="katex-eq" data-katex-display="false">\vec r</span>만큼 떨어진 점 <span class="katex-eq" data-katex-display="false">\rm A</span>](https://ballpen.blog/wp-content/uploads/2025/01/Untitled-2-1024x585.jpg)
전기쌍극자로부터 \vec r만큼 떨어진 점 \rm A의 전위는 다음 식과 같이 주어집니다.
\tag{1}
\begin{align}
V = k{{\vec p \cdot \hat r }\over{r^2}}
\end{align}여기서 k={1/{4 \pi \epsilon_0}}이며, \vec p는 전기쌍극자의 쌍극자모멘트, \hat r은 \vec r의 단위벡터로서 크기가 1인 벡터입니다.
(1)식에서 스칼라곱 \vec p \cdot \hat r을 풀어 쓰면 다음과 같이 쓸 수 있어요. 이 식에서 \theta는 쌍극자모멘트 \vec p와 단위벡터 \hat r사이의 사이각을 뜻합니다.
\tag{2}
\begin{align}
V = k{{p \cos \theta }\over{r^2}}
\end{align}그럼 이제부터 매스매티카를 이용해 (2)식부터 시작해서 전기쌍극자의 등전위면과 전기장 모양을 그려 볼게요.
2. 전기쌍극자의 등전위면과 전기장
2-1. 구면좌표계에서의 전위와 전기장
(2)식을 매스매티카에서 함수로 정의하고 변수 V_s로 치환합니다. 이때 아래첨자 \rm s는 구면좌표계의 spherical을 뜻합니다. 그리고 (2)식의 k는 계산의 편리성을 위해 1로 처리하도록 하겠습니다.
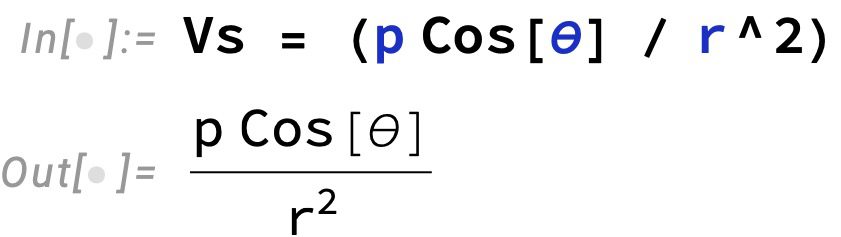
전기장은 전위의 기울기로부터 구할 수 있어요. 즉 \vec E = -\nabla V_s를 적용합니다. 물론 구면좌표계의 기울기 연산을 해야 해요.
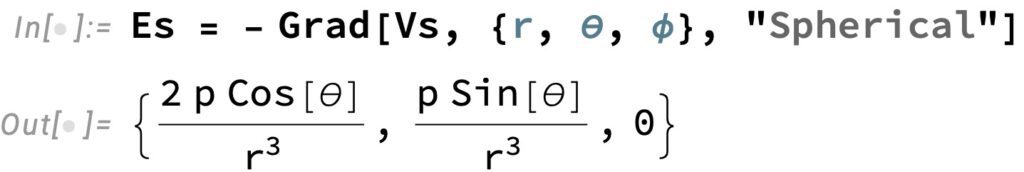
위 결과와 같이 구면좌표계의 r,~\theta,~\phi 방향에 따라 전기장의 크기가 각각 구해졌어요.
2-2. 구면좌표계에서의 전위와 전기장을 직각좌표계로 변환
이제 위 식을 통해 등전위면과 전기장을 구하면 되는데요. 이를 위해서는 구면좌표계의 V_s를 직각좌표계의 V_c로 변환해야 합니다.

여기서도 계산의 편리를 위해 쌍극자모멘트 p의 크기를 1로 처리했어요.
같은 방식으로 구면좌표계에서의 전기장 E_s를 직각좌표계의 E_c로 변환합니다.

2-3. 직각좌표계에서의 등전위면과 전기장
다음은 -50 V, -5 V, -1 V, 0 V, 1 V, 5 V, 50 V에 대한 등전위면을 구하기 위해 다음과 같이 코드를 작성했어요.

또한 전기장을 3차원공간에서 벡터로 표현하기 위해 다음의 코드를 작성했습니다.
그리고 위에서 만들어진 등전위선과 전기장을 함께 보여주기 위해 다음의 Show 명령어를 사용했어요.

그 결과 다음과 같이 전기쌍극자의 등전위면과 전기장 이미지가 출력됩니다.
![[그림 2] 전기쌍극자의 등전위면과 전기장](https://ballpen.blog/wp-content/uploads/2025/01/코드5-1024x874.jpg)
[그림 2]를 보면 중심의 평면을 기준으로 위쪽과 아래쪽에 동글 동글한 등전위면들이 대칭적으로 겹쳐져 있음을 알 수 있어요.
가장 작은 등전위면은 \pm 50~\rm V이고, 그 다음 큰 등전위면은 \pm 5~\rm V, 가장 큰 등전위면은 \pm 1~\rm V을 뜻해요. 그리고 중심의 평면은 0~\rm V의 등전위면을 뜻합니다.
또한 화살표로 표현된 것이 전기장 벡터입니다. [그림 2]에서 위쪽이 전기쌍극자의 양전하이고 아래쪽이 음전하에요.
그래서 전기장이 양전하에서 나가고 음전하로 들어가는 것을 볼 수 있습니다.
보다 명확한 전기장 벡터를 보기 위해 y=0 평면에서 전기장 벡터를 그려볼게요. 다음의 코드를 사용했어요.

그 결과 다음의 이미지를 관찰할 수 있습니다.
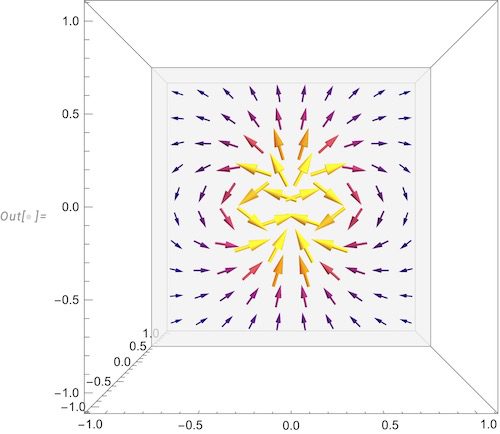
![[그림 3] 전기쌍극자의 전기장 벡터. 중심 위쪽이 양전하, 아래쪽이 음전하에 대응합니다.](https://ballpen.blog/wp-content/uploads/2025/01/코드6-1024x890.jpg)
[그림 3]은 [그림 2]의 중심 부분을 수직으로 잘라냈을 때 관찰되는 전기장 벡터에요.
전기장은 양전하에서 나오고 음전하로 들어가므로 [그림 2]의 중심부보다 약간 위쪽이 양전하가 있는 곳이고 중심부보다 약간 아래쪽은 음전하가 있는 곳이에요.