등가소음도 계산 방법 알려 드립니다. 음압레벨도 함께 공부해요.

Last Updated on 2024-02-21 by BallPen

등가소음도에 대한 이론적 전개와 관련 예제를 풀어보겠습니다.

1. 소음도의 크기와 대표 장소

아래의 표는 대표 장소별 등가소음도 크기를 제시하고 있습니다. 수치가 클수록 시끄러운 소리로 보시면 됩니다.

2. 등가소음도 심화 내용

2-1. 진동과 소음

우리 주변에는 수많은 진동원들이 있습니다. 비행기가 날아갈 때, 위 층에서 누군가가 쿵쿵 거릴 때, 자동차가 도로를 달릴 때, 기계가 돌아갈 때 등 진동을 만드는 원인은 무척 많습니다.

그러한 진동들이 사람 귀에 들리게 될 때 우리는 소음이라는 일반적인 명칭을 사용합니다. 물론 그 진동들이 주변 공기를 진동시키고, 진동된 공기가 사람 귀의 고막을 진동시킴으로서 소음을 느끼게 되는 것이죠.

그런데 이러한 소음은 근래 들어 매우 중요해졌습니다. 아파트 층간소음, 공항이나 도로변의 주택가 등에서 지나친 소음으로 인해 스트레스를 받는 경우가 발생하기 때문입니다.

따라서 소음으로 인한 피해 파악, 보상 논의, 소음 저감 방안 수립 등을 위해 소음도와 등가소음도를 측정하고 분석하는 것은 매우 중요한 절차가 될 것입니다.

그럼 등가소음도를 알아볼까요. 우선 이를 위해서는 음압레벨부터 알아야 합니다.

2-2. 음압레벨 (SPL: Sound Pressure Level)

일반적으로 물리학에서는 데시벨 (dB) 단위를 갖는 소음도 또는 소리준위 또는 음압레벨 L_\mathrm{a}를 다음과 같이 정의 합니다.

\tag{1}
L_\mathrm{a} = 10 \log {{I}\over{I_0}}

여기서 I는 측정 대상 소리의 세기(intensity)이고, I_0는 기준 세기로서 인간이 들을 수 있는 가청 문턱값(I_0 =1.00 \times 10^{-12}\mathrm{W/m^2})을 의미합니다.

반면에 공학에서는 소리 세기 대신에 압력 진폭(pressure amplitude)을 사용하여 음압레벨을 표현합니다. 그러면 위의 공식이 다음과 같이 달라집니다.

\tag{2}
L_\mathrm{a} = 10 \log {{p^2}\over{p_0^2}}

여기에서 p는 측정 대상 소음에 대한 압력 진폭의 실효값이고, p_0는 기준 압력 진폭의 실효값으로서 p_0 = 20~ \mu \mathrm{Pa} = 20 ~\mu \mathrm{N/m^2}에 해당합니다.

소리 세기 I와 압력 진폭의 최대값 \Delta P_{\mathrm{max}} 사이의 관계식이 궁금한가요? 바로 다음과 같이 주어집니다. 아래 식이 유도되는 과정은 여기를 참고하세요.

\tag{3}
I = {{(\Delta P_{\mathrm{max}})^2}\over{2 \sigma v}}

여기서 \sigma는 공기의 밀도이고 v는 소리의 속력입니다.

그렇다면 소리세기의 문턱값 I_0 =1.00 \times 10^{-12}\mathrm{W/m^2}가 압력 진폭으로 p_0 = 20~ \mu \mathrm{Pa}에 어떻게 대응하는 지를 계산해 보겠습니다.

\tag{4}
\begin{align}
I_0 &= {{(\Delta P_{0\mathrm{max}})^2}\over{2 \sigma v}} \\[10pt]
{1.00 \times 10^{-12} \mathrm{W/m^2}}&= {{(\Delta P_{0\mathrm{max}})^2}\over{2 \times 1.293 \mathrm{kg/m^3} \times 331\mathrm{m/s}}} \\[10pt]
\Delta P_{0\mathrm{max}} &= 29.256 \mu \mathrm{Pa}\\[10pt]
\end{align}

압력 진폭의 최대값 \Delta P_{0 \mathrm{max}}는 압력진폭의 실효값 p_0와 다음의 관계가 있습니다.

\tag{5}
p_0 = {{\Delta P_\mathrm{0max}}\over{\sqrt{2}}} =  {{29.256 \mu \mathrm{Pa}}\over{\sqrt{2}}}  \approx 20 \mu \mathrm{pa}

2-3. 등가소음도 (Equivalent Noise Level) 정의

이제 등가소음도를 알아보겠습니다.

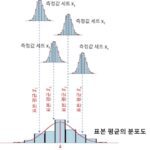
등가소음도란 소음도 즉, 음압레벨이 시간에 따라 변할 경우(통상적으로 당연히 변하게 됨), 측정시간 내에서 이와 동등한 평균 음압레벨을 주는 연속 정상음으로 환산하였을 때의 소음도가 되겠습니다. 기호로는 보통 음압레벨 L_\mathrm{a}와 구분하기 위해 L_\mathrm{eq}로 표기합니다.

등가소음도는 음압레벨의 식에서 평균의 개념을 반영하여 다음과 같이 정의합니다.

\tag{6}
\begin{align}
L_\mathrm{eq} = 10 \log \Big( {{1}\over{T}} \int_0^T {{I}\over{I_0}} dt  \Big)
\end{align}

위 식에서 괄호안은 시간 T동안 변화된 {{I}\over{I_0}}의 평균 값을 뜻합니다. 이 식을 위에서 설명한 I와 p사이의 관계식을 이용하여 조금만 변형해보겠습니다.

\tag{7}
\begin{align}
L_\mathrm{eq} &= 10 \log \Big( {{1}\over{T}} \int_0^T {{{{(\Delta P_{\mathrm{max}})^2}\over{2 \sigma v}}}\over{         {{{(\Delta P_{0{\mathrm{max}}} )^2}\over{2 \sigma v}} }         }} dt  \Big) \\[10pt]
&= 10 \log \Big( {{1}\over{T}} \int_0^T {{{{(\Delta P_{\mathrm{max}})^2}\over{ (\sqrt{2})^2    }}}\over{         {{{(\Delta P_{0{\mathrm{max}}} )^2}\over{ (\sqrt{2})^2      }} }         }} dt  \Big) \\[10pt]
&= 10 \log \Big({{1}\over{T}} \int_0^T   {{{p}^2}\over{{p_0}^2}}    dt  \Big)\\
\end{align}

위식에서 \sigma와 v는 약분되어 사라진것이고요. p= {{\Delta P_{\mathrm{max}}}\over{\sqrt{2}}}의 관계를 이용한 것입니다. 다시 말씀드리면 여기서 p는 압력진폭의 실효값이며, p_0 = 20 \mu \mathrm{Pa}입니다.

실용적인 경우 압력진폭을 측정하여 위 식을 통해 등가소음도를 구하기 보다는, 소음계를 통해 소음도, 즉 음압레벨을 일정 시간동안 측정하고 이를 기반으로 등가소음도를 구하는 경우가 일반적입니다. 이때 사용하는 식은 아래와 같습니다.

\tag{8}
L_{\mathrm{eq}} = 10 \log \Big(         {{1}\over{100}}  \sum  P_{\mathrm{i}} 10^{L_{\mathrm{ai}}\over{10}    }       \Big) 

여기서 P_{\mathrm{i}}는 전체 측정시간 대비 i번째 소음에 대한 측정시간의 백분율이고, L_{\mathrm{ai}}는 i번째 소음의 중간 시간에서의 음압레벨입니다.

이 식으로도 L_{\mathrm{eq}}가 올바르게 계산되는지 보겠습니다. 만약 어떤 기계음에 대해 소음계로 15분동안 음압레벨을 측정했는데 20 dB이 일정하게 나왔다고 보겠습니다. 15분 동안 음압레벨이 변하지 않았으니 당연히 L_{\mathrm{eq}}도 20 dB이 나와야 합니다. 계산해보겠습니다.

\tag{9}
\begin{align}
L_{\mathrm{eq}} &= 10 \log \Big( {{1}\over{100}} \sum P_{\mathrm{i}} 10^{{L_{\mathrm{ai}}}\over{10}} \Big) \\[10pt]
&= 10 \log \Big( {{1}\over{100}} \big( {{15}\over{15}} \times 100 \big) 10^{{20 \mathrm{dB}}\over{10}} \Big) \\[10pt]
&=10 \log 10^{{20}\over{10}}\\[10pt]
&=10 \log 100\\[10pt]
&=20~{\mathrm{dB}}
\end{align}

20 dB이 잘 나오는 것을 볼 수 있습니다. 예제 하나 풀어보고 등가소음도 설명 마무리하겠습니다.

3. 등가소음도 계산 예제

(문제) 어떤 공장 지대에서 30 min 동안 연속해서 소음도, 즉 음압레벨을 측정했는데 70 dB이 20 min, 75 dB이 10 min동안 측정되었다면 등가소음도는 얼마인가?

\tag{10}
\begin{align}
L_{\mathrm{eq}} &= 10 \log \Big( {{1}\over{100}} \sum P_{\mathrm{i}} 10^{{L_{\mathrm{ai}}}\over{10}} \Big) \\[10pt]
&= 10 \log  \Big( {{1}\over{100}} \big(   {{20\mathrm{min}}\over{30\mathrm{min}}} \times 100 \times 10^{{70\mathrm{dB}}\over{10}} + {{10\mathrm{min}}\over{30\mathrm{min}}} \times 100 \times 10^{{75\mathrm{dB}}\over{10}}  \big) \Big)\\[10pt]
&= 10 \log \Big( {{1}\over{30}} \big( 20 \times 10^{7} + 10 \times10^{7.5} \big) \Big)\\[10pt]
&= 10 \Big[ \log \big( 20 \times 10^7 + 10 \times 10^{7.5} \big) - \log 30 \Big]\\[10pt]
&=10(8.713 - 1.477)\\[10pt]
&= 72.36 ~\mathrm{dB}
\end{align}

4. 음압레벨 및 등가소음도 관련 연습문제

아래에 추가적인 문제가 있으니 음압레벨 및 등가소음도 개념 이해에 참고하시기 바랍니다. 잘 아시겠지만 개념이해에는 문제풀이가 제일 좋습니다.

• 음압 레벨을 구한 후 등가소음도를 도출하는 문제
• 소음도(음압레벨)를 가산(덧셈)과 감산(뺄셈)하는 연습문제
• 소음의 거리감쇠 공식 유도와 예제 풀이

ilovemyage 추천 글

• 기름 차에 쓰여진 취급량과 적재량으로 밀도를 구해볼까요

Related posts.

소음도 가산과 감산 연습 문제 등가소음도 연습 문제 소음의 거리감쇠 공식 유도와 예제 풀이 자동차 배기량(displacement)의 정의와 어떻게 계산하는지를 알아볼까요? 단위 표기 오류가 있는 도쿄 올림픽 중계방송이 불편한 이유 질량과 무게 – 전자 저울로 측정한 값은 질량일까요 무게일까요? 가속도 운동 – 음의 가속도, 0의 가속도, 양의 가속도 개념 정리 벡터, 벡터의 작도, 벡터의 크기, 벡터의 성분