BallPen.blog, 내 나이의 빛깔
독립 및 종속 변수에 의존하는 다양한 함수의 미분 방법을 알아봐요. 함수의 미분 방법을 설명드립니다. 어떤 함수가 독립 및 종속 변수에 의존하는 경우 미분을 어떻게 하느냐에 관한 이야기에요. 예를 들어 독립변수를 와 라고 할 때 아래 함수들을 보면 독립변수에만 의존하는 경우도 있고 독립변수 뿐만아니라 종속변수에도 의존하는 경우도 있음을 알 수 있어요. 이 경우 어떻게 미분하면 될까요? … Read more
함수를 적분 후 미분한 것과 미분 후 적분한 것의 결과가 같은지 알아 봐요. 어떤 함수를 적분 후 미분 또는 미분 후 적분한 결과가 같은지 궁금한 경우가 있어요. 특히 과학이나 공학 분야에서 이런 경우가 간혹 나오게 되는데요. 그 결과는 아래와 같습니다. 상수를 적분구간으로 하는 다변수함수에 대해서는 적분과 미분의 순서가 바뀌어도 같다는 것을 알 수 있어요. 아래는 … Read more
전치행렬을 만드는 방법과 그 성질을 알아 봐요. 전치행렬(Transpose Matrix)이란 어떤 행렬의 행과 열을 맞바꾼 행렬을 뜻합니다. 이를 기호로 쓰면 어떤 행렬 의 전치행렬은 로 표기합니다. 예를 들어 다음의 행렬 에 대한 전치행렬 는 다음과 같아요. 전치행렬은 직교 대각화 문제(행렬의 대각화 조건), 직교행렬등을 이해하는데 반드시 필요한 개념입니다. 이번 글에서는 전치행렬이 어떻게 정의되며 그 성질이 무엇인지 알아보겠습니다. … Read more
행렬의 대각화 개념에 대해 알아 봐요. 행렬의 대각화(diagonalization of matrices)란 대칭 선형 변환 행렬 에 고유벡터로 구성된 직교행렬 을 아래 식과 같이 적용하면, 고유값 로 구성된 대각행렬 가 얻어지는 것을 말합니다. 이 글에서는 위 (D1)식이 어떻게 유도되고, 행렬의 대각화 의미와 예제를 풀어보겠습니다. 아래는 이번 글의 목차입니다. Contents1. 고유값 문제 복습2. 행렬의 대각화2-1. 행렬의 대각화를 하는 … Read more
행렬의 고유값, 고유벡터를 구하는 방법과 그 의미를 알아봐요. 고유값 문제(eigenvalue problem)란 어떤 입력 벡터 를 정방행렬 로 변환했을 때 결과 벡터가 입력 벡터 의 실수배 를 만족하는 경우, 를 행렬 의 고유값, 를 에 대응하는 고유벡터라고 합니다. 이를 식으로 표현하면 다음과 같아요. 고유값 문제란 위 식을 만족하는 고유값 와 고유벡터 를 구하는 구하는 것을 말해요. … Read more
직교행렬과 그 성질을 알아봐요. 직교행렬(orthogonal matrix)이란 역행렬과 전치행렬이 같은 정방행렬을 말합니다. 기호로 표현하면 행렬 를 직교행렬이라 할 때 다음 관계가 성립한다는 거에요. 여기서 는 행렬 의 전치행렬, 는 역행렬을 뜻해요. 이번 글에서는 직교행렬 및 그 성질에 대해 알아봅니다. 본문 그림 작성에 사용된 키노트 파일은 아래 링크에서 다운받을 수 있어요. 키노트 그림 파일: orthogonal_matrix.key Contents1. 복습1-1. … Read more
역행렬이 어떻게 정의되고, 또 그 성질은 어떤지 알아봐요. 역행렬(inverse matrix)이란 어떤 정방행렬에 곱했을 때 단위행렬을 만들어내는 행렬을 말합니다. 즉, 행과 열이 같은 어떤 정방행렬 가 있을 때 이 정방행렬의 앞 또는 뒤에 의 역행렬 을 곱해주면 단위 행렬 가 만들어져요. 그러면 역행렬 은 어떻게 만들 수 있을까요? 결론부터 말씀드리면 다음과 같아요. 여기서 는 행렬 의 … Read more
행렬식을 여인수 전개로 표현하는 방법을 알아봐요. 여인수 전개(cofactor expansion)란 행렬식(determinant)을 여인수로 전개하여 표현한 것을 말해요. 여인수 전개는 라플라스 전개(Laplace expansion)라고도 불립니다. 이때 여인수(cofactor)의 뜻이 궁금할 텐데요. ‘나머지에서 도출된 수’라는 뜻의 한자어로 행렬 일부를 제외한 나머지 부분에서 도출된 숫자 임을 의미합니다. ‘어른 여자’를 뜻하는 ‘여인’과는 무관해요. 결론부터 말씀드리면 3×3 행렬의 행렬식을 여인수 전개하면 다음과 같아요. 여인수 … Read more
연립 1차 방정식을 푸는데 사용되는 크래머 공식을 알아 봐요. 크래머 공식(Cramer’s rule)이란 1차 연립방정식을 행렬로 변환한 후 미지수 와 를 구하는 공식을 말합니다. 예를 들어 아래 왼쪽의 연립방정식을 행렬로 표현하면 오른쪽과 같아요. 이때 아래 식에서 붉은색 행렬을 행렬이라고 해봐요. 그리고 위 식에서 와 를 구하는 아래의 공식을 ‘크래머 공식’이라고 말합니다. 여기서 는 행렬의 행렬식(determinant)을 뜻해요. … Read more
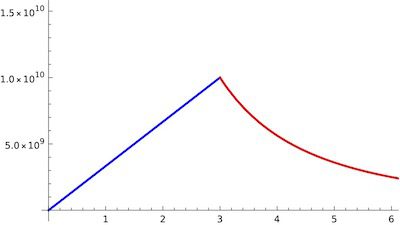
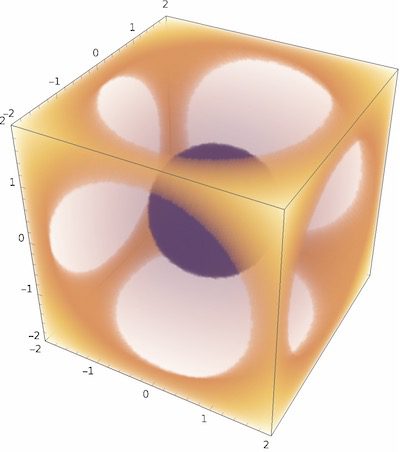
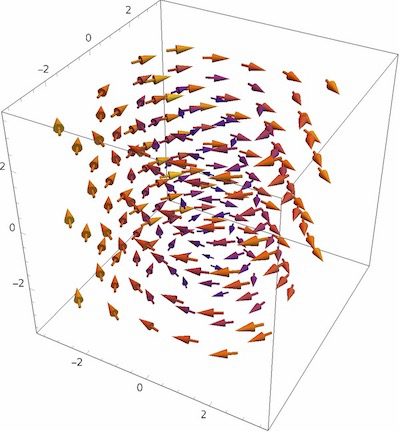
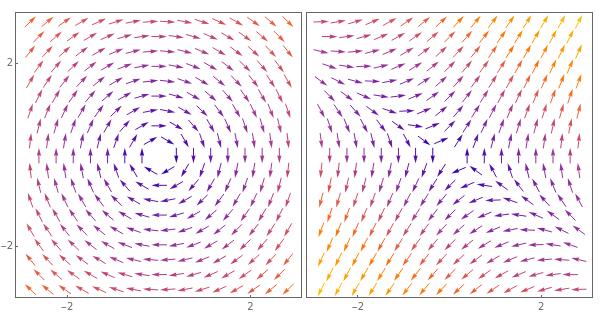
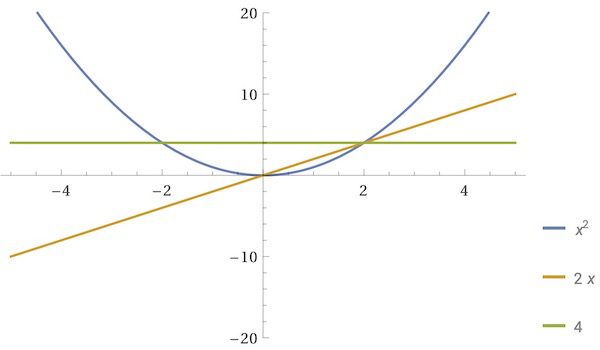
여러 개의 Plot 유형을 한 그래프에 합쳐서 나타내는 Show 명령어를 알아봐요. Show 명령어는 매스매티카에서 여러 개의 그래프를 합쳐 한 프레임의 그래프로 나타내는 명령어 입니다. 예를 들어 Plot과 ListPlot을 한 그래프에 그리고 싶을 때, DensityPlot과 ContourPlot을 한 그래프로 그리고 싶을 때 등 사용할 수 있는 유용한 기능이에요. 이번 글에서는 서로 다른 두 함수를 한 그래프에 구간을 … Read more